自动搬运

查看原文

来自洛谷，原作者为

	Danno0v0 我们会再次见面的，相信我。再见。

搬运于2025-08-24 21:52:23，当前版本为作者最后更新于2021-10-29 08:22:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Update 修改了错别字。

在做这道题前，建议先做 P2774 方格取数问题 和 P3355 骑士共存问题 以保证您会染色网络流。

一道染色题的究极形态。

首先看到方格想网络流。看到要欧拉掉点代价最小就可以想最小割了。最小割，又是在网格中，染色没跑了。

那么，我们进行黑白染色——

然后就会发现染完后什么用都没有。

难道是这道题不能用染色？

然后我们来看那四个老 C 不喜欢的图形，都是四个方块组成的。

而且——

我们发现，假如我们用四个颜色蓝绿红黄对这四个图形进行染色的话，就会发现，一定会存在这样一条路径：黄—蓝—特殊边—绿—红。

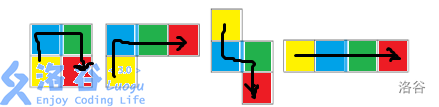
有一点网络流的味道了。

试想一下，假设我们按 源点—黄—蓝—特殊边—绿—红—汇点 连边的话，假若图还连通就说明还有这种图形。必须把这个图变成不连通然后花费最小代价，这不就是最小割吗。

那么现在问题就是如何连层与层的边以及边权的问题了。

这就很简单了。

我们刚刚说一个不喜欢图形中的路径是黄—蓝—特边—绿—红，那就说明每一个蓝点只能由黄点溜过来，每一个特殊边只能由蓝点流过来，后面几层同理，所以就向黄点周围所有蓝点连边，所有蓝点向特殊边连，后面几层同理。

那么边权呢？

如果把一个黄点欧拉掉了，那么周围所有蓝点就都不可以通过这个黄点组成讨厌图形了。蓝点欧拉掉了特殊边也就不能组成特殊图形了。一下几层同理。

说明边权不在黄—蓝，绿—红而在黄—源点，蓝—特边，绿—特边，红—汇点上。回推一下这也是符合题意的。把黄点与源点的边割掉了就说明不选这个黄点，它连的所有蓝点都不会通过它产生不喜欢图形。那么，我们把上述 $4$ 种边的边权改成欧拉这个方块的代价，其余边全是 INF 就好了。然后我们发现，蓝—特殊边—绿 这一条路径其实和 蓝—绿 然后边权为 $\min(val[Blue],val[Green])$ 是等价的（因为每条特殊边最多只有一个蓝点和绿点和它连边），这样就顺便把特殊边这一层给优化掉了。

那么就还剩最后一个问题了。怎么染色让这个图中不管不喜欢图形怎么摆都是按以上路径的？

这个吗没什么技巧，多试试几次就出来了。总之就是这样染色的：

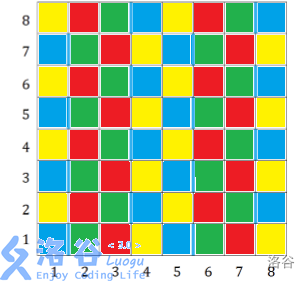
然后就会发现这个图的循环规律是每个 $2 \times 4$ 的长方形都是一样的，然后就对每一个长方形内八个不同格子进行特判就好了。

然后就是一些零零碎碎的问题：

第一个，怎么存每一个格子所建的节点。

按照以往的我们直接用列乘上 $10$ 的幂再加上行然后直接用数组存肯定是木大的，这个图很贴心的给出了长宽小于 $10^5$ ,所以不得不建一个 <long long,int> 的 map 来强行让每一个格子的坐标（按刚刚的方法把坐标处理成 long long ）与一个节点编号对应。

第二个，怎么比较快连边。

黄点和红点都是可以直接在读入时就直接向源汇连边的；蓝点和绿点在读入时记录一下然后读入完后再向周围的点连边好了。

code：（记住蓝点连边有两套不同方法，绿点连边也有两套不同方法，我为这个调了一个晚上）

#include<bits/stdc++.h>
#define maxx 2000001
#define B 1
#define G 2
#define R 3
#define Y 4
#define S 1999999
#define T 2000000
using namespace std;
map<long long,long long>check;
map<long long,long long>cost_;
long long r,c,n;
struct node
{
	long long col,val,x,y;
}N[maxx];
long long fi[maxx],nx[maxx],to[maxx],val[maxx],depth[maxx],tot=1,num,heroes[maxx],b_g;
long long dx[4]={-1,0,0,1};
long long dy[4]={0,1,-1,0};
void link(long long a,long long b,long long c)
{
	nx[++tot]=fi[a];
	fi[a]=tot;
	to[tot]=b;
	val[tot]=c;
}
bool bfs()
{
	memset(depth,0,sizeof(depth));
	queue<long long>que;
	que.push(S);
	depth[S]=1;
	while(!que.empty())
	{
		long long x=que.front();
		que.pop();	
		for(long long i=fi[x];i;i=nx[i])
		{
			long long v=to[i];
			if(val[i]&&!depth[v])
			{
				depth[v]=depth[x]+1;
				que.push(v);
			}
		}
	}
	return depth[T];
}
long long dinic(long long x,long long in)
{
	if(x==T)
	{
		return in;
	}
	long long out=0;
	for(long long i=fi[x];i&&in;i=nx[i])
	{
		long long v=to[i];
		if(val[i]&&depth[x]+1==depth[v])
		{
			long long res=dinic(v,min(val[i],in));
			in-=res;
			out+=res;
			val[i]-=res;	
			val[i^1]+=res;
		}
	}
	if(out==0)
	{
		depth[x]=0;
	}
	return out;
}
signed main()
{
	cin>>c>>r>>n;
	for(long long i=1;i<=n;i++)
	{
		cin>>N[i].x>>N[i].y>>N[i].val;
		long long x=N[i].x;
		long long y=N[i].y;
		check[x*1000000+y]=++num;
		switch(x%4)
		{
			case 1:
				if(y%2==1)
				{
					N[i].col=B;
					heroes[++b_g]=i;	
				}
				else
				{
					N[i].col=Y;
					link(S,num,N[i].val);
					link(num,S,0);
				}
				break;
			case 2:
				if(y%2==1)
				{
					N[i].col=G;
					heroes[++b_g]=i;
					cost_[x*1000000+y]=N[i].val;
				}
				else
				{
					N[i].col=R;
					link(num,T,N[i].val);
					link(T,num,0);
				}
				break;
			case 3:
				if(y%2==1)
				{
					N[i].col=R;
					link(num,T,N[i].val);
					link(T,num,0);
				}
				else
				{
					N[i].col=G;
					heroes[++b_g]=i;
					cost_[x*1000000+y]=N[i].val;
				}
				break;
			case 0:
				if(y%2==1)
				{
					N[i].col=Y;
					link(S,num,N[i].val);
					link(num,S,0);
				}
				else
				{
					N[i].col=B;
					heroes[++b_g]=i;
				}
				break;
		}
	}
	for(long long i=1;i<=b_g;i++)
	{
		long long xx=N[heroes[i]].x;
		long long yy=N[heroes[i]].y;
		if(N[heroes[i]].col==B&&xx%4==0)
		{
			if(xx+dx[0]>=1&&xx+dx[0]<=c&&yy+dy[0]>=1&&yy+dy[0]<=r)
			{
				long long s=check[(xx+dx[0])*1000000+yy+dy[0]];
				if(s)
				{
					long long a=check[xx*1000000+yy];
					link(a,s,min(N[heroes[i]].val,cost_[(xx+dx[0])*1000000+yy+dy[0]]));
					link(s,a,0);
				}
			}
			for(long long i=1;i<4;i++)
			{
				if(xx+dx[i]>=1&&xx+dx[i]<=c&&yy+dy[i]>=1&&yy+dy[i]<=r&&check[(xx+dx[i])*1000000+yy+dy[i]])
				{
					long long a=check[(xx+dx[i])*1000000+yy+dy[i]],b=check[xx*1000000+yy];
					link(a,b,0x7ffffff);
					link(b,a,0);
				}
			}
		}
		else if(N[heroes[i]].col==B&&xx%4==1)
		{
			if(xx+dx[3]>=1&&xx+dx[3]<=c&&yy+dy[3]>=1&&yy+dy[3]<=r)
			{
				long long s=check[(xx+dx[3])*1000000+yy+dy[3]];
				if(s)
				{
					long long a=check[xx*1000000+yy];
					link(a,s,min(N[heroes[i]].val,cost_[(xx+dx[3])*1000000+yy+dy[3]]));
					link(s,a,0);
				}
			}
			for(long long i=0;i<3;i++)
			{
				if(xx+dx[i]>=1&&xx+dx[i]<=c&&yy+dy[i]>=1&&yy+dy[i]<=r&&check[(xx+dx[i])*1000000+yy+dy[i]])
				{
					long long a=check[(xx+dx[i])*1000000+yy+dy[i]],b=check[xx*1000000+yy];
					link(a,b,0x7ffffff);
					link(b,a,0);
				}
			}
		}
		else if(N[heroes[i]].col==G&&xx%4==2)
		{
			for(long long i=1;i<4;i++)
			{
				if(xx+dx[i]>=1&&xx+dx[i]<=c&&yy+dy[i]>=1&&yy+dy[i]<=r&&check[(xx+dx[i])*1000000+yy+dy[i]])
				{
					long long a=check[xx*1000000+yy],b=check[(xx+dx[i])*1000000+yy+dy[i]];
					link(a,b,0x7ffffff);
					link(b,a,0);
				}
			}
		}
		else
		{
			for(long long i=0;i<3;i++)
			{
				if(xx+dx[i]>=1&&xx+dx[i]<=c&&yy+dy[i]>=1&&yy+dy[i]<=r&&check[(xx+dx[i])*1000000+yy+dy[i]])
				{
					long long a=check[xx*1000000+yy],b=check[(xx+dx[i])*1000000+yy+dy[i]];
					link(a,b,0x7ffffff);
					link(b,a,0);
				}
			}
		}
	}
	long long ans=0;
	while(bfs())
	{
		ans+=dinic(S,0x7ffffff);
	}
	cout<<ans;
}

对了数据有点水你输出 $0$ 都能过掉 $5$ 个点