自动搬运

查看原文

来自洛谷，原作者为

	Tracy_Loght 爱与火的歌舞，命与情的交织，是遗憾的狂想最后一曲

搬运于2025-08-24 21:52:11，当前版本为作者最后更新于2024-07-02 17:02:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

又有又改了改，可以放心食用了，滑稽。

发现有些的方有些绕，请遇见了记得提醒我一下。

简单数学题，前置知识：一次函数，电脑。

思路：

注：侦察员位置的纵坐标的那一列统称为目标列。

先注意到什么，目标列是不变的，封锁区也是不变的，所以我们大可以开一个数组，只记录下目标列与封锁区上的点。

注意精度。

主要思路就上面的了。

一步步开始算，首先如何判断目标列与封锁区边的交点有什么。

肯定一次函数啊，但是不好玩的是目标列可能与封锁区的边重合。

得了，先算一次函数吧，不会的看这里：度娘。

int RFT(double x,double y,double x_,double y_,double m)//已知的两个点，m为目标列
{
	double k=0,b=1,k_=0,b_=1;
	double x1=x,y1=y;
	k=x*x_;y=y*x_;b=b*x_;
	k_=x_*x;y_=y_*x;b_=b_*x;
	b=(y_-y)/(b_-b);k=(y1-b)/x1;
	return k*m+b;
}

(假设只考虑有斜率的情况)。

然后具体一点，判断目标列上所有的点是否在封锁区内。

这个很好想，从最后一个与目标点的交点来看，它以前的到前一个与目标点的交点中一定要计算，然后一段不计算，一段计算，一段计算，一段不计算。

呃の解释不对头。

再解释一下，对于一个多边形，将其切片一下，然后转过来：

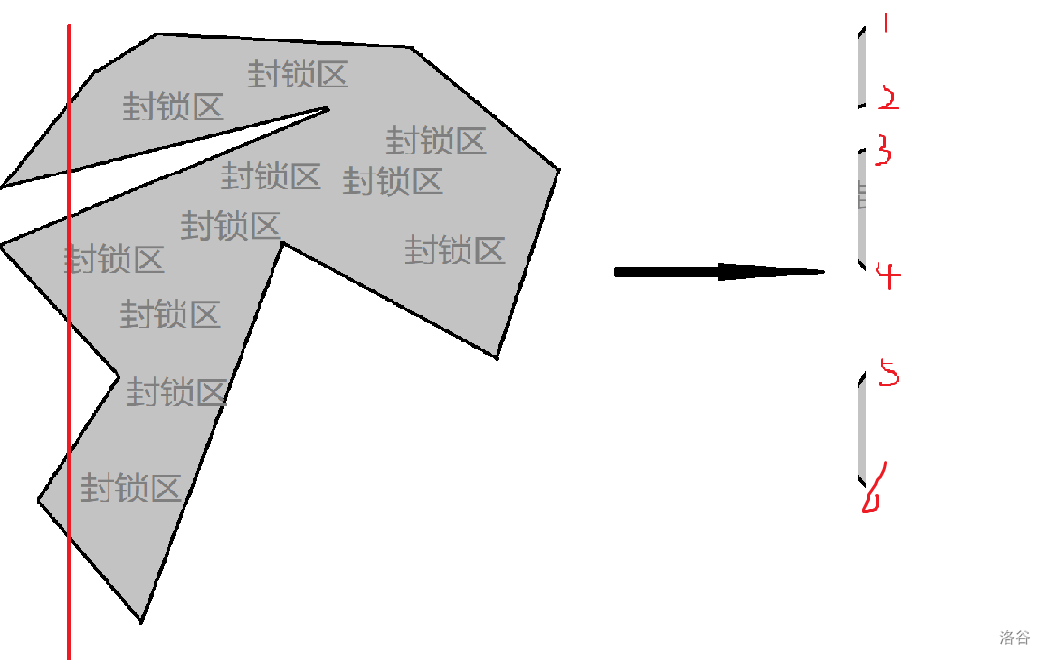
再对着每一个交点一看，从上到下编号，答案就是：

代码：

#include<bits/stdc++.h>
#define ft __float128   //我曾经一度怀疑过精度的问题
#define ld long double
using namespace std;
ft kl[10001],jl;
int ans,n,l,r;
struct {
	int x,y;
} o[51]; //储存每一个点
ft RFT(ft x,ft y,ft x_,ft y_,ft m) {   //已知的两个点的坐标，m 为目标列
	if(x>x_)swap(x,x_),swap(y,y_);     //在调用这个函数时，请保证这两点构成的直线经过直线 y=m
	if(y==y_) return y;
	else if(x==0) { //特判斜率 0 的情况
		ft k=0,b=1; //但是感觉没用 
		if(x_==0) return 0;
		else {
			b=y;
			k=(y_-b)/x_;
			return k*m+b;
		}
	} else {     //正常算
		ft k=0,b=1,k_=0,b_=1,x1=x,y1=y;//计算交点 
		k=x*x_; y=y*x_; b=b*x_;
		
		k_=x_*x; y_=y_*x; b_=b_*x;
		b=(y_-y)/(b_-b);
		k=(y1-b)/x1;
		return k*m+b;
	}
}
int main() {
	ios::sync_with_stdio(0);
	std::cin.tie(0);
	std::cout.tie(0);
	cin>>n;
	for(int i=1; i<=n; i++) cin>>o[i].x>>o[i].y;
	cin>>l>>r;
	o[0].x=o[n].x;//因为这个是一个多边形，要在首尾连边
	o[0].y=o[n].y;
	for(int i=1; i<=n; i++) {
		int il=min(o[i-1].x,o[i].x);
		int xr=max(o[i].x,o[i-1].x);
		if(o[i-1].x==l&&o[i].x!=l) kl[++ans]=o[i-1].y;   //对于每一种情况分点判断
		else if(o[i-1].x!=l&&o[i].x==l) kl[++ans]=o[i].y;
		else if(il<l&&l<xr) {
			ft as=RFT(o[i-1].x,o[i-1].y,o[i].x,o[i].y,l);
			kl[++ans]=as;
		}
	}
	std::sort(kl+1,kl+ans+1);
	for(int i=2; i<=ans+1; i+=2) { //计算在封锁区内的值
		if(kl[i]!=0) jl=jl+kl[i]-kl[i-1];
		//注意为空的情况，怎么来的就不知道了，太久了忘了 
	}
	int daan=jl/1;//朴素的去小数方式 
	cout<<daan;
	return 0;
}

点个赞呗。

过了哩，自认为非常好理解，但是代码不好写。