自动搬运

查看原文

来自洛谷，原作者为

	冒泡ioa **

搬运于2025-08-24 21:51:43，当前版本为作者最后更新于2018-12-19 17:25:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

安利下自己的博客 题目链接

首先这是一颗树。

这一题我们用贪心的方法来解决，首先来看看样例：

样例1很不友好，不如不给，显然我们可以经过3个点。

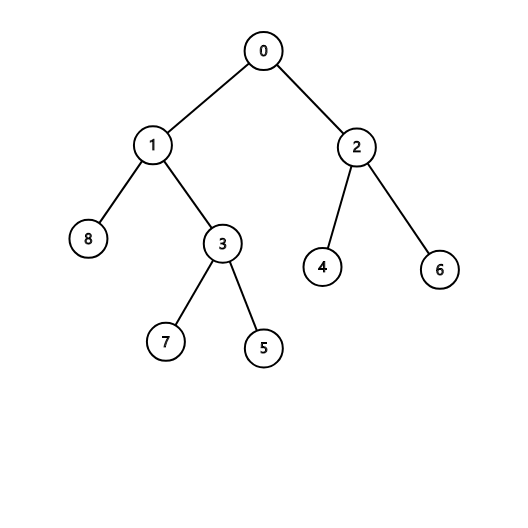
我们可以从样例2发现我们的贪心策略。

为了实现经过的点最多的这一条件，我们希望每次走一步都多走一个点，如果我们选择最长链的话，在链上每走一步就多走了一个点，如果走不完最长链，那答案就是步数+1，而如果走完最长链还有剩余步数的话，每两步可以多访问一个节点。

为什么剩余步数每两步可以多访问一个节点？

对于没有全访问的情况（如果这种方法求出来的值大于总数，则输出总数），最长链上肯定存在一条边连着一个没有访问的节点 ，当走到这里的时候，可以花两步去访问再回来。

为什么最长链是最优的？

显然，因为如果我们不走最长链的话，我们走任意其他的链对答案的贡献都没有最长链大，虽然剩下的剩余步数多，但是根据上面的推论，每两个剩余步数才有一个贡献，因此最长链是最优的。

讲得已经比较清楚了，有些细节没有提到，建议先自己写一遍再看代码！！

代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 103;
int Nt[MAXN<<1],Head[MAXN<<1],to[MAXN<<1],tot;
bool used[MAXN];
int n,m;
int mx=0;

void add(int a,int b){
	Nt[++tot]=Head[a];
	to[tot]=b;
	Head[a]=tot;
}	

void dfs(int pos,int dep){//最长链可以用深搜跑最大深度得到
	used[pos]=1;
    mx=max(mx,dep);
	for(int i=Head[pos];i;i=Nt[i]){
		int y=to[i];
		if(used[y])continue;
		dfs(y,dep+1);
	}
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);add(b,a);
	}
	dfs(0,1);
	if(m<=mx-1)printf("%d\n",m+1);//如果走不完最长链，那答案就是步数+1
	else printf("%d\n",min(n,mx+(m-mx+1)/2));
	return 0;
}