1 条题解
-
0
自动搬运
来自洛谷,原作者为

whiteqwq
寻找着梦与现实的交点 在哪呢 在哪呢搬运于
2025-08-24 21:51:13,当前版本为作者最后更新于2020-06-30 21:51:18,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
注意:“环套树”与“基环树”意思均为一棵树上增加一条边后形成的图,本文采取“基环树”的叙述方式。
题意
题意:给定 个点,每个点都会依赖另一个点,可以用一定的代价改变一个点依赖的点,求让依赖关系变为环的最小代价。
数据范围:。
分析
首先,我们可以将点之间的依赖关系看为边(被依赖的点连向依赖别的点的点),这样依赖关系组成的图就会成为一个基环树森林。(简单证明一下:因为每个点只依赖一个点,所以只会有一条入边,即每一个大小为 的森林至多有条边,即为一棵基环树)
为了将这张图最终变为一个环,我们可以把每一个基环树拆成若干个链(链的根节点可以连向其他的点),然后将链首尾相连就可以得到环了。这样我们就可以只考虑一棵基环树,最后将答案相加。
我们看一个例子吧:
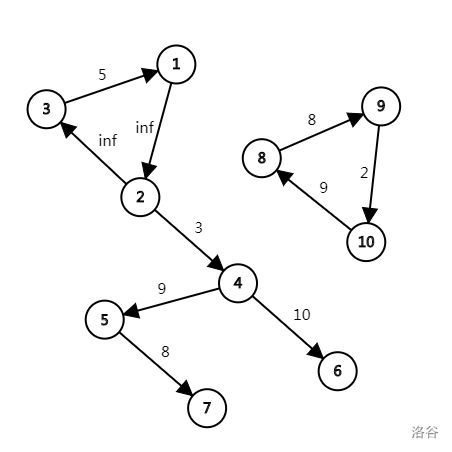
最优的做法是将 断开,得到 条链:
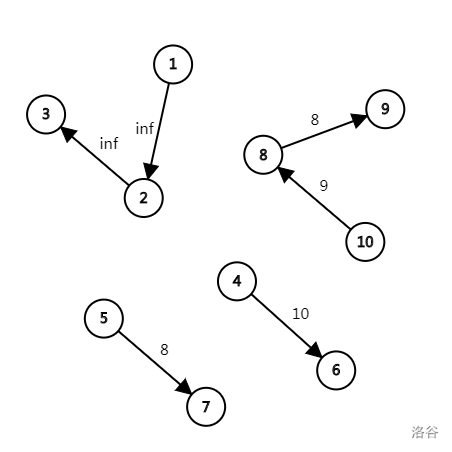
然后将 条链首尾相连,得到答案:
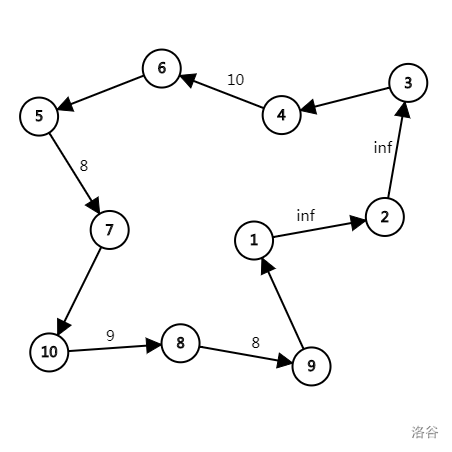
然后我们考虑每一棵基环树,因为每棵树只有一条入边,在环上的点都已经有了一条入边,只能向外连出边,因此这棵基环树显然是外向树。
对于每一棵根结点在环上的树,为了将其变为链,我们最多可以保留一个儿子,让它自己及其保留的儿子,保留的儿子保留的儿子……让这些点形成一条链。我们可以用贪心的思想,对于每个点我们保留它出边中费用最大的边,其他的边全部断掉,这样的话费一定是最小的。
(如在例子中断掉的 )
这样就可以写出处理树部分的代码了:
void dfs(long long x,long long last){ if(vis[x]==0) vis[x]=1; for(long long i=start[x];i;i=then[i]){ long long y=to[i]; if(y==last||vis[y]==2) continue; dfs(y,x); if(worth[out[x]]>worth[i]) ans+=worth[i]; else ans+=worth[out[x]],out[x]=i; } }经过这样的处理,我们就只剩一个环及这个环上的点连出的一些链了。
我们先找一下当前基环树的环,这个部分代码是很容易写出来的( 代表 点访问过, 代表 点在环上):
void find(long long x){ top=0; while(vis[x]==0) vis[x]=1,x=f[x]; while(vis[x]==1) stk[++top]=x,vis[x]=2,x=f[x]; }此时, 数组中存储的便是环上的点了。
考虑维护两个值:当前没有将整个环断成链的花费 与当前已经将整个环断成链的花费 。
我们思考一下,如何将当前剩下的点断成若干条链呢?发现环断开后只能带上一个点连出的链,而其他的链都必须断开。我们枚举每一个点,断开连入这个点的边,或者断开这个点带上的链,第一种操作会让之前的链保留下来(而上一个点带上的链可以与环上截下来的链成为新的链),第二种操作则可以维护现在链的形态。经过这样的操作,剩下的所有点都被分割为若干条链了。
我们注意一下:第一种操作会让一个没有断成链的环断成链(当然也可以让一个断成链的环断成更多的链),第二个操作则不会改变环的形态。因此 可以从两种操作转移(第一种操作可以从 与 转移来,而第二种操作只能从 转移来),而 只能从第二种操作转移(且由 转移过来)。
还是举个例子吧:
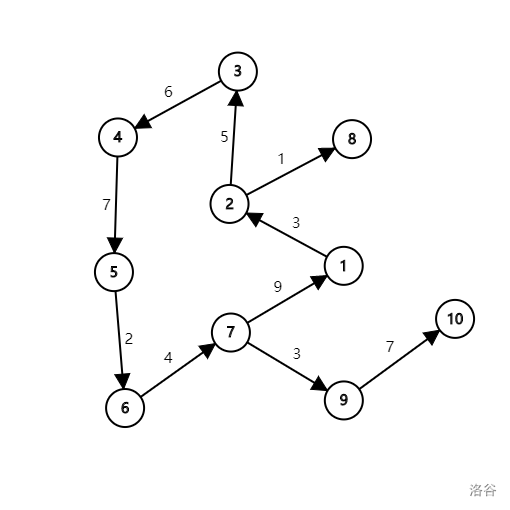
这个例子的答案应该是割掉 , 和 ,为 (感谢@M_theory004 的纠正),
至于为什么,读者自证不难。最后把答案累加就可以了。
这一部分的代码:
long long cut0=0,cut1=inf; for(j=1;j<=top;j++) dfs(stk[j],0); for(j=1;j<=top;j++){ cut1=min(min(cut0,cut1)+worth[in[stk[j]]],cut1+worth[out[f[stk[j]]]]); cut0+=worth[out[f[stk[j]]]]; } ans+=cut1;由于在函数与函数中每个点都只会遍历一遍,循环也只会将每个环及里面的点遍历一遍,因此复杂度是的。
代码
注: 与 分别指连向 的边编号与 连出的边的编号。
#include<stdio.h> #define inf 1000000000000000000 const int maxn=100005,maxm=200005; long long i,j,k,m,n,e,ans,top; long long start[maxn],to[maxm],then[maxm],worth[maxm],f[maxn],in[maxn],out[maxn],vis[maxn],stk[maxn]; inline long long min(long long a,long long b){ return a<b? a:b; } inline void add(long long x,long long y,long long z){ then[++e]=start[x],start[x]=e,to[e]=y,worth[e]=z; } void find(long long x){ top=0; while(vis[x]==0) vis[x]=1,x=f[x]; while(vis[x]==1) stk[++top]=x,vis[x]=2,x=f[x]; } void dfs(long long x,long long last){ if(vis[x]==0) vis[x]=1; for(long long i=start[x];i;i=then[i]){ long long y=to[i]; if(y==last||vis[y]==2) continue; dfs(y,x); if(worth[out[x]]>worth[i]) ans+=worth[i]; else ans+=worth[out[x]],out[x]=i; } } int main(){ scanf("%lld",&n); for(i=1;i<=n;i++){ long long x; scanf("%lld%lld",&f[i],&x); in[i]=i,add(f[i],i,x); } for(i=1;i<=n;i++){ if(vis[i]) continue; find(i); if(top==n){ puts("0"); return 0; } long long cut0=0,cut1=inf; for(j=1;j<=top;j++) dfs(stk[j],0); for(j=1;j<=top;j++){ cut1=min(min(cut0,cut1)+worth[in[stk[j]]],cut1+worth[out[f[stk[j]]]]); cut0+=worth[out[f[stk[j]]]]; } ans+=cut1; } printf("%lld\n",ans); return 0; }
- 1
信息
- ID
- 2684
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
