自动搬运

查看原文

来自洛谷，原作者为

	tommymio Cruel world

搬运于2025-08-24 21:51:10，当前版本为作者最后更新于2020-10-09 09:14:31，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

很有意思又偏向套路的换根 $\text{DP}$，考察了选手的模型转化能力。

我们发现，蓝线只会像是这个样子：

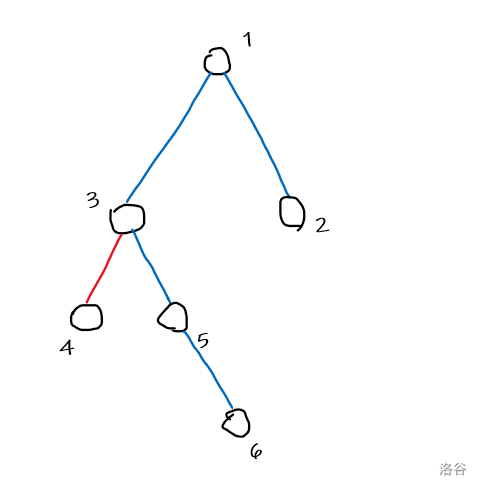
连接 $3,1,2$ 的蓝线是一类，连接 $3,5,6$ 的蓝线是另一类。由于无论哪类蓝线都只会连接三个点（理解一下），我们可以想到一个非常 $\text{Naive}$ 的树形 $\text{DP}$。设 $f_{x,{0/1}}$ 表示 $x$ 连接父亲的蓝边取或不取，按照题意转移即可。

但是这样是有问题的，有这种情况：

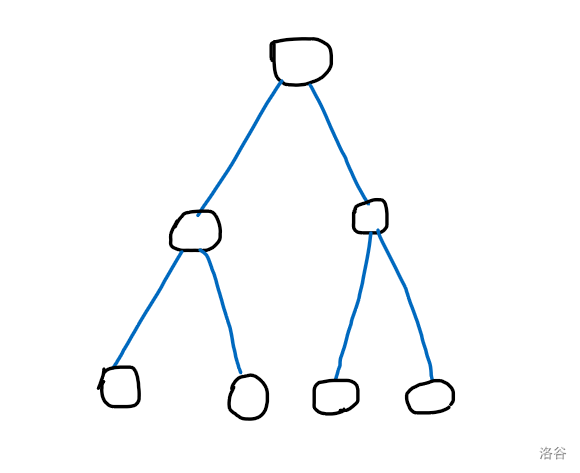
上述 $\text{DP}$ 会被这种数据 $\text{hack}$。因为无法判断两棵子树与他们共同的父亲之间是否能够连蓝边。

那么我们来考虑正确的做法。上述做法的正确性之所以不成立，是因为存在 $1,2,3$ 这种连边，我们能不能避免这种连边的出现呢？当然是可以的，我们发现，选择不同的根，只采用 $3,5,6$ 这种方式：父亲到儿子到孙子连蓝边，就能够覆盖所有的取兄弟和他们的父亲的连蓝边的方式，即 $3,1,2$ 这种方式。

这样就有了一个 $O(n^2)$ 的做法，枚举树的根，进行 $\text{DP}$。设 $f_{x,0}$ 为点 $x$ 不为蓝线中点，在 $x$ 的子树内的最大值。$f_{x,1}$ 为点 $x$ 为蓝线中点，在 $x$ 的子树内的最大值，有：

$$f_{x,0}=\sum_{y\in son_x}\max(f_{y,0},f_{y,1}+w(x,y)) $$$$f_{x,1}=f_{x,0}+\max_{y\in son_x}\{f_{y,0}+w(x,y)-max(f_{y,0},f_{y,1}+w(x,y))\} $$

对于每个根 $rt$，答案即为 $f_{rt,0}$，最后答案为在每个根 $rt$ 意义下的 所有 $f_{rt,0}$ 的最大值。

通过上述 $\text{DP}$ 式，我们能够得到一个固定根意义下的最大值，不妨选这个固定根为 $1$。现在考虑如何快速换根 $rt$ 得到 $rt$ 意义下的 $f_{rt,0}$。自然可以想到换根 $\text{DP}$。

现在重新对 $f$ 的概念强调，并定义新的量。$f_{x,0/1}$ 均为以 $1$ 为根意义下，$x$ 不在 $/$ 在蓝线中点，子树内的最大值。定义 $g_x$ 为以 $x$ 为根意义下，$f_{x,0}$ 的值。接下来要叙述 $k_{x,0/1}$ 的概念，配上一张图：

上图中被红色虚线圈出的部分就是 $k_{x,0/1}$ 包括的范围，按 $f_{x,0}$ 和 $f_{x,1}$ 的定义式转移。

最后列出 $g,k$ 的转移式：

$$g_{y,0}=f_{y,0}+\max(k_{x,0},k_{x,1}+w(x,y))$$ $$g_{y,1}=g_{y,0}+\max(\max_{i\in son_y}\{f_{i,0}+w(i,y)-\max(f_{i,0},f_{i,1}+w(i,y))\},k_{x,0}+w(x,y)-\max(k_{x,0},k_{x,1}+w(x,y)) $$$$k_{x,0}=g_{x,0}-\max(f_{y,0},f_{y,1}+w(x,y))$$ $$k_{x,1}=k_{x,0}+\max(\max_{i\in son_x\wedge i\neq y}\{f_{i,0}+w(i,x)-\max(f_{i,0},f_{i,1}+w(i,x))\},k_{fa,0}+w(x,fa)-\max(k_{fa,0},k_{fa,1}+w(x,fa))) $$

这个过程看上去似乎非常不自然，其实都是换根 $\text{DP}$ 的套路：考虑去掉即将要转移的 $y$ 后，对 $x$ 造成的影响及加上 $x$ 后，对 $y$ 造成的影响。

实现的时候，我们发现上述 $\text{DP}$ 式中有很多重叠的部分，换根时还有一些 $\max$ 的取值可能会取到 $y$ 相关的取值，维护一个相关的最大值和次大值即可。总时间复杂度为 $O(n)$，空间复杂度为 $O(n)$，比楼下奇奇怪怪的 $\text{vector}$ 跑得快/cy

如果看不懂上面的转移式可以看代码（逃

PS:此题 $\text{Luogu}$ 上数据过弱，建议上 $\text{UOJ}$ 上提交本题以确认算法正确性（

Show the Code

#include<cstdio>
#include<climits>
typedef long long ll;
int cnt=0;
ll mx1[200005],mx2[200005],vg[200005];
ll f[200005][2],g[200005][2],k[200005][2];
int son1[200005],son2[200005];
int h[200005],to[400005],ver[400005],w[400005];
inline int read() {
	register int x=0,f=1;register char s=getchar();
	while(s>'9'||s<'0') {if(s=='-') f=-1;s=getchar();}
	while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
	return x*f;
}
inline void add(int x,int y,int z) {
	to[++cnt]=y;
	ver[cnt]=h[x];
	w[cnt]=z;
	h[x]=cnt;
}
inline void swap(int &x,int &y) {int tmp=x;x=y;y=tmp;}
inline void swap(ll &x,ll &y) {ll tmp=x;x=y;y=tmp;}
inline ll max(const ll &x,const ll &y) {return x>y? x:y;}
inline void dfs1(int x,int fa) {
	mx1[x]=mx2[x]=INT_MIN; son1[x]=son2[x]=0;
	for(register int i=h[x];i;i=ver[i]) {
		int y=to[i];
		if(y==fa) continue;
		vg[y]=w[i];dfs1(y,x);
		f[x][0]+=max(f[y][0],f[y][1]+w[i]);
		ll val=f[y][0]+w[i]-max(f[y][0],f[y][1]+w[i]);
		if(mx1[x]<val) {son2[x]=son1[x];mx2[x]=mx1[x];son1[x]=y;mx1[x]=val;}
		else if(mx2[x]<val) {son2[x]=y;mx2[x]=val;}	
	}
	f[x][1]=f[x][0]+mx1[x];
}
inline void dfs2(int x,int fa) {
	for(register int i=h[x];i;i=ver[i]) {
		int y=to[i];
		if(y==fa) continue;
		if(son1[x]==y) {swap(mx1[x],mx2[x]);swap(son1[x],son2[x]);}
		k[x][0]=g[x][0]-max(f[y][0],f[y][1]+w[i]);k[x][1]=k[x][0]+mx1[x];
		if(fa!=-1) {k[x][1]=max(k[x][1],k[x][0]+k[fa][0]+vg[x]-max(k[fa][0],k[fa][1]+vg[x]));}
		g[y][0]=f[y][0]+max(k[x][0],k[x][1]+w[i]);
		if(mx1[x]<mx2[x]) {swap(mx1[x],mx2[x]);swap(son1[x],son2[x]);}
		dfs2(y,x);
	}
}
int main() {
	int n=read(); ll ans=0;
	for(register int i=1;i<n;++i) {int x=read(),y=read(),z=read(); add(x,y,z);add(y,x,z);}
	dfs1(1,-1); g[1][0]=f[1][0]; dfs2(1,-1);
	for(register int i=1;i<=n;++i) ans=max(ans,g[i][0]);
	printf("%lld",ans);
	return 0;
}