自动搬运

查看原文

来自洛谷，原作者为

	xgzc 苔花如米小，也学牡丹开。

搬运于2025-08-24 21:51:06，当前版本为作者最后更新于2019-03-31 15:10:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

神仙题目啊QwQ

设$f_i(x)$表示以第$i$个点为根的子树需要$x$秒引爆的代价。

我们发现，这个函数是一个下凸的一次分段函数。

考虑这个函数合并到父亲节点时会发生怎样的变化。

设$f_i'(x)$是原函数，$f_i(x)$是新函数，$i$和父亲之间的边长度为$l$，$[L, R]$是$f_i'(x)$斜率为$0$的那一段的左右端点的横坐标，那么有：

$$f_i(x) = \begin{cases}f_i'(x) + l & x \leq L \\f_i'(L) + (l - (x - L)) & L < x \leq L + l \\f_i'(L) & L + l < x \leq R + l \\f_i'(L) + ((x - R) - l) & R + l < x\end{cases} $$

我们一个一个来看。

首先第一个，当$x \leq L$时，我们肯定要让新的$l$越小越好，因为改变$l$的代价为$1$，而这个函数在$\leq L$的时候斜率$\leq -1$，即修改一次$x$的代价$\geq 1$，所以干脆将$l$变成$0$。

第二个，我们只要保证$x = L$就能取到函数的最小值，于是$l$的变化量越小越好。

第三个，我们不用改变$l$就可以保证能取到最小值，那就不用改变了。

第四个和第一个很像，这里就略去了。

---

那么这个过程究竟对这个函数做了什么改变呢？

我们将$\leq L$部分的函数向上平移了$l$单位，将$[L,R]$部分向右平移$l$单位，在$[L,L+l]$部分插入了一条斜率为$-1$的直线，并将$> R + l$的部分的斜率改为了$1$。

于是大概变成了这个样子（图源网络）：

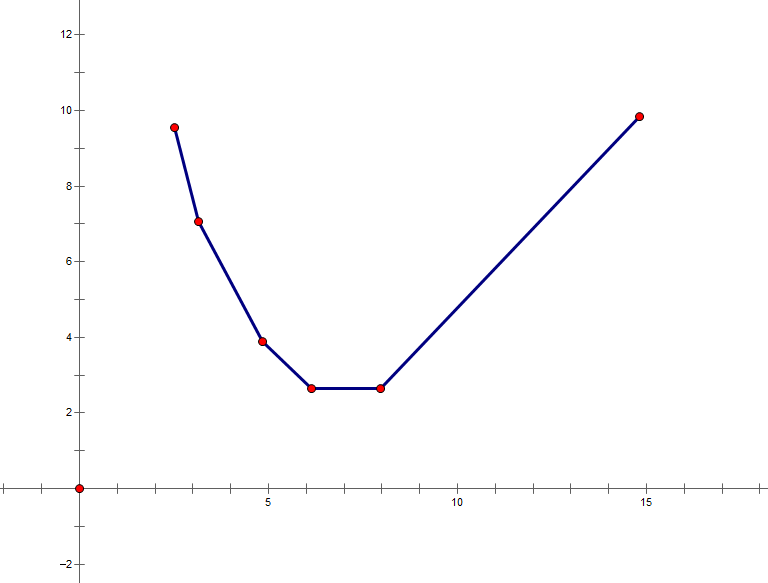
这样，各个拐点之间的直线的斜率是从左到右递增的。

我们不妨假设各个拐点之间的直线斜率的增量为$1$，如果有一个斜率不存在，那么我们就用两个同一位置的拐点来表示这个不存在的斜率。

然后我们发现我们只可能存下拐点的横坐标，于是怎么求函数值是一个问题。

我们如果能知道$f(0)$的值，这个事情就好办了。

$f(0)$的值还不好求？？？就是所有边权之和啊。

于是我们得到了通过拐点横坐标求得$f(L)$的方法，皆大欢喜。

那么我们知道每个函数被合并上去之前会变成什么样子了，那么我们也可以非常简单的合并两个函数了，我们只需要将两个函数的拐点列表合并一下就可以了。

我们再看看在合并到父亲节点时要做的操作：

一、将斜率$> 0$的那一段的斜率改为$1$。

因为我们合并上来的函数的斜率最大值都为$1$，所以我们只需要删除$k - 1$个最大的拐点即可，其中$k$是这个点儿子的数量。

二、将斜率$=0$的那一段平移$l$单位。

首先，我们做完一操作之后，横坐标最大的两个拐点就是斜率为$0$的两个端点了，将它们弹出来，加上$l$再放进去就没了。

三、加入一段斜率为$-1$的直线。

这个其实在做操作二的时候就顺带做完了。

我们维护一个可并堆就可以做上面的所有操作。

最后求答案时，我们保留$L$及其左边的拐点，依次减去它们的横坐标就是我们想要的函数值了。

代码见我的$\texttt{blog}$