自动搬运

查看原文

来自洛谷，原作者为

	Eleveslaine AFO

搬运于2025-08-24 21:51:00，当前版本为作者最后更新于2023-01-21 13:43:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

调了三天终于过了。
一道基于图论、初中平面几何基础的大模拟。
感谢

/www.desmos.com/calculator/emcwegdahq?lang=zh-CN)，其中所有点都可以拖动。绿点为浮标，数长度用。
彩蛋：不可以“不可以，总司令”。

题意

平面内给定起点 $S$、终点 $E$ 和 $n$ 个矩形。

• 走上下左右，只能在矩形边上转向，在平面的其他位置不能转向。
• 不能进入矩形内部。
• 可以以任意方向从起点出发。

求起点到终点的最短路径长度，或报告无解。

例如，本题样例中第一组数据如图所示。

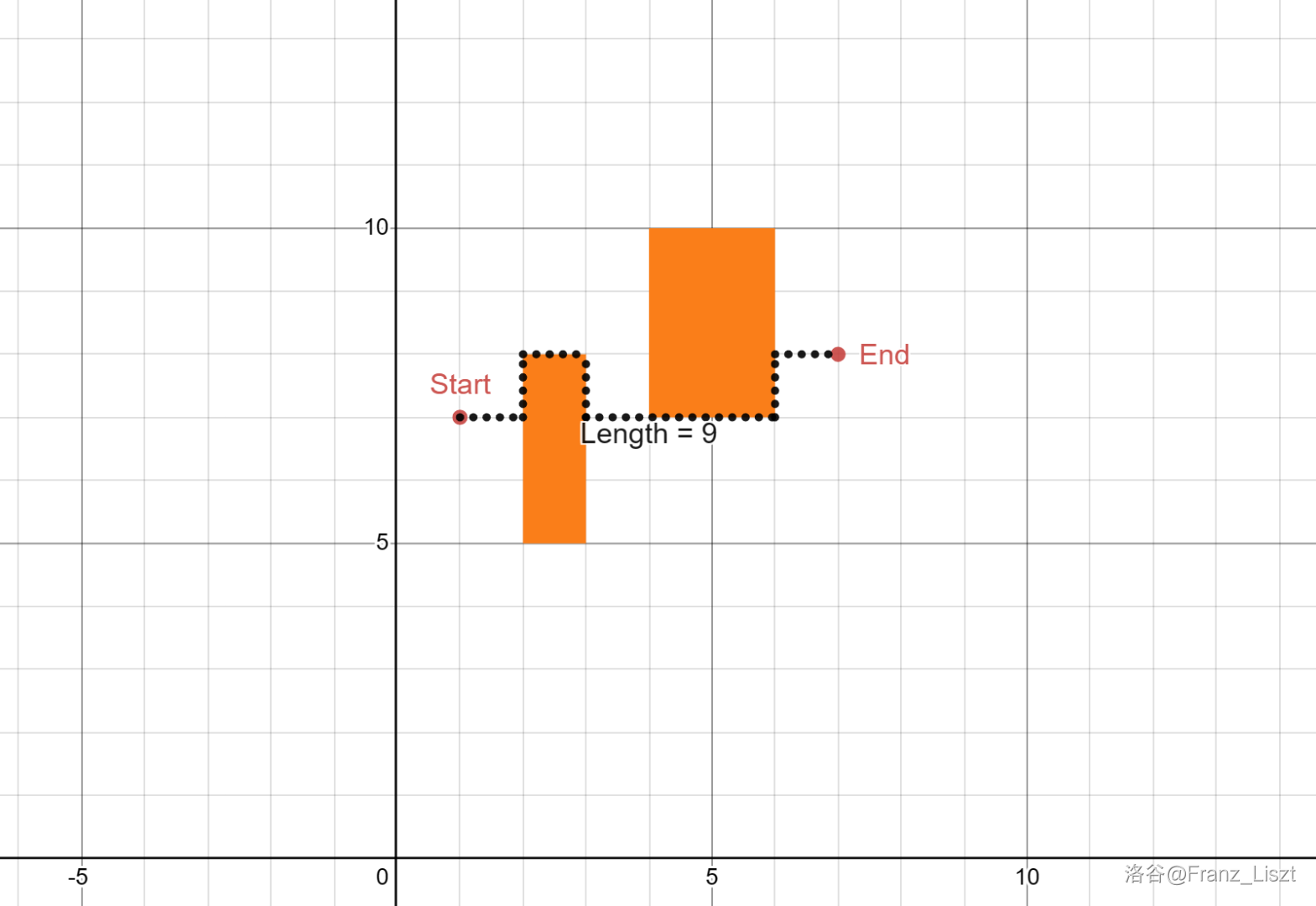
思路

对于此题，单纯的 BFS 难以实现，并且在时间复杂度上也无法接受，考虑连点、建图跑最短路。

准备工作

先写图论部分，实现链式前向星存图、加边和一种单源最短路算法即可。本题无负权，可以采用还没死的 Dijkstra 算法。代码实现上把所有图论内容放在 namespace Graph 中。
为了后续建图的方便，我们令本题中所有的长方形都长这个样子：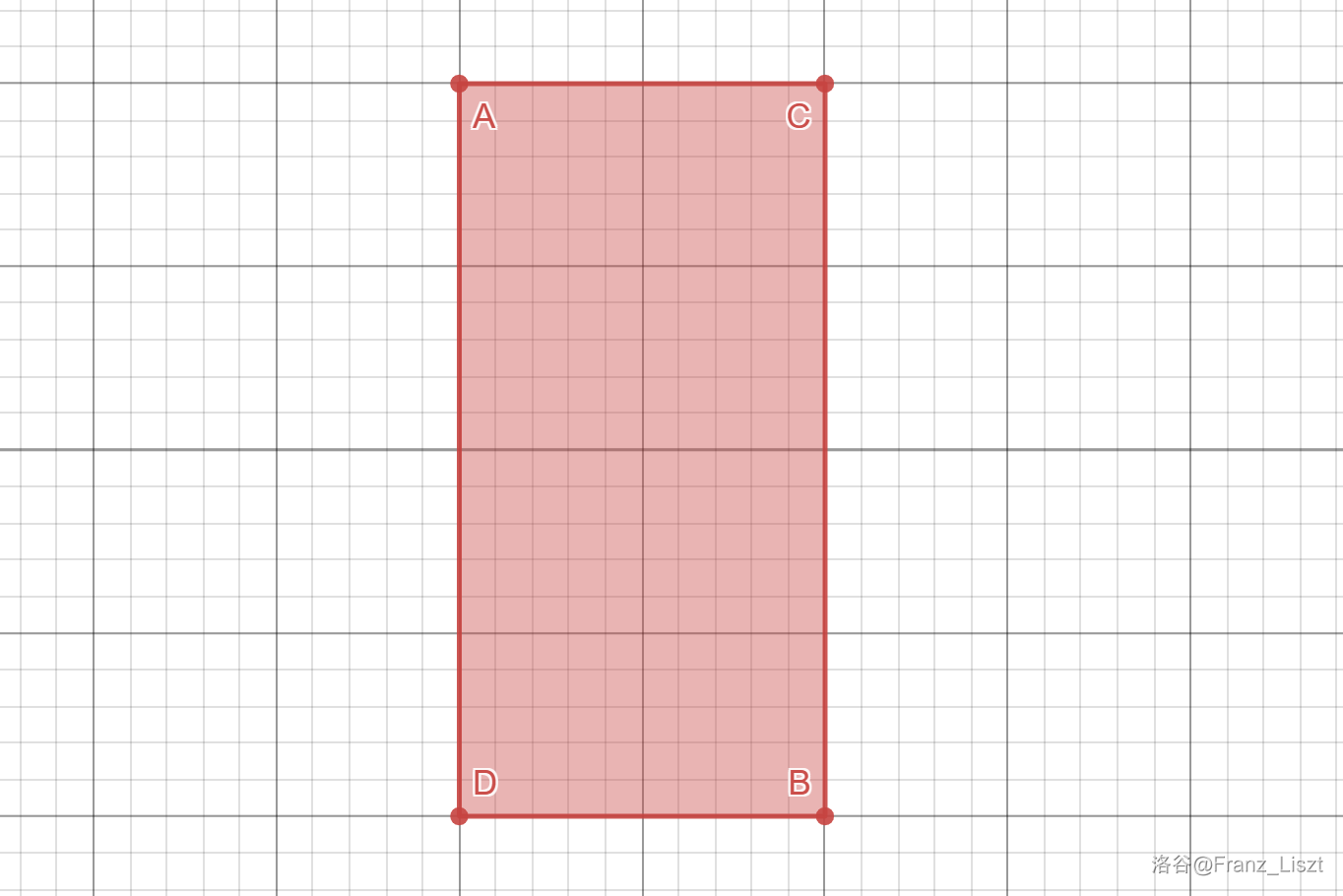

其中 $A,B$ 为输入的两点，保证 $x_A<x_B,y_A>y_B$。这样 $C,D$ 可以由 $A,B$ 的坐标得到，即 $C(x_B,y_A),D(x_A,y_B)$。为了保证 $A,B$ 相对位置正确，输入时需要视情况交换 $A,B$ 的某个坐标。

之后，需要进行离散化，实现几何点 $(x,y)\to$ 图中结点 $u$ 的映射。以下代码中，一些函数和自定义类可以看名称理解其作用。

// Point 为自定义类，有 int x,y 两个值
// 离散化，id[A] 表示 (A.x, A.y) 在图中结点编号
int cnt=0;
map <Point,int> id;
// 返回 (A.x, A.y) 在图中结点编号，没有的建立新点
inline int PointID(const Point &A)
{
    if(id[A]!=0)
        return id[A];
    ++cnt;
    return id[A]=cnt;
}
// 两点是否连接过
map <pair<Point,Point>,bool> connected;
// 在几何图形中连接两点，边权为其几何距离
inline void Connect(const Point &A,const Point &B)
{
    if(A==B||connected[(pair<Point,Point>){A,B}]||connected[(pair<Point,Point>){B,A}])
        return;
    connected[(pair<Point,Point>){A,B}]=connected[(pair<Point,Point>){B,A}]=1;
    // Dist(A,B) 为 A,B 之间的距离
    Graph::AddEdge(PointID(A),PointID(B),Dist(A,B));
    Graph::AddEdge(PointID(B),PointID(A),Dist(A,B));
}

连边建图

假设有一点 $P(x_P,y_P)$，需要实现一个函数 $\mathbf{Make}(P)$ 建立点 $P$ 与给出的 $n$ 个矩形可能的连边。
因为不能进入矩形内部，所以只要找到 $P$ 分别向上、向下、向左、向右距离最小的 $4$ 个矩形并连接即可。找最小值时遍历所有矩形，时间复杂度 $O(n)$，可以接受。
为了处理同一矩形的同一条边上出现两个不同点 $T_1,T_2$ 却没有在图中连接 $T_1T_2$ 的情况，定义矩形 $\alpha$ 的边 $m$ 上连接过的点集为 $\mathrm{coord[\alpha]}[m]$。例如，一个矩形 $\alpha$ 的边 $BD$ 形如 $D\text-T_1\text-\text-T_2\text-B$，则 $\mathrm{coord[\alpha]}[BD]=\{D,T_1,T_2,B\}$，最后再依次连接 $DT_1,T_1T_2,T_2B$。代码中使用默认有序的 STL set 实现，省去排序过程。
下面给出的伪代码描述了找点 $P$ 向上、向下 $2$ 个矩形并连接的过程，其中 $\mathrm{Rectangles}$ 为输入的矩形集，$\square ACBD$ 定义为线段 $AC,CB,BD,AD$ 上点的并集，$A_{\alpha},B_{\alpha}$ 等定义为矩形 $\alpha$ 的对应顶点。
找到交点后将交点放进所在矩形边的 $\text{coord}$ 集合中，最后再枚举矩形的每条边依次连接即可。

$$\begin{aligned} \ & \underline{\mathbf{Make}(P)}\\ 1\ & \mathrm{min}x_1,\mathrm{min}x_2 \gets +\infty; \alpha_1,\alpha_2 \gets \emptyset\\ 2\ & \mathbf{for}\ \square ACBD \in \mathrm{Rectangles}:\\ 3\ & \quad \mathbf{if}\ l:x=x_P \cap \square ACBD \ne \emptyset:\\ 4\ & \qquad \mathbf{if}\ P\ \mathrm{is\ below}\ \square ACBD:\\ 5\ & \qquad\quad \mathrm{Point}\ T=(l:x=x_P \cap BD)\\ 6\ & \qquad\quad\mathbf{if}\ |PT| < \mathrm{min}x_1:\\ 7\ & \qquad\qquad \mathrm{min}x_1 \gets |PT|\\ 8\ & \qquad\qquad \alpha_1 \gets \square ACBD\\ 9\ & \qquad \mathbf{else\ if}\ P\ \mathrm{is\ above}\ \square ACBD:\\ 10\ & \qquad\quad \mathrm{Point}\ T=(l:x=x_P \cap AC)\\ 11\ & \qquad\quad\mathbf{if}\ |PT| < \mathrm{min}x_2:\\ 12\ & \qquad\qquad \mathrm{min}x_2 \gets |PT|\\ 13\ & \qquad\qquad \alpha_2 \gets \square ACBD\\ 14\ & \mathrm{Point}\ T_1=(l:x=x_P \cap B_{\alpha_1}D_{\alpha_1})\\ 15\ & \mathrm{Point}\ T_2=(l:x=x_P \cap A_{\alpha_2}C_{\alpha_2})\\ 16\ & \mathrm{Connect}\ PT_1,PT_2 \\ 17\ & \mathrm{Insert}\ T_1\ \mathrm{to\ coord[\alpha_1]}[BD] \\ 18\ & \mathrm{Insert}\ T_2\ \mathrm{to\ coord[\alpha_2]}[AC] \\ \end{aligned} $$

求交点坐标可以使用初中平面几何相关知识。对向左、向右两个方向上矩形的处理与上面相似，不再展示。

实现 $\mathbf{Make}(P)$ 函数后，对每个矩形 $ACBD$ 依次对其四个顶点进行 $\mathbf{Make}$ 操作。另外别忘了对 $S,E\ \mathbf{Make}$ 一下。

特殊情况

1. $n=0$，即没有矩形。
   这时可以节省时间，如果 $S,E$ 同在一条平行于坐标轴的直线上，那么答案就是 $|SE|$；否则无解。

2. $S=E$，即起点终点重合。
   为了减少可能的麻烦这里特判一下，显然答案为 $0$。

3. $n \ne 0,S \ne E$ 且 $S,E$ 在同一条平行于坐标轴的直线上。
   如果没有考虑这种情况或处理不当会 WA on #6。此时若 $S,E$ 之间没有矩形需要连接 $SE$。这个判断直接枚举即可，时间复杂度为 $O(n)$，为减小常数与最后处理 $\mathrm{coord}$ 的循环合并。
   另外，有一篇题解直接连接了 $SE$ 而不考虑它们之间是否有矩形，针对此有 hack 数据，具体见此贴。

最后建完图以 $S$ 为起点跑一波 Dijkstra，如果结果为 inf，报告无解；否则输出最短距离。

代码

上面思路中提到的问题仅仅是对平面几何关系最简洁直观的描述。真正的实现需要判断点坐标之间的关系，略为复杂，但是都在初中平面几何知识范围内，推出来也并不难。
完整代码见云剪贴板。总时间复杂度 $O(n^2)$，并且已经尽量合并循环、减小常数，对本题的 $3\text s$ 时限绰绰有余。
另外多测记得清空，建图要清彻底，就因为这个调了三天才过。

最后求过一下吧（可怜）。另外以现在的标准，这题现在还没有合规的题解。