自动搬运

查看原文

来自洛谷，原作者为

	llzzxx712 屑大三

搬运于2025-08-24 21:50:58，当前版本为作者最后更新于2020-07-28 15:21:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P3629

解释详细，题目思路和所有涉及到的算法都有讲解。

代码精简清晰，不用STL，无压行代码59行。(核心代码只有：两次 dfs 共10行，标记直径 2行，dp 10行）

核心算法

两次dfs求树的直径 + 树上DP求树的直径 + 数学思考

题目分析

首先分析题目，刚开始这是一颗树，所以警车要将整个树遍历一遍再回到起点，边都为1,走的路程是 $2*(n-1)$ 。

所以我们只要算出修建新的道路可以让警车少走的边数，减一下就是答案了。

题目中的 K 只能是 1 或 2 ，所以我们先来看 k=1 的情况。

修了一条道路后，这棵树中就出现了一个环（也就是基环树，不知道也没关系），反正现在它有一个环，而因为我们只能经过新修的道路一次（0 和 2 都不行），所以我们肯定要将这个环走一遍。假设这个环中除去新加的边长度为 L ，那么我们少走的长度就是 L （原来要走两遍，现在只要一遍）。再加上新的边，因此要走的路就是 $2*(n-1)-L+1$ ，显然当 L 最大时这就是答案。一颗树中最长的一条路径就是它的直径，所以我们现在只要求出它的直径就可以了。

这里我们使用两次dfs求树的直径（原因下面会讲），因为这样可以知道直径的端点，进而确定整个直径的路线。

知道dfs求树的直径的可以跳过这一部分

树的直径有一个性质：距离树上一个点最远的点必定是直径的端点（之一）。

证明：反证法。假设 $a,b$ 是直径的两个端点，对于一个节点 $i$ ， 假如节点 $c$ 距离 $i$ 比$a,b$ 距离 $i$ 都要远，那么 $c$ 一定可以和 $a,b$ 中的一个节点构成一条更长的路径，与假设不符。性质成立。

这样，我们通过一次 dfs 比较深度，求出了直径的一个端点，那么接下来再以端点为根来一次 dfs ，标记路径并记录长度。

两次dfs代码基本一样，除了第二次要处理 $fa$ 数组。$fa$ 数组用来存每个节点的父亲。

#define N 100010
int head[N],ne[N<<1],to[N<<1],size[N<<1];//邻接表存边,size[ ] 存边权，一开始都是 1
int fa[N],de[N];//de[ ] 存深度

void dfs(int x,int pre,int z,int t){//x表示当前节点，pre 是它的父亲，z的边权，t表示第几次 dfs 。
	de[x]=de[pre]+z;
	if(t==2) fa[x]=pre;//第二次跑dfs记录直径 
	for(int i=head[x];i;i=ne[i]){
		int y=to[i],z=size[i];
		if(y==pre) continue;
		dfs(y,x,z,t);
	}
	if(de[x]>de[leaf]) leaf=x;//leaf 存直径的端点，易知它一定是叶节点
}

此时 k=1 的情况就解决了，你可以拿到 30分 。

建立第二条道路后，又会形成一个环。若两个环不重叠，我们只要像刚才那样处理就好了。但如果重叠呢？按照题目的要求，新边必须被走仅一次，所以重叠的边必须走两遍。

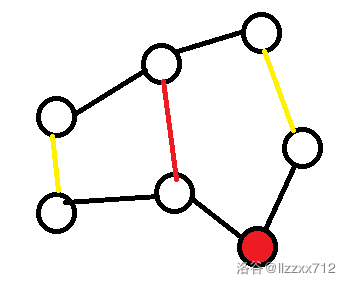
如图，我们从红色点开始走，黄色边为新修建的边，红色边为重叠边，易知红边要走两次。 所以在计算答案的时候我们需要将重叠边减去或是不选重叠边，因此我们可以将第一次求的直径取反这样如果选到了原直径上的边就相当于减去了这部分,保证了答案正确。这也就是我们刚才需要用dfs求直径的原因。

将边权取反后新的树上再求直径，设长度为 L2，那么答案就是 $2*(n-1)-(L1-1)-(L2-1)=2*n-L1-L2$

如何标记刚才求出的直径呢？ 我们只要从刚才求出的 leaf （端点）开始往上标记直径中的节点就好了。

for(int i=leaf;i;i=fa[i]) v[i]=1;

如果碰到两个点都被标记的情况，就将这条边边权取反。

因为dfs不能处理负边权情况，所以第二次求直径需要用 DP 。知道DP求树的直径的同志就可以结束这篇题解了（能给个赞就更好了）。

我们先随便找一个点（比如1号点），把这个无根树当成有根树， $d[x]$ 表示从 x 出发走向以 x 为根的子树可以走到的最远距离，显然叶子节点 $i$ 的 $d[i] = 0$ ，它父亲节点 $j$ 的 $d[j]=max(d[j],d[i]+edge_{i,j})$ 我们可以递归地求出每一个点的 $d$ 。然后一条路径的长度就是两个点的 $d$ 之和加上他们直径的距离，也就是 $d[x]+d[y]+edge_{x,y}$ ，当我们递归地处理时，假如 x 是父节点，处理到 y 时肯定已经将前面的几个节点处理过了，所以可以直径更新$ans$ 。也就是 $ans=max(ans,d[x]+d[y]+size[i])$ （我用 size 存边权）

DP完整代码：

void dp(int x,int pre){//pre 是父亲 
	for(int i=head[x];i;i=ne[i]){
		int y=to[i];
		if(y==pre) continue;//无根树 
		if(v[x]&&v[y]) size[i]=-1;//两点有标记，边权变负 
		dp(y,x);//递归处理 
		L2=max(L2,d[x]+d[y]+size[i]);//更新答案 
		d[x]=max(d[x],d[y]+size[i]);
	} 
}

完整AC代码

#include<bits/stdc++.h>
using namespace std;
void read(int &x){
	int f=1;x=0;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();}
	x*=f;
}
#define N 100010
int n,k,tot,leaf=1,leaf1=1,L1,L2; 
int head[N],ne[N<<1],to[N<<1],size[N<<1];
int fa[N],de[N];
int v[N],d[N];
void add(int x,int y,int z){
	to[++tot]=y;
	ne[tot]=head[x];
	size[tot]=z;
	head[x]=tot;
}
void dfs(int x,int pre,int z,int t){//x表示当前节点，pre 是它的父亲，z的边权，t表示第几次 dfs 。
	de[x]=de[pre]+z;
	if(t==2) fa[x]=pre;//第二次跑dfs记录直径 
	for(int i=head[x];i;i=ne[i]){
		int y=to[i],z=size[i];
		if(y==pre) continue;
		dfs(y,x,z,t);
	}
	if(de[x]>de[leaf]) leaf=x;//leaf 存直径的端点，易知它一定是叶节点
}
void dp(int x,int pre){//pre 是父亲 
	for(int i=head[x];i;i=ne[i]){
		int y=to[i];
		if(y==pre) continue;//无根树 
		if(v[x]&&v[y]) size[i]=-1;//两点有标记，边权变负 
		dp(y,x);//递归处理 
		L2=max(L2,d[x]+d[y]+size[i]);//更新答案 
		d[x]=max(d[x],d[y]+size[i]);
	} 
}
int main(){
	read(n),read(k);
	for(int i=1;i<n;i++){
		int x,y;
		read(x),read(y);
		add(x,y,1),add(y,x,1);
	}
	dfs(1,0,0,1);
	dfs(leaf,0,0,2);
	L1=de[leaf];
	if(k==1){
		printf("%d",2*(n-1)-L1+1);
		return 0;
	}
	for(int i=leaf;i;i=fa[i]) v[i]=1;
	dp(1,0);
	cout<<n*2-L1-L2;	
	return 0;
}

有什么不理解的地方或建议可以评论或私信我，如果题解对你有帮助，给个赞呗。