自动搬运

查看原文

来自洛谷，原作者为

	Lucaster_ Do not go gentle into that lonely night

搬运于2025-08-24 21:50:56，当前版本为作者最后更新于2019-06-06 20:35:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

这次改一下题解风格，先不放AC代码 （因为实在是太长了）

（哦对了）

先放上程序“缩略图”：

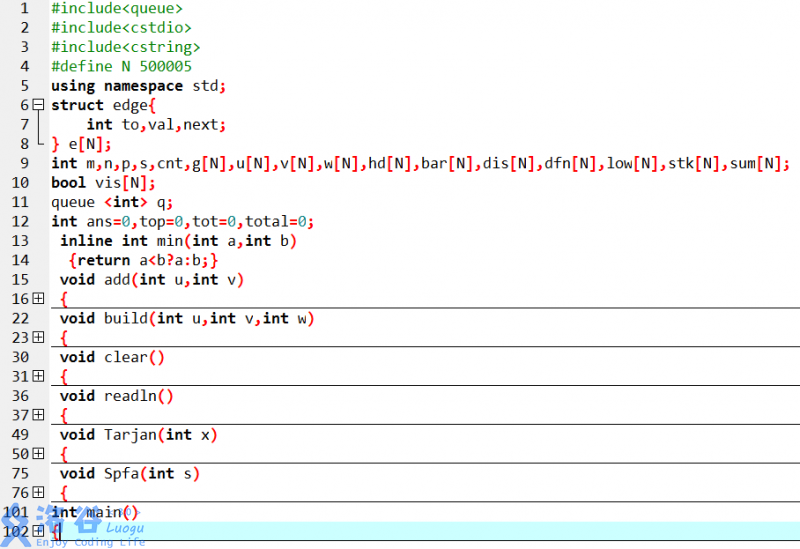
你看这个数组个数，你看这个过程（void）个数， （你看这个好看的马蜂） 是不是有点头大

不急，我们就按照我代码中一部分一部分来讲——

前置芝士：

1. 邻接表存储/遍历（如果你这个都不会的话做这种综合大题有点早……先好好学图论吧）
2. SPFA跑最长路（其实改个符号就好，没有必要建负权边跑最短路）
3. Tarjan缩点（不会的同学先学好Tarjan再来做这道题哦，Tarjan练习题）

OK，现在假设上面的东西你都会，那么正式开始讲解：

再补充一句：这道题确实是道好题，我的题解会讲的很详细，如果你很想理解，做出这道题，最好耐心看完。如果没有耐心，吃亏的可不是我。

1.邻接表存储

这里我们用两个过程来存，一个add（存无边权的图），一个build（有边权）

先放上代码，等会就知道为什么要用两个了

 void add(int u,int v)
 {
 	cnt++;
 	e[cnt].to=v;
 	e[cnt].next=hd[u];
 	hd[u]=cnt;
 }

 void build(int u,int v,int w)
 {
 	cnt++;
 	e[cnt].to=v;
 	e[cnt].val=w;
 	e[cnt].next=hd[u];
 	hd[u]=cnt;
 }

2.输入部分

这道题的输入数据还是比较麻烦的

首先用数组存一下每条边的起点终点

等等，为什么要用数组存呢，直接输入不行吗

自己先想一下，虽然我一开始也没想到

这倒跟建边没什么关系
我们这么做主要是为了后面服务的
因为后面我们要用Tarjan缩点，缩完点以后有可能你一开始输入的那组边“就是一个点了”
不用数组存一下的话无法进行后续操作了
如果不理解的话就先搁着，后头主函数和Tarjan中会详细讲解

然后再输入s，p

再输入每个酒吧，这个是为了最后遍历一遍dis[酒吧]所服务的。

当然你也可以在main中输入，省掉一个存酒吧位置的数组

等会详细说

代码就长这样：

 void readln()
 {
 	clear();
 	scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u[i],&v[i]);
        add(u[i],v[i]);
    }
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    scanf("%d%d",&s,&p);
    for(int i=1;i<=p;i++) scanf("%d",&bar[i]);
 }

u,v,w表示边起点，终点，点权的数组 bar是酒吧的英文，表示酒吧位置

眼尖的同学这时候要问了：clear是个什么东西

放心这次没 开挂 使用stl，这是我手写的一个清空数组的函数

长这样：

 void clear()
 {
 	cnt=0;
 	memset(e,0,sizeof(e));
 	memset(hd,0,sizeof(hd));
 }

对邻接表很熟悉的同学一看就懂：这是清空邻接表的操作啊（cnt归零，hd清零，边表也清零）

这里教大家一种memset的用法（我也是从楼下大佬中找的）

memset(结构体名字，值，sizeof(结构体名字))

这样可以直接清空（赋值）一个结构体哦

前提是你结构体中的类型要统一，比如说都是int

3.Tarjan缩点

void Tarjan(int x)
 {
 	dfn[x]=low[x]=++total;
 	stk[++top]=x;vis[x]=true;
 	for(int i=hd[x];i;i=e[i].next)
 	{
 		int t=e[i].to;
 		if(!dfn[t])
 		{
 			Tarjan(t);
 			low[x]=min(low[x],low[t]);
 		}
 		else if(vis[t])
 		 low[x]=min(low[x],dfn[t]);
 	}
 	if(dfn[x]==low[x])
 	{
 		tot++;
 		do{
 			int tp=stk[top];
 			sum[tot]+=w[tp];
 			vis[tp]=false;
 			g[tp]=tot;
 		}while(stk[top--]!=x);
 	}
 }

基本就是标准Tarjan，我讲下不一样的地方吧：

tot++;
do{
 int tp=stk[top];
 sum[tot]+=w[tp];
 vis[tp]=false;
 g[tp]=tot;
}while(stk[top--]!=x);

这里我是用的数组模拟栈，首先int tp=stk[top]取出栈顶

sum表示缩完点后这个点的点权
不是很懂Tarjan的好好理解下Tarjan弹栈的部分再看这里就懂了
懂Tarjan的模拟一下应该就懂了，每次弹栈时，所有被弹出的点都是缩完点后的一个点
即sum[tot]+=w[tp]，缩完点后的点权+=原点权
很好理解吧
不懂的说明你对Tarjan还是理解不到位……这篇题解不是讲Tarjan的，楼下大佬应该有详细讲解。

然后vis[tp]=false表示tp已经出栈

g表示缩完点后每个点在哪个点中
即g[tp]=tot，tp这个点在缩完点后的第tot个点里
然后用栈顶和x比较，标准Tarjan操作

stk[top--]就相当于pop弹栈了

大家应该都看懂了吧

那现在我们就已经缩好点了，g已经记录好了，sum也记录好每个新点的点权了

5.先来看下主函数

int main()
{
    readln();
    for(int i=1;i<=n;i++)
     if(!dfn[i]) Tarjan(i);
    clear();
    for(int i=1;i<=m;i++)
     if(g[u[i]]!=g[v[i]])
      build(g[u[i]],g[v[i]],sum[g[v[i]]]);
    Spfa(s);
    for(int i=1;i<=p;i++)
     ans=max(ans,dis[g[bar[i]]]);
    printf("%d",ans);
    return 0;
}

首先readln输入，就是第二部分（P党转来的我喜欢用readln嘿嘿）

然后标准Tarjan，if(!dfn[i]) Tarjan(i);

---(这里也是听别的大佬说的，Tarjan首字母最好大写，避免一些神奇的错误)

这时候clear就有用了，因为我们之前add建的图是为了Tarjan缩点用的，现在缩好点了那张图就没用了！我们没有必要新开一个结构体，反而浪费很多内存，把刚刚的图clear一下就好了

然后我们遍历每一条输入的边，这个时候之前的u,v数组就有用了！我们通过判断u[i],v[i]是否在一个新点里，如果不在的话就build一条新边，这样就能建一个缩完点后的图

注意build：起点是u[i]所在的缩点，终点是v[i]所在的缩点（如果u[i]和v[i]在一个缩点里就不会执行build了），边权是v[i]所在缩点的点权（sum）！！！

这样，这张新图就表明：从U走到V可以抢劫W的钱，钱数当然是缩点点权啊

没问题

吧？

有点问题的哦：相信不少同学也看出来了——那你这样每次把边权设置为后头那个缩点的点权，前头那个点被冷落了，点权不就没用了吗？

能想到这，恭喜你你理解这道题了

不过这个问题确实存在，我们的解决方案也很简单粗暴

直

接

来

看

6.Spfa跑最长路

正如一开始所说，我就是改了个符号，没有建负边权跑最短路，所以这一部分也是非常好理解的啦

直接上代码咯，spfa板子

 void Spfa(int s)
 {
 	for(int i=1;i<=tot;i++) dis[i]=0;
 	int gs=g[s];
    q.push(gs);
 	vis[gs]=true;
 	dis[gs]=sum[gs];
 	while(!q.empty())
 	{
 		int h=q.front();q.pop();
 		vis[h]=false;
 		for(int i=hd[h];i;i=e[i].next)
 		{
 			int t=e[i].to;
 			if(dis[t]<dis[h]+e[i].val)最短路中这里是>号，改成<号就是最长路咯
 			{
 				dis[t]=dis[h]+e[i].val;
 				if(!vis[t])
 				{
 					q.push(t);
 					vis[t]=true;
 				}
 			}
 		}
 	}
 }
 一看这个鬼畜的大括号就是spfa hhhhhhhh

我们来解决刚刚的问题，起点的点权怎么办

你会发现，spfa又不完全是板子，我改了几个地方：

int gs=g[s];
q.push(gs);
vis[gs]=true;
dis[gs]=sum[gs];

起点不是s了，而是g[s]，dis[起点]也不是0了

为什么呢？

你先想一下

——

——

——

想不出来？缩点是干啥用的来着？

——

——

——

想出来了吧：

我们刚刚build建的图是一张缩完点后的缩点图，所以我们push起点的时候当然是push缩完点后s所在的点啊

为什么呢？万一s本身就在一个环里，push（s)的话问题就大了

所以我们把起点一律改成g[s]来操作

并且，我们把起点的dis值直接加上点权，这样就不会漏掉起点点权了

而且放心，一开始更改dis值不会对后续松弛操作造成无法更改的影响，毕竟这是最长路

然后

然后

这道题就没什么可讲的了吧

最后再处理完主函数中这一部分：

for(int i=1;i<=p;i++)
 ans=max(ans,dis[g[bar[i]]]);
printf("%d",ans);
return 0;

最后还是放上完整AC代码吧：

#include<queue>
#include<cstdio>
#include<cstring>
#define N 500005
using namespace std;
struct edge{
    int to,val,next;
} e[N];
int m,n,p,s,cnt,g[N],u[N],v[N],w[N],hd[N],bar[N],dis[N],dfn[N],low[N],stk[N],sum[N];
bool vis[N];
queue <int> q;
int ans=0,top=0,tot=0,total=0;
 inline int min(int a,int b)
  {return a<b?a:b;}
 void add(int u,int v)
 {
 	cnt++;
 	e[cnt].to=v;
 	e[cnt].next=hd[u];
 	hd[u]=cnt;
 }
 void build(int u,int v,int w)
 {
 	cnt++;
 	e[cnt].to=v;
 	e[cnt].val=w;
 	e[cnt].next=hd[u];
 	hd[u]=cnt;
 }
 void clear()
 {
 	cnt=0;
 	memset(e,0,sizeof(e));
 	memset(hd,0,sizeof(hd));
 }
 void readln()
 {
 	clear();
 	scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u[i],&v[i]);
        add(u[i],v[i]);
    }
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    scanf("%d%d",&s,&p);
    for(int i=1;i<=p;i++) scanf("%d",&bar[i]);
 }
 void Tarjan(int x)
 {
 	dfn[x]=low[x]=++total;
 	stk[++top]=x;vis[x]=true;
 	for(int i=hd[x];i;i=e[i].next)
 	{
 		int t=e[i].to;
 		if(!dfn[t])
 		{
 			Tarjan(t);
 			low[x]=min(low[x],low[t]);
 		}
 		else if(vis[t])
 		 low[x]=min(low[x],dfn[t]);
 	}
 	if(dfn[x]==low[x])
 	{
 		tot++;
 		do{
 			int tp=stk[top];
 			sum[tot]+=w[tp];
 			vis[tp]=false;
 			g[tp]=tot;
 		}while(stk[top--]!=x);
 	}
 }
 void Spfa(int s)
 {
 	for(int i=1;i<=tot;i++) dis[i]=0;
 	int gs=g[s];
    q.push(gs);
 	vis[gs]=true;
 	dis[gs]=sum[gs];
 	while(!q.empty())
 	{
 		int h=q.front();q.pop();
 		vis[h]=false;
 		for(int i=hd[h];i;i=e[i].next)
 		{
 			int t=e[i].to;
 			if(dis[t]<dis[h]+e[i].val)
 			{
 				dis[t]=dis[h]+e[i].val;
 				if(!vis[t])
 				{
 					q.push(t);
 					vis[t]=true;
 				}
 			}
 		}
 	}
 }
int main()
{
    readln();
    for(int i=1;i<=n;i++)
     if(!dfn[i]) Tarjan(i);
    clear();
    for(int i=1;i<=m;i++)
     if(g[u[i]]!=g[v[i]])
      build(g[u[i]],g[v[i]],sum[g[v[i]]]);
    Spfa(s);
    for(int i=1;i<=p;i++)
     ans=max(ans,dis[g[bar[i]]]);
    printf("%d",ans);
    return 0;
}

完结撒花！