自动搬运

查看原文

来自洛谷，原作者为

	3493441984zz **

搬运于2025-08-24 21:50:51，当前版本为作者最后更新于2019-02-15 14:00:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题外话：

题解好像没有图，发个有图的，希望能帮助你们更好的理解

思路：

其实就是一个贪心吧，见的挺多的，一开始做的话很难想到这个反悔机制

转化问题

我们把每相邻两个办公楼之间的距离算出来，抽象出来点，也就是有$n-1$个点，第$i$个点的点权表示第$i$栋楼与第$i+1$栋楼的距离

那么，当我们选了第$i$个点时，我们就不能再选$i-1,i+1$这两个点了，为什么呢？因为选了第$i$个点的话，就不能再有电缆连接第$i$和第$i+1$栋楼了，而选$i-1,i+1$这两个点的话，又会连接一下第$i$或第$i+1$栋楼，不符合题意。

那么这样做了之后，题目就变为，给定$n-1$个点，要你选出$k$个点，并且这$k$个点两两不相邻（如果没看懂请重复看上面这段话）

那么问题转化了之后呢？？？

我们先来看一个错误的思路：

我们弄一个小根堆（本蒟蒻用的优先队列代替）

把每一个点放进去，然后每次贪心取最小值，取了一个点后就把相邻的点标记为不能取

如果你认为这是对的话，就看看下面这个样例（楼层$5$个，要连接电缆数$2$个）：

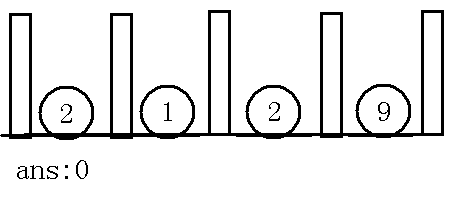
长方形是楼层，圆形是抽象出来的点，那么如果按照上面的思路的话，我们会先取$1$，也就是下图：

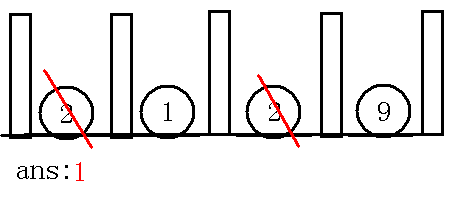
那么我们就只能取$9$了，答案就是$10$，可是，这是最优的吗？？

我们用肉眼都能看出来选择$2,2$更优,那么我们就要增添一个反悔机制：

当我们取了一个点后，我们要再加入一个点，这个点的权值为左边的点权$+$右边的点权$-$自身的点权,为什么这样就能反悔了呢？？

我们边模拟边解释：

当我们取了$1$点后，把两个$2$标记为访问过,并且更新$1$节点的左右，$1$节点左边已经空了，右边则是$9$节点，然后在$1$节点位置加入一个点权为$2+2-1$的点

如下图：

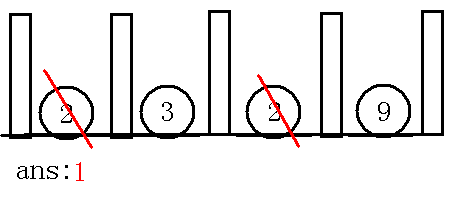
那么优先队列下一个点为$2$，而$2$被访问过了，直接下一个点，下一个点还是$2$，而$2$也被访问过了，再下一个点，下一个点为$3$，把与它相邻的$9$标记为访问过，而且现在已经取了$2$个点了（本样例题目规定了安装$2$条电缆）所以更新$ans$，并且退出

最后如下图：

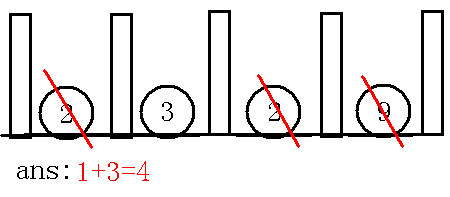
看出来了吗？其实这就相当于我们取了$2,2$两个点，为什么呢？$ans=1+3$,也等于$2+2$呀，还记得$3$怎么来的吗？$3=2+2-1$，那么代回去就是

$4=1+3=1+2+2-1=2+2$

也就是说取了$3$这个点，就相当于没有取$1$这个点，而是取了$2,2$这两个点

你看懂了这个反悔机制吗$qwq$

至于左右节点的更新，我们用双向链表实现：

接下来是美滋滋的代码时间~~~

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define N 500007
#define inf 0x3f3f3f3f
using namespace std;
struct Place
{
	int val,l,r;
}p[N];
struct Node
{
	int val,id;
	bool operator <(Node it) const
	{
		return val>it.val;
	} 
};
int n,m,ans,last;
bool vis[N];
priority_queue<Node> q;
void Del(int x)
{
	p[x].l=p[p[x].l].l;
	p[x].r=p[p[x].r].r;
	p[p[x].l].r=x;
	p[p[x].r].l=x;
}
int main()
{
	scanf("%d%d%d",&n,&m,&last);
	for(int i=1;i<n;++i)
	{
		int in;
		scanf("%d",&in);
		p[i].val=in-last;
		last=in;
		p[i].l=i-1;
		p[i].r=i+1;
		q.push((Node){p[i].val,i});
	}
	p[0].val=p[n].val=inf;//注意这里 
	for(int i=1;i<=m;++i)
	{
		while(vis[q.top().id])
			q.pop();
		Node now=q.top();
		q.pop();
		ans+=now.val;
		vis[p[now.id].l]=vis[p[now.id].r]=1;
		p[now.id].val=p[p[now.id].l].val+p[p[now.id].r].val-p[now.id].val;
		q.push((Node){p[now.id].val,now.id});
		Del(now.id);
	}
	printf("%d",ans);
	return 0;
}