自动搬运

查看原文

来自洛谷，原作者为

	disposrestfully **

搬运于2025-08-24 21:50:24，当前版本为作者最后更新于2019-07-01 17:59:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

对于$p\le2$的情况我们都能直接判断,考虑$p=3$.

一个比较显然的想法是把所有数字从小到大放到环上,记录之前放的三个数之间有没有空位,以及这三个数是否在环的端点上.

但这个做法非常麻烦,并且复杂度并不是很优秀.

官网上给出了一种更加巧妙的解法.

我们先把编号$i$变成$n-i$,那么我们现在要求的是以$0$开头,以$1/2/3$结尾的,满足题目里附加条件的数列的数量.

我们设$f[i]$表示以$i$开头$i+1$结尾,值域为$[i,n)$的,满足题目附加条件的数列的数量.

同时我们设$g[i]$表示以$i+1$开头$i$结尾,值域为$[i,n)$的,满足题目附加条件的数列的数量.

看上去似乎完全不能转移.

我们先考虑$n$较小的情况,这时候我们可以通过搜索求出$f$数组和$g$数组.具体的过程大概是先确定头尾,然后不断往中间插入数字知道填满整个数列为止.

这个过程可以记忆化,如果我们发现这个数列两端的数的差为$1$,那么我们可以在此停止搜索.

好的让我们来看看搜出的是什么东西.

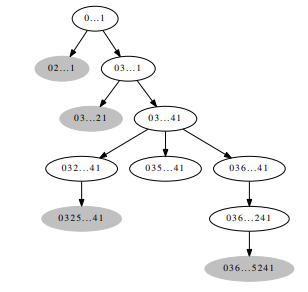
于是有$f[i]=g[i+1]+g[i+2]+g[i+4]+g[i+5]$

因为$f$和$g$的状态设计是对称的所以$g[i]=f[i+1]+f[i+2]+f[i+4]+f[i+5]$

要注意的是这个式子只在$i\le n-8$的时候成立,对于$i$更大的情况是需要真的去搜的.

现在我们需要分别统计以$1/2/3$结尾的数列的数量$Ans_1/Ans_2/Ans_3$,显然$Ans_1=f[0]$,至于$Ans_2$和$Ans_3$,我们手玩一下.

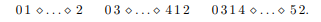
好的那么$Ans_2=f[1]+f[3]+f[4]$

$Ans_3=f[2]+f[4]+f[5]+g[3]+g[4]$

复杂度$O(n)$,代码难度不大.

#include<bits/stdc++.h>
#define read() Read<int>()
namespace pb_ds{   
    namespace io{
        const int MaxBuff=1<<15;
        const int Output=1<<23;
        char B[MaxBuff],*S=B,*T=B;
		#define getc() ((S==T)&&(T=(S=B)+fread(B,1,MaxBuff,stdin),S==T)?0:*S++)
        char Out[Output],*iter=Out;
        inline void flush(){
            fwrite(Out,1,iter-Out,stdout);
            iter=Out;
        }
    }
    template<class Type> inline Type Read(){
        using namespace io;
        register char ch;
        register Type ans=0; 
        register bool neg=0;
        while(ch=getc(),(ch<'0' || ch>'9') && ch!='-');
        ch=='-'?neg=1:ans=ch-'0';
        while(ch=getc(),'0'<= ch && ch<='9') ans=ans*10+ch-'0';
        return neg?-ans:ans;
    }
    template<class Type> inline void Print(register Type x,register char ch='\n'){
        using namespace io;
        if(!x) *iter++='0';
        else{
            if(x<0) *iter++='-',x=-x;
            static int s[100]; 
            register int t=0;
            while(x) s[++t]=x%10,x/=10;
            while(t) *iter++='0'+s[t--];
        }
        *iter++=ch;
    }
}
using namespace pb_ds;
using namespace std;
typedef long long ll;
const int N=1e6+5;
const int Mod=1e9+7;
inline void ad(int &x,int y){
	x+=y;
	if (x>=Mod) x-=Mod;
}
int n,m,k,ans;
int f[N],g[N];
bool a[N][7],vis[N];
#define chk(x,y) (!a[(x)][(y)-(x)+3])
namespace sub2{
	int tot,ans;
	int p[N];
	inline void work(){
		ans=2;
		for (int i=1;i<=n;++i){
			if (i&1) p[(i+1)>>1]=n-i;
			else p[n-(i>>1)+1]=n-i;
		}
		p[0]=p[n],p[n+1]=p[1];
		for (int i=1;i<=n;++i)
			if (!chk(p[i],p[i+1])){
				--ans;
				break;
			}
		for (int i=1;i<=n;++i)
			if (!chk(p[i],p[i-1])){
				--ans;
				break;
			}
		printf("%d\n",ans);
		exit(0);
	}
}
int dfs(int las,int t,int len,int pos,int mn){
	if (pos==len){
		if (abs(las-t)<=3 && chk(las,t)) return 1;
		return 0;
	}
	int res=0;
	for (int i=max(mn+1,las-3);i<=min(n-1,las+3);++i){
		if (!vis[i] && chk(las,i)){
			vis[i]=1;
			res+=dfs(i,t,len,pos+1,mn);
			vis[i]=0;
		}	
	}
	return res;
}
inline int get_val(int s,int t){
	vis[s]=vis[t]=1;
	int k=min(s,t);
	int res=dfs(s,t,n-k,2,k);
	vis[s]=vis[t]=0;
	return res;
}
int main(){
	n=read(),m=read(),k=read();
	for (int i=1;i<=m;++i){
		int u=n-read(),v=n-read();
		if (abs(u-v)<=k) a[u][v-u+3]=1;
	}
	if (n==1) return puts("1"),0;
	if (!k) return puts("0"),0;
	if (n==2) return puts(m?"0":"1"),0;
	if (k==1) return puts("0"),0;
	if (k==2) sub2::work();
	if (n<=7){
		if (chk(1,0)) ad(ans,get_val(0,1));
		if (chk(2,0)) ad(ans,get_val(0,2));
		if (n>=4 && chk(3,0)) ad(ans,get_val(0,3));
		printf("%d\n",ans);
		return 0;
	}
	for (int i=n-1;n-i<=7 && ~i;--i){
		g[i]=get_val(i+1,i);
		f[i]=get_val(i,i+1);
	}	
	for (int i=max(-1,n-8);~i;--i){
		f[i]=g[i]=0;
		if (chk(i,i+2)) ad(f[i],g[i+1]);
		if (chk(i,i+3)){
			if (chk(i+2,i+1)) ad(f[i],g[i+2]);
			if (chk(i+4,i+1)){
				if (chk(i+3,i+2) && chk(i+2,i+5)) ad(f[i],g[i+4]);
				if (chk(i+3,i+6) && chk(i+5,i+2) && chk(i+2,i+4)) ad(f[i],g[i+5]);
			}
		}
		if (chk(i+2,i)) ad(g[i],f[i+1]);
		if (chk(i+3,i)){
			if (chk(i+1,i+2)) ad(g[i],f[i+2]);
			if (chk(i+1,i+4)){
				if (chk(i+2,i+3) && chk(i+5,i+2)) ad(g[i],f[i+4]);
				if (chk(i+6,i+3) && chk(i+2,i+5) && chk(i+4,i+2)) ad(g[i],f[i+5]);
			}
		}
	}
	if (chk(1,0)) ad(ans,f[0]);
	if (chk(2,0)){
		if (chk(0,1)) ad(ans,f[1]);
		if (chk(0,3)){
			if (chk(4,1) && chk(1,2)) ad(ans,f[3]);
			if (chk(3,1) && chk(1,4) && chk(5,2)) ad(ans,f[4]);
		}
	}
	if (chk(3,0)){
		if (chk(0,1)){
			if (chk(1,2)) ad(ans,f[2]);
			if (chk(1,4)){
				if (chk(5,2) && chk(2,3)) ad(ans,f[4]);
				if (chk(4,2) && chk(2,5) && chk(6,3)) ad(ans,f[5]);
			}	
		}
		if (chk(0,2)){
			if (chk(2,1) && chk(1,4)) ad(ans,g[3]);
			if (chk(2,5) && chk(4,1) && chk(1,3)) ad(ans,g[4]);
		}	
	}
	printf("%d\n",ans);
	return 0;
}