自动搬运

查看原文

来自洛谷，原作者为

	QwQcOrZ AFOed | 印刷成文不能代表它们就是真理 | 极东魔术昼寝结社之夏 | The Great Gig In The Sky

搬运于2025-08-24 21:50:21，当前版本为作者最后更新于2020-09-21 14:37:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

考虑在无向图的生成树上dp（实际上是生成森林，因为可能会不连通，但为了方便讨论我们把它看成一棵树）

因为题设，所以树的深度不会超过 $10$，那么可以把当前节点到根的路径上的点的状态都压起来

设 $dp_{i,j}$ 表示当节点 $i$ 到根节点的路径上的点的状态为 $j$ 时，生成树中除了节点 $i$ 到根节点的路径上的点（也就是状态被压入 $j$ 的点），其它所有 $dfs$ 序比 $i$ 小的节点都被覆盖了的最小费用

其中 $j$ 表示的每个点的状态有三种：$0$ 表示选了，$1$ 表示不选但没被覆盖，$2$ 表示不选且已被覆盖

这个状态可能理解起来有点抽象，所以我画了张图：

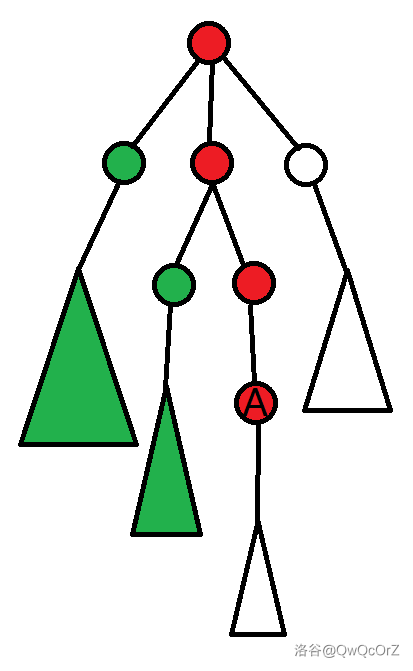
其中三角形表示子树，圆形表示节点，$A$ 点为当前处理到的点，红点为压入状态 $j$ 的点，绿点为要求被覆盖的点，白点为还未处理过的点

每次转移时从父亲节点的 $dp$ 值继承过来，选或不选分类讨论一下，对应更改状态即可

要注意的是每次 dfs 完儿子后要从儿子向上更新当前节点的 $dp$ 值，因为已经处理过的点如果不在状态内表示的话必须是被覆盖的

最后答案即为森林内每棵树的最优解之和

$Code\ Below$（我这里为了方便 $dp_{i,j}$ 中的 $i$ 表示的是深度）

#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5;
const int M=2.5e4+5;
const int D=15;
const int S=59059;
const int inf=1e9+7;

inline int read()
{
	register int s=0;
	register char c=getchar(),lc='+';
	while (c<'0'||'9'<c) lc=c,c=getchar();
	while ('0'<=c&&c<='9') s=s*10+c-'0',c=getchar();
	return lc=='-'?-s:s;
}
void write(register int x)
{
	if (x<0)
	{
		putchar('-');
		x=-x;
	}
	if (x<10) putchar(x+'0');
	else
	{
		write(x/10);
		putchar(x%10+'0');
	}
}
inline void print(const register int x,const register char c='\n')
{
	write(x);
	putchar(c);
}
struct edge
{
	int to,nxt;
}e[M*2];
int head[N],cnt=0;
void add(int u,int v)
{
	e[++cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
bool vis[N];
int a[N],dep[N],Pow[D],q[N],dp[D][S];//0:选了，1:不选且没覆盖，2:不选且覆盖 
inline int get(register int i,register int j)//返回i在三进制下的第j位
{
	return i/Pow[dep[j]]%3;
}
inline void up(register int &x,register int y)
{
	x=min(x,y);
}
void dfs(register int now)
{
	register int cnt=0;
	vis[now]=1;
	for (register int i=head[now];i;i=e[i].nxt)
	if (vis[e[i].to]&&dep[e[i].to]<dep[now])
	q[++cnt]=e[i].to;//把当前节点的所有返祖边存到q中
	if (dep[now]==0)
	{
		dp[0][0]=a[now];
		dp[0][1]=0;
		dp[0][2]=inf;
	}//如果是根节点则不需要从父亲继承dp值
	else
	{
		for (register int i=0;i<Pow[dep[now]+1];i++) dp[dep[now]][i]=inf;
		for (register int i=0;i<Pow[dep[now]];i++)//枚举父亲的状态
		{
			register int No=1,Yes=i;
            //No表示的是当前节点不选时，当前节点的状态
            //Yes表示的是当前节点选时，当前节点到根路径上所有节点的状态
			for (register int j=1;j<=cnt;j++)
			{
				if (get(i,q[j])==0) No=2;
                //当当前节点不选时，如果返祖边有连向被选的点，那么当前节点会被覆盖
				if (get(i,q[j])==1) Yes+=Pow[dep[q[j]]];
                //当当前节点选时，如果返祖边连向未被选且没有被覆盖的点，那么被连向的点会被覆盖
			}
			up(dp[dep[now]][i+No*Pow[dep[now]]],dp[dep[now]-1][i]);
			up(dp[dep[now]][Yes],dp[dep[now]-1][i]+a[now]);
		}
	}
	for (register int i=head[now];i;i=e[i].nxt)
	{
		register int to=e[i].to;
		if (vis[to]) continue;
		dep[to]=dep[now]+1;
		dfs(to);
		for (register int j=0;j<Pow[dep[to]];j++)
		dp[dep[now]][j]=min(dp[dep[to]][j],dp[dep[to]][j+2*Pow[dep[to]]]);
        //从儿子向上更新dp值
	}
}

signed main()
{
	Pow[0]=1;
	for (register int i=1;i<=10;i++) Pow[i]=Pow[i-1]*3;
	memset(vis,0,sizeof(vis));
	memset(dep,0,sizeof(dep));
	register int n=read(),m=read(),ans=0;
	for (register int i=1;i<=n;i++) a[i]=read();
	for (register int i=1;i<=m;i++)
	{
		register int u=read(),v=read();
		add(u,v);
		add(v,u);
	}
	for (register int i=1;i<=n;i++)
	if (!vis[i])
	{
		dfs(i);
		ans+=min(dp[0][0],dp[0][2]);
	}
	print(ans);

	return 0;
}

最后，此题卡常，记得开 O2