1 条题解
-
0
自动搬运
来自洛谷,原作者为

bztMinamoto
**搬运于
2025-08-24 21:50:13,当前版本为作者最后更新于2018-11-16 22:20:23,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
我是来帮楼下加藤大佬写题解的……全世界都没找到加藤大佬写法的说明……很难受……
首先我们把看成,看成,一个区间满足条件就意味着这个区间的所有前缀和都大于等于,所有后缀和都大于等于
我们记录一下前缀和,所有前缀和大于等于就是,所有后缀和都大于等于就意味着,即,然后因为已经在第一个条件里满足了,所以合起来就是,。用人话说,一个区间满足条件,那么这个区间内的都不小于且是这个区间中最大的数
于是我们定义,意思是中的所有数都大于等于,且为这个区间中最大的数,为所有满足条件的数中最靠右的。那么我们就可以枚举左端点,如果这个左端点肯定不行,否则这个左端点能匹配的最大的右端点就是
现在的问题就是怎么求出了,我们一开始先把所有的都赋值为,这样到时候可以少讨论一些边界情况。
首先,如果,即为,那么只能等于,因为它的下一个就小于它了。所以我们只考虑讨论为的情况
我们考虑从后往前做,定义为它后面的第一个与它相等的位置,记录一个指针,表示每一次的,现在做到了,那么应该是指在的位置。
那么转移会有两种情况
1.,那么直接转移即可
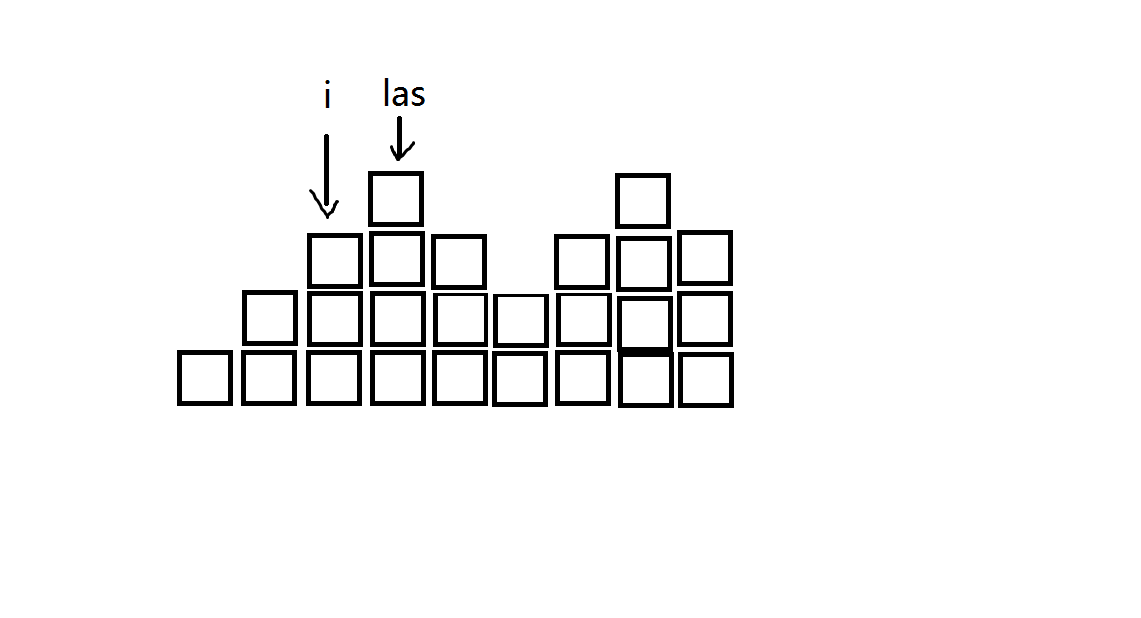 2.变大。比如图中,的位置才是
2.变大。比如图中,的位置才是
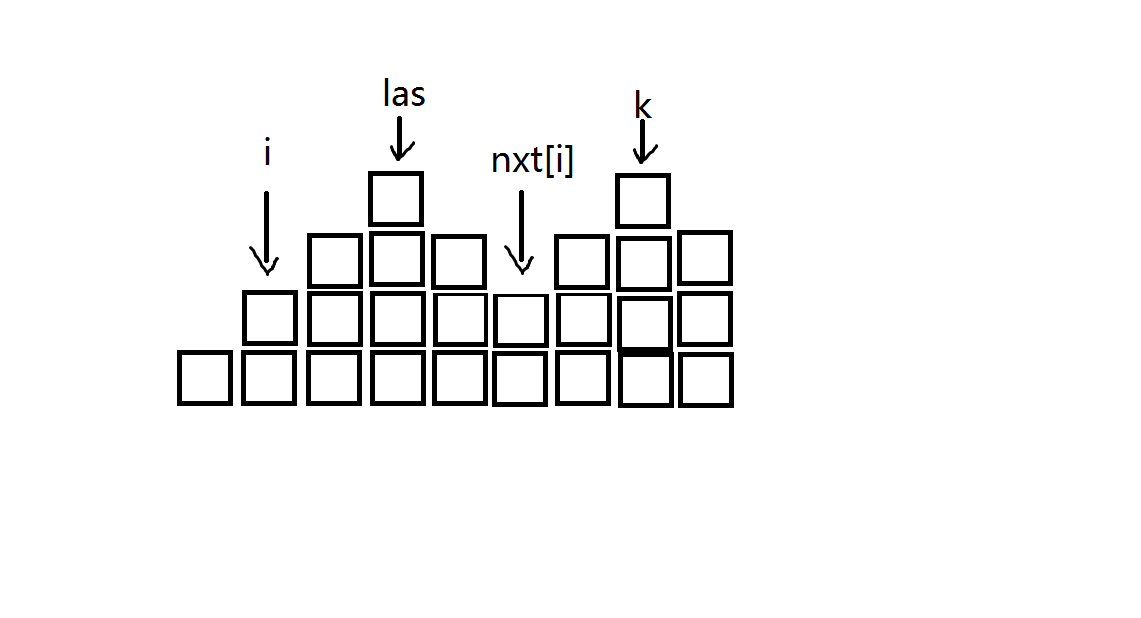 我们发现,在本题中,相邻两个数的值最多只会相差,于是若是存在如图的情况,那么必然存在。不难证明区间内的数肯定同时大于或同时小于,如果全都小于那么有,我们之前已经处理掉了。所以之间的数必然全都大于。因为已经求出来了,如果,我们可以把这一段给接上去,那么新的区间肯定还是满足条件的,且不难证明不存在比它更优的。这种情况下我们让指向并更新即可。
我们发现,在本题中,相邻两个数的值最多只会相差,于是若是存在如图的情况,那么必然存在。不难证明区间内的数肯定同时大于或同时小于,如果全都小于那么有,我们之前已经处理掉了。所以之间的数必然全都大于。因为已经求出来了,如果,我们可以把这一段给接上去,那么新的区间肯定还是满足条件的,且不难证明不存在比它更优的。这种情况下我们让指向并更新即可。只要处理出的所有的就可以了,最后的答案就是,时间复杂度
代码看楼下加藤大佬的好了
- 1
信息
- ID
- 2637
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
