1 条题解
-
0
自动搬运
来自洛谷,原作者为

Semsue
NOI2023 Ag搬运于
2025-08-24 21:50:11,当前版本为作者最后更新于2021-11-04 23:59:15,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
板子题:https://www.luogu.com.cn/problem/P3561
此题题意
给你定一个竞赛图,对每个点求出一条不重复经过点的路径,使其经过的点最多。。
竞赛图的一些性质
1,缩点之后是一条链
准确地说不是一条链,而是对于每个拓扑序在前的连通分量,都会向拓扑序再后的连通分量连边。由竞赛图的定义易知。
那么这么看这个性质就很显然了。任意两个拓扑序相邻的连通分量必有连边。
2,竞赛图必有哈密顿通路
这个可以构造证明,下文将会提到。
3,强连通竞赛图必有哈密顿回路。
这个也是构造证明,还是下文会提到。
做法
那么此题做法就很显然了,先缩点,然后对于每个强连通分量,求哈密顿回路。然后就可以对任意一个强连通分量任意点进,任意点出了。
那么重点是如何求哈密顿通路/回路。
这里给出一个 的构造。记 代表存在 到 的路径。
首先构造哈密顿通路,考虑增量构造。
假设我已经求出前 个点的一个哈密顿通路,考虑将 加入。设前面的哈密顿通路起点为 终点为 ,每个点 下一个点为 。如果 或者 那么直接将 加入这条链即可,将 或 设成 。
否则一定是下面这样:

那么显然一定存在一个 使得 。将 插到 之间,即令 即可。
至此我们完成了哈密顿通路的构造。时间复杂度 。
之后考虑强连通竞赛图的哈密顿回路,首先求出哈密顿通路,还是设起点为 ,终点为 。
考虑找到第一个 使得 ,也就是第一可以成环的位置,设为新的 。现在得到了一个环 。这里我们不把 这条边显示出来,也就是说 还是哈密顿通路上的下一个点。另外由于这个图是强连通的,所以一定可以找到这样一个 。
然后考虑加入 ,还是设为 。
如果 ,那么直接扩展即可。否则我们直接找到第一个 使得 ,那么我们可以简单地构造出下面这样的路径:
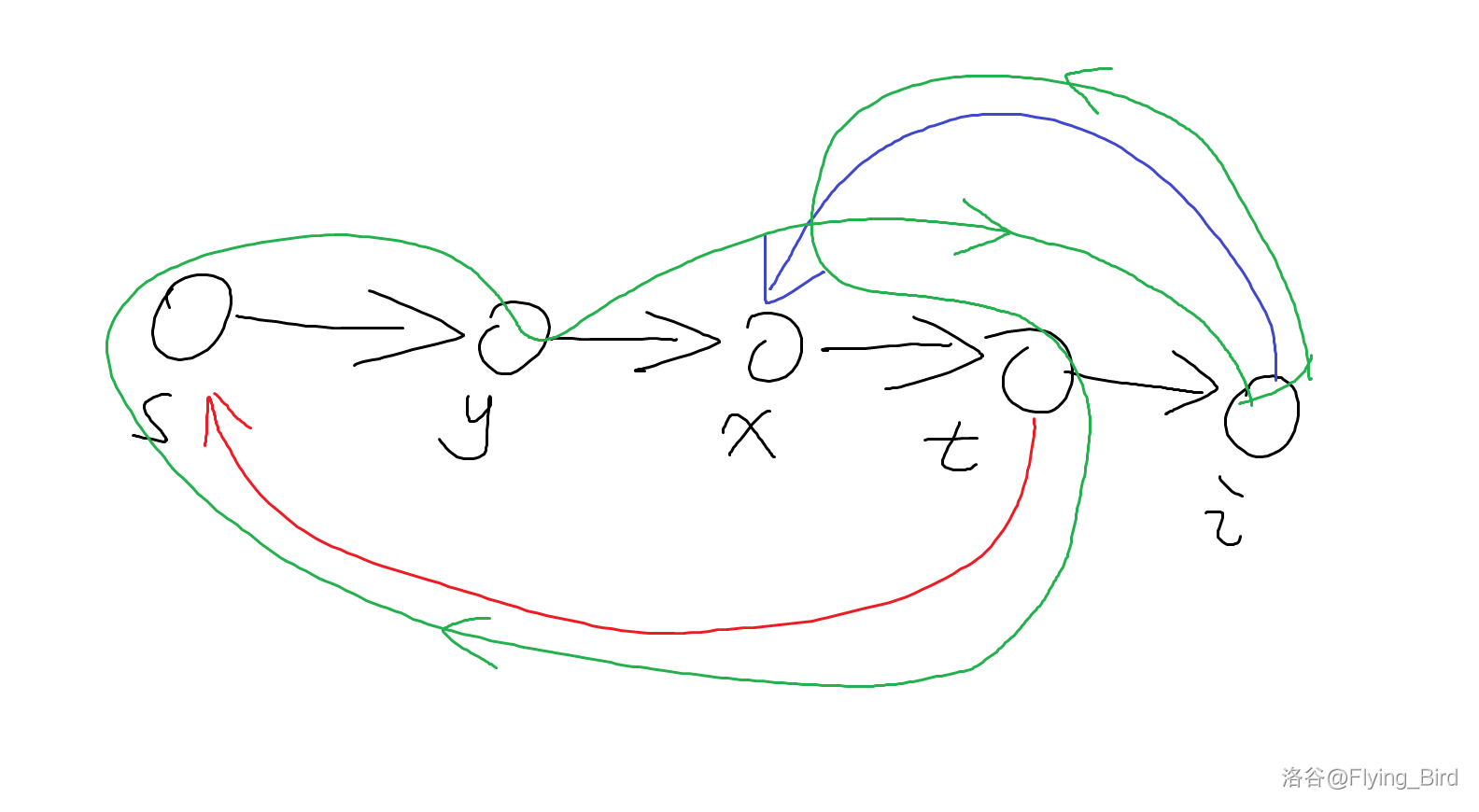
即设 的前一个是 ,那么构造 。此时为了保证 还是哈密顿通路上的点,我们令 ,修改 为原来的 , 为 即可。由于 是第一个 ,所以一定有 。
如果压根找不到 呢?仔细想想发现确实有这种情况,因为只有后继节点有一个连向前面那么就保证了强连通的性质。既然如此,那这些点不如直接摆烂,让后面那个点去往前连,如下图:
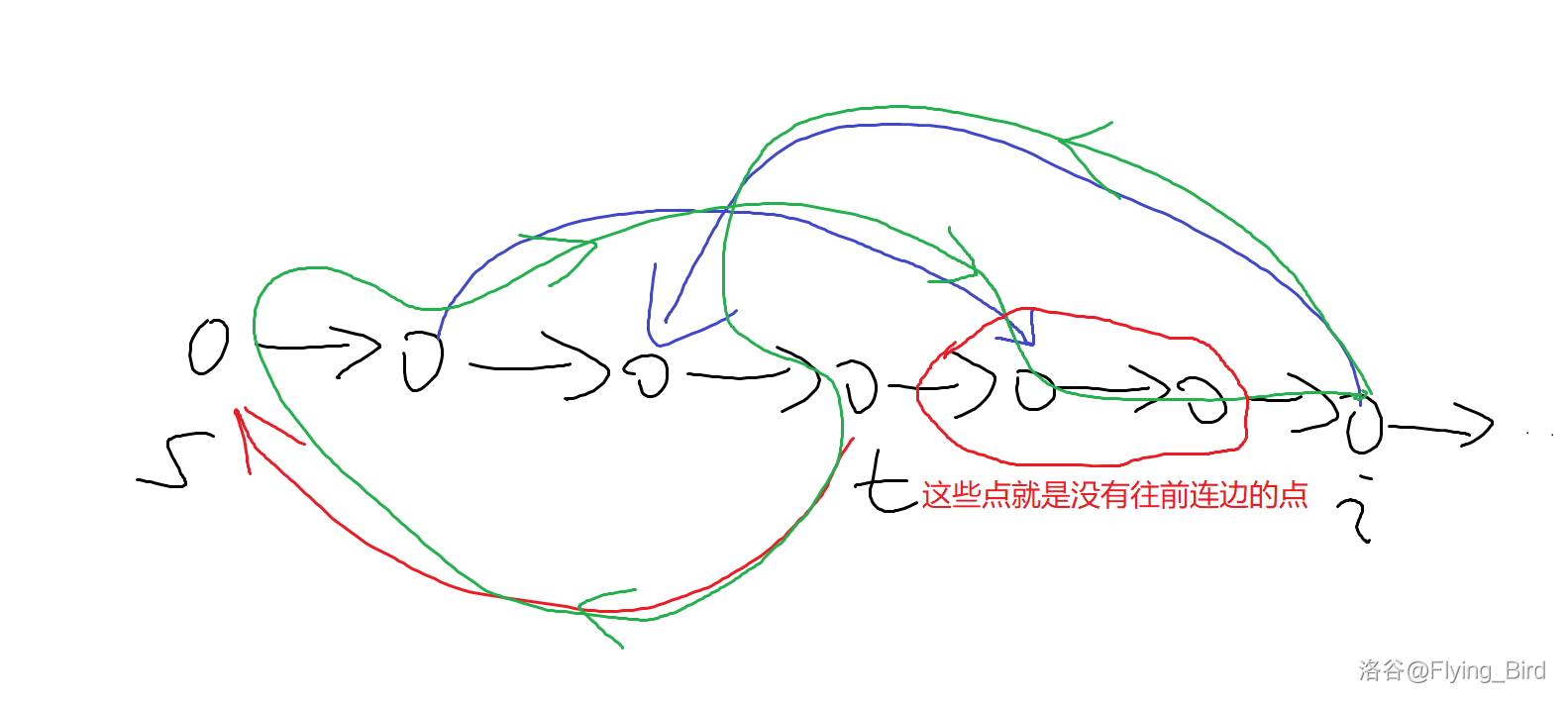
即 。注意这里这里 即 在哈密顿通路中的下一个点,即图中圆圈中最左边的点。然后和上面类似,只需把 修改为 ,这里 是原来的 。注意由于红圈中的点没有向前面连边,那么前面的每个点都会向其中的点连边,所以一定有 。
然后这样一直跑,由于强连通,所以 最后一定存在,所以一定会求出一条哈密顿回路其中的一条链,其中起点是 ,终点是 且 。
容易发现这个流程的复杂度为 。
好像可以做到更优复杂度,还是算了/qd。
参考代码
板子题:https://www.luogu.com.cn/problem/P3561
变量稍有不同。
#include <bits/stdc++.h> #define eb emplace_back using namespace std; const int maxn = 2005; template <typename T> void read(T &x) { T flag = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') flag = -1; for (x = 0; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; x *= flag; } int a[maxn][maxn]; int n, dfn[maxn], low[maxn], stk[maxn], col[maxn], top, Dfn, cnt; bool vis[maxn]; vector<int> vec[maxn], G[maxn], V[maxn], ans[maxn]; int in[maxn]; void tarjan(int u) { dfn[u] = low[u] = ++Dfn; stk[++top] = u; vis[u] = 1; for (int v : vec[u]) { if (!dfn[v]) { tarjan(v); low[u] = min(low[u], low[v]); } else if (vis[v]) low[u] = min(low[u], dfn[v]); } if (dfn[u] == low[u]) { cnt++; while (stk[top] != u){ col[stk[top]] = cnt; vis[stk[top]] = 0; top--; } col[u] = cnt; vis[u] = 0; top--; } } int nxt[maxn]; queue<int> q; void solve(int c) { // 求强连通分量 c 的一条哈密顿回路 // 先求一条哈密顿通路 if (V[c].size() == 1) return; int s = V[c][0], t = s; for (int i = 1; i < (int)V[c].size(); i++) { int x = V[c][i]; if (a[t][x]) nxt[t] = x, t = x; else if (a[x][s]) nxt[x] = s, s = x; else for (int j = s; j != t; j = nxt[j]) if (a[j][x] && a[x][nxt[j]]) { nxt[x] = nxt[j]; nxt[j] = x; break; } } t = 0; for (int i = nxt[s]; i != 0; i = nxt[i]){ if (t) { if (a[i][s]) { t = i; continue; } for (int j = s, k = nxt[s]; j != t; j = k, k = nxt[k]) { if (a[i][k]) { nxt[j] = nxt[t]; nxt[t] = s; s = k; t = i; break; } } } else if (a[i][s]) t = i; } nxt[t] = s; } int pos[maxn]; int main() { read(n); for (int i = 2; i <= n; i++) for (int j = 1, x; j <= i - 1; j++){ read(x); if (x) vec[j].eb(i), a[j][i] = 1; else vec[i].eb(j), a[i][j] = 1; } for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i); for (int i = 1; i <= n; i++) V[col[i]].eb(i); for (int i = 1; i <= n; i++) for (int j : vec[i]) if (col[i] != col[j]) G[col[i]].eb(col[j]), in[col[j]]++; for (int i = 1; i <= cnt; i++) if (!in[i]) q.push(i); top = 0; while (!q.empty()) { int u = q.front(); q.pop(); stk[++top] = u; pos[u] = top; for (int v : G[u]) { in[v]--; if (!in[v]) q.push(v); } } for (int i = 1; i <= top; i++) solve(stk[i]); for (int i = 1; i <= n; i++) { int lst = i, now = pos[col[i]]; while (1) { if (V[stk[now]].size() == 1) { ans[i].eb(lst); if (now == top) break; lst = V[stk[++now]][0]; continue; } ans[i].eb(lst); for (int x = nxt[lst]; x != lst; x = nxt[x]) ans[i].eb(x); if (now == top) break; lst = V[stk[++now]][0]; } } for (int i = 1; i <= n; i++) { printf("%d ", (int)ans[i].size()); for (int j : ans[i]) printf("%d ", j); puts(""); } return 0; }reference
https://www.cnblogs.com/TheRoadToTheGold/p/8439160.html#_label1
https://www.cnblogs.com/Hs-black/p/13749764.html
最后的最后

- 1
信息
- ID
- 4976
- 时间
- 2000ms
- 内存
- 250MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
