自动搬运

查看原文

来自洛谷，原作者为

	i207M 这个家伙很蠢，什么也没有留下

搬运于2025-08-24 21:50:04，当前版本为作者最后更新于2019-06-16 21:41:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

答案有3种可能的来源，分别是

注意到前两种都是可以一遍BFS得到的，我们来关注后一项：因为b很小，所以我们为了不走a，不惜多经过几条边。换句话说，我们要求一个“最短偶数路”长度

我们先考虑一个暴力：既然长度是偶数，我们每次走两步不就行了。先枚举u的出边v，再枚举v的出边w，如果u和w没有边，那么w就能被u更新到。

这样的复杂度显然是$O(m^2)$的，如何优化？

像这种枚举两层出边，可以联想到复杂度为$O(m\sqrt{m})$的三元环计数。观察，如果u更新了w，那么$(v,w)$这条边已经发挥了它作为第二条边的作用，我们直接将它删除即可。这可以用双向链表实现。

注意我们要开两个边表！第一层遍历的是原边表，第二层遍历的是可删的边表！

至于时间复杂度的证明的话，简单的想法就是一个三元环会被遍历三边，所以复杂度为$O(m\sqrt{m})$，而其他边遍历一次后就被删除了；POI官方给出了一个新颖的复杂度证明，有兴趣的同学可以看一下：

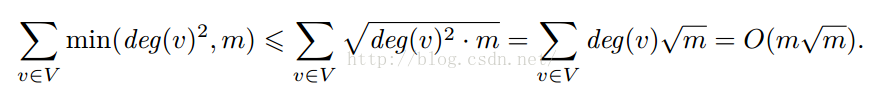
#define N 100005
struct Graph
{
    int head[N],cnte,pr[N*2],nx[N*2],v[N*2];
    il void adde(int uu,int vv)
    {
        v[++cnte]=vv,nx[cnte]=head[uu],pr[head[uu]]=cnte,head[uu]=cnte;
        v[++cnte]=uu,nx[cnte]=head[vv],pr[head[vv]]=cnte,head[vv]=cnte;
    }
    il void del(int x,int i)
    {
        nx[pr[i]]=nx[i],pr[nx[i]]=pr[i];
        if(head[x]==i) head[x]=nx[i];
    }
} G,H;
int n,m,S,a,b;
int d[N];
int q[N],hd,tl;
int ans[N];
bool vis[N];
signed main()
{
#ifdef M207
    freopen("in.in","r",stdin);
    // freopen("ot.out","w",stdout);
#endif
    in(n,m,S,a,b);
    for(ri i=1,uu,vv; i<=m; ++i)
    {
        in(uu,vv);
        G.adde(uu,vv),H.adde(uu,vv);
    }
    d[q[hd=tl=1]=S]=1;
    while(hd<=tl)
    {
        int x=q[hd++];
        for(ri i=G.head[x]; i; i=G.nx[i])
            if(!d[G.v[i]]) d[q[++tl]=G.v[i]]=d[x]+1;
    }
    for(ri i=1; i<=n; ++i)
    {
        if(d[i])
        {
            --d[i];
            ans[i]=min(a*d[i],b*(d[i]>>1)+a*(d[i]&1));
            d[i]=0;
        }
        else ans[i]=1e9;
    }
    d[q[hd=tl=1]=S]=1;
    while(hd<=tl)
    {
        int x=q[hd++];
        for(ri i=G.head[x]; i; i=G.nx[i]) vis[G.v[i]]=1;
        for(ri i=G.head[x]; i; i=G.nx[i])
        {
            int V=G.v[i];
            for(ri j=H.head[V]; j; j=H.nx[j])
            {
                if(d[H.v[j]]||vis[H.v[j]]) continue;
                d[q[++tl]=H.v[j]]=d[x]+1;
                H.del(V,j);
            }
        }
        for(ri i=G.head[x]; i; i=G.nx[i]) vis[G.v[i]]=0;
    }
    for(ri i=1; i<=n; ++i)
    {
        if(d[i]) ckmin(ans[i],b*(d[i]-1));
        out(ans[i]);
    }
    return 0;
}