自动搬运

查看原文

来自洛谷，原作者为

	RenaMoe 你好世界

搬运于2025-08-24 21:49:58，当前版本为作者最后更新于2019-09-28 10:14:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解 P3538 【[POI2012]OKR-A Horrible Poem】

题面

判断字符串循环节最方便的是$hash$

不会的请出门左转P3370

我们先把字符串$hash$一遍

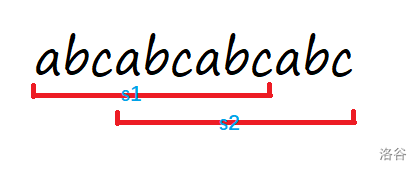
如图，如果设循环节长度为$3$时，$s1$和$s2$的$hash$值是相等的

所以只需要找最小的$len$使得$hash(l+len,r)=hash(l,r-len)$

另外，循环节的长度的循环次数都一定是总长的约数

我的做法是把总长除掉循环次数

先把$len$分解质因数

（线性筛质数，并记录下每个数的最小质因子加速分解，这已经是常规操作了）

因为最小循环节的倍数也是循环节

所以从$len$开始试除每个质因子并判断（你可以理解为$len$的因子分为循环节的因子和循环次数的因子，要把循环次数的因子除掉）

具体的看代码吧。。。

代码

#include <cstdio>
#include <cctype>
#include <vector>

using namespace std;

template<typename T> inline void read(T &x) {
	x = 0; T k = 1; char in = getchar();
	while (!isdigit(in)) { if (in == '-') k = -1; in = getchar(); }
	while (isdigit(in)) x = x * 10 + in - '0', in = getchar();
	x *= k;
}

typedef long long ll;

const ll MOD = 1e9 + 7;
const int N = 5e5 + 5;

int n, m;
ll g[N], hash[N], pow[N];// g记录最小质因子，pow存进制的整数次幂
char s[N];
bool vis[N];
vector<ll> pri;

// 线性筛
inline void euler() {
	for (ll i = 2; i <= n; ++i) {
		if (!vis[i])
			pri.push_back(i), g[i] = i;
		for (int j = 0; j < pri.size() && pri[j] * i <= n; ++j) {
			vis[pri[j]*i] = true, g[pri[j]*i] = pri[j];
			if (i % pri[j] == 0)
				break;
		}
	}
}

// 提取hash值
inline ll calc(int l, int r) {
	return ((hash[r] - hash[l-1] * pow[r-l+1]) % MOD + MOD) % MOD;
}

int main() {
	read(n);
	euler();
	scanf("%s", s+1);
    // hash
	for (int i = 1; i <= n; ++i)
		hash[i] = (hash[i-1] * 29 + s[i] - 'a' + 1) % MOD;
	
    // 预处理整数次幂
	pow[0] = 1;
	for (int i = 1; i <= n; ++i)
		pow[i] = (pow[i-1] * 29) % MOD;

	read(m);
	while (m--) {
		int l, r, len, ans;
		read(l), read(r), ans = len = r - l + 1;
        // 一点点常数优化
		if (calc(l+1, r) == calc(l, r-1)) {
			puts("1");
			continue;
		}
        // 重点
		while (len > 1) {
			if (calc(l+ans/g[len], r) == calc(l, r-ans/g[len]))// 判断
				ans /= g[len];// 除掉循环次数的因子
			len /= g[len];//分解
		}
		printf("%d\n", ans);
	}
    return 0;
}