自动搬运

查看原文

来自洛谷，原作者为

	lgnotus 弈星本命

搬运于2025-08-24 21:49:56，当前版本为作者最后更新于2021-07-15 16:24:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

思路

UPD:$\text{2021/7/17}$ ：把爆炸的图补上了

这题的样例给的很好，我们先把图画出来。

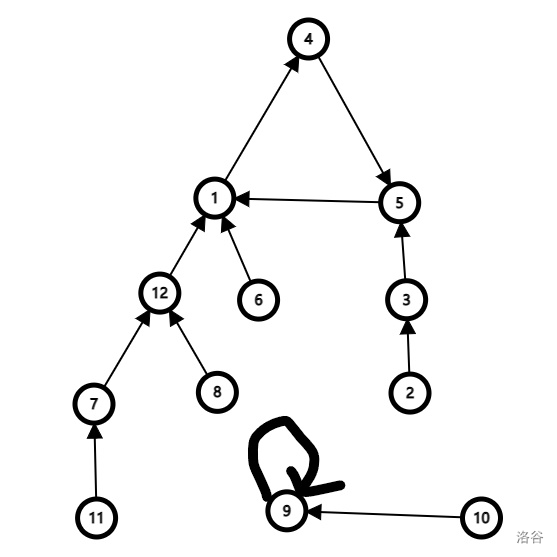
结合图像与题意，此图为内向基环森林，存在自环。下面分三种情况对两个结点 $u$、$v$ 进行讨论:

$\text{u}$、$\text{v}$ 不在同一棵基环树上

• 此种情况对应上图结点 9、11，我们发现他们无论怎么走都不可能走到一起，输出 -1 -1。这里提供两种方法判断两点是否在同一棵基环树上

• 利用并查集维护连通性（我刚开始也是这么做的，但是发现在统计环长的时候可以同时处理，详见下）

• 判断两个点所在树的根节点是否在同一个环上，topu 找环对于环上结点遍历一遍即可，同时也可处理出环长 $u$、$v$ 在同一棵基环树上且位于环上同一结点的子树内

$\text{u}$、$\text{v}$ 在同一棵基环树上且在环上同一结点的子树内

• 此种情况对应图上结点 11、8，此时两结点 LCA 即为答案，因为基环树树剖求 LCA 较为麻烦，所以我们采取倍增的方式
• 简单口胡证明：
  • 如果答案非 LCA，则必然在 LCA 的祖先结点或环上结点，但这样 x、y 都会增加，不会使答案更优，毫无裨益。
• 建反图，对于环上结点向其子树跑 dfs，将每一个节点打上“属于哪个根”的标记，即可判断两个节点是否在同一棵子树

$\text{u}$、$\text{v}$ 在同一颗基环树上且在环上不同结点的子树内

• 此种情况对应图上结点 11、2 ，此时相遇点必为两点所在树的根节点（记为 fu、fv）其中之一，我们需要求出在其中一点相遇时的答案根据题意取最优解即可
• 简单口胡证明：
  • 同上，如果答案非 fu 或 fv 而在其中一棵子树的结点处，则不能满足 $\max(u,v)$ 最小的条件，如答案在环上结点，则 x、y 都会增加，毫无裨益

拓扑排序找环即可

code

我人菜代码写的有些难看（

必写快读！！！

#include<bits/stdc++.h>
#define N 500010
using namespace std;

int cnt[N],n,m,book[N],fa[N][21],de[N],len[N],book2[N],step[N],tot;
vector<int>e[N];
queue<int>q;


void dfs(int u,int f,int rt,int d){
    de[u]=d;book[u]=rt;
    for(int i=0;i<e[u].size();i++){
        int v=e[u][i];
        if(cnt[v]||v==f)continue;
        dfs(v,u,rt,d+1);
    }
}

void pre(){
for(int p=1;p<=19;p++)
    for(int i=1;i<=n;i++){    
        fa[i][p]=fa[fa[i][p-1]][p-1];
    }
}

int lca(int x,int y){
    if(de[x]<de[y])swap(x,y);
    int tmp=de[x]-de[y];
    for(int i=19;i>=0;i--)if(tmp>>i&1)x=fa[x][i];
    if(x==y)return y;
    for(int i=19;i>=0;i--){
        if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
    }
    return fa[x][0];
}

void doit(int u,int id,int az){
    if(step[u])return;
    book2[u]=id;len[id]++;step[u]=az;
    doit(fa[u][0],id,az+1);
}

bool check(int a,int b,int c,int d){
    if(max(a,b)!=max(c,d))return max(a,b)<max(c,d);
    if(min(a,b)!=min(c,d))return min(a,b)<min(c,d);
    return a>=b;
}

signed main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        int u;scanf("%d",&u);
        e[u].push_back(i);
        fa[i][0]=u;
        cnt[u]++;
    }
    for(int i=1;i<=n;i++)if(!cnt[i])q.push(i);
    while(!q.empty()){
        int u=q.front();q.pop();
        int v=fa[u][0];
        cnt[v]--;
        if(!cnt[v])q.push(v);
    }
    for(int i=1;i<=n;i++){
        if(cnt[i]){
            dfs(i,0,i,0);
            if(!step[i])doit(i,++tot,1);
        }
    }
    pre();
    while(m--){
        int u,v;scanf("%d%d",&u,&v);
        if(book2[book[u]]!=book2[book[v]]){
			cout<<-1<<' '<<-1<<endl;
		}else if(book[u]==book[v]){
            int LCA=lca(u,v);
            cout<<de[u]-de[LCA]<<' '<<de[v]-de[LCA]<<endl;
        }else{
        	int t1=book[u],t2=book[v];
            int ans1=de[u]+(step[t2]-step[t1]+len[book2[t1]])%len[book2[t1]],ans2=de[v]+(step[t1]-step[t2]+len[book2[t1]])%len[book2[t1]];
			if(check(de[u],ans2,ans1,de[v]))cout<<de[u]<<' '<<ans2<<endl;
            else cout<<ans1<<' '<<de[v]<<endl;
        }
    }
	return 0;
}
/*
10 10
2 1 10 3 4 5 6 7 8 10
1 2
*/