自动搬运

查看原文

来自洛谷，原作者为

	nawuxika **

搬运于2025-08-24 21:49:31，当前版本为作者最后更新于2021-05-26 23:12:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

分析

首先我们画下样例的图：

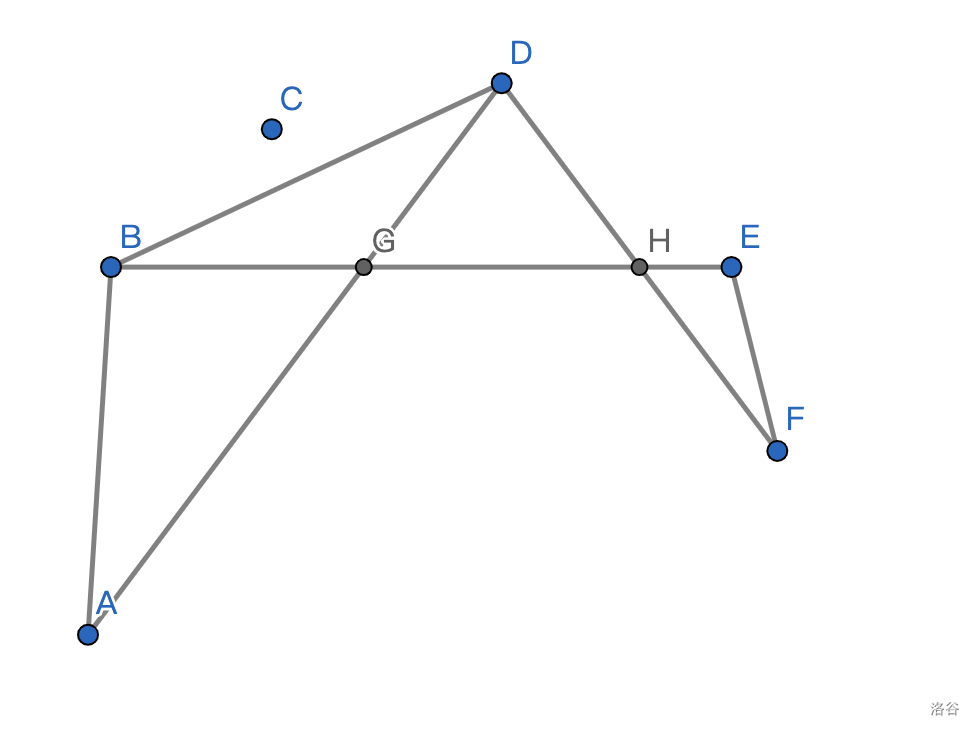
可以非常明显地看出最优路径是 $A \rightarrow G \rightarrow H \rightarrow F$。也就是说最优路径就是沿着剩下的 最内侧 的边行走。

其实作为一个 $\text{OI}$ 选手猜出结论就可以了。

证明

使用数学归纳法证明，归纳命题为：最内侧路径上的点数等于 $n$(不包括 $2$ 个端点) 时，最内侧路径是最短路径。

① 当 $n=0$ 即最内侧路径为一条线段时，命题成立。（两点间线段距离最短）

② 令当 $n = k$ 时命题成立，当 $n=k+1$ 时，取出最内侧路径和任意一条外侧路径，如下图所示：

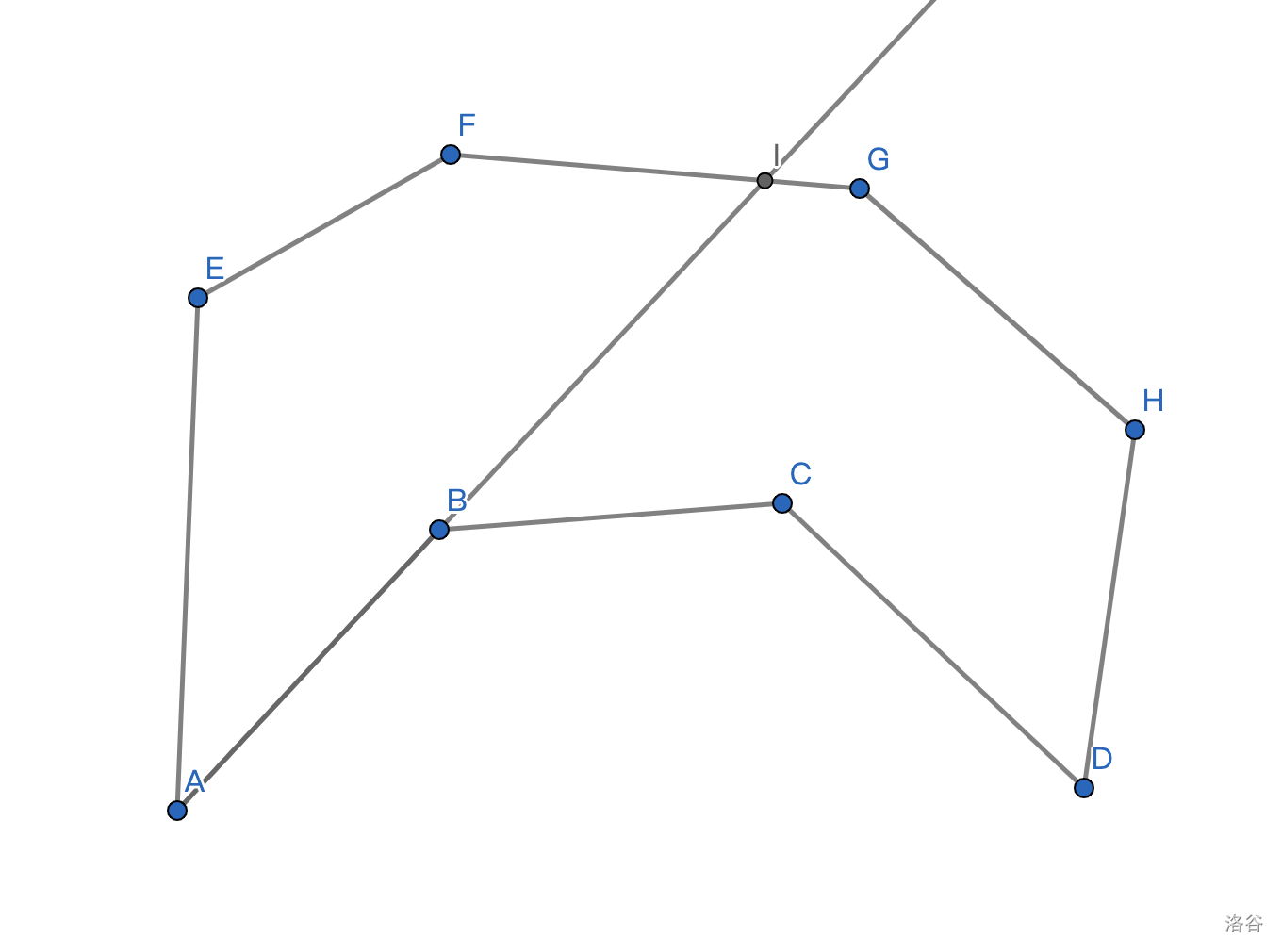
延长内侧路径第一条边将外侧路径分为两段，则有：

由于 $B \rightarrow I \rightarrow G \rightarrow G \rightarrow D$ 相对于 $B \rightarrow C \rightarrow D$ 为一个外侧路径且内侧路径除端点点数为 $k$，所以有：

综上，有：

则当 $n=k+1$ 时命题成立。

综合① ② 可知命题成立。结论成立。

可以看出最短路径其实可以跑一个半平面交得出，就样例而言，所求折线 $A \rightarrow G \rightarrow H \rightarrow F$ 即可视为四边形 $AGHF$ 的周长减去 $AF$。而 $AGHF$ 即可视为是 $\vec{AB},\vec{AD},\vec{BD},\vec{BE},\vec{DF},\vec{EF}$ 的右侧半平面的交集。

算法

朴素算法就是将所有剩下的边直接暴力跑一次半平面交，复杂度 $O((n^2-m)\log(n^2-m))$，由于 $n \le 10^5$，显然这种做法是需要优化的，可以发现对于每一个点，以它为起点的向量中只有最向内偏的向量是有效的，同时我们发现 $m \le 10^6$，那么我们可以考虑利用链式前向星存储所有不合法的边，然后对于每一个边，从后向前遍历找出最内侧的合法边。最后跑一遍半平面交，算个长度。完结散花。

$\text{AC CODE}$

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<set>
#include<bitset>
#include<map>
#include<algorithm>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#define ll long long
#define ui unsigned int
#define ull unsigned long long
#define il inline
using namespace std;
template<typename T>
il void read(T &x)
{
    x=0;int f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();}
    while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48); ch=getchar();}
    x*=f;
}
template<typename T>
il void write(T x)
{
    if(x<0) {putchar('-');x=-x;}
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int maxn=1e5+10,maxm=1e6+10;
const double eps=1e-12;//注意本题卡精度
int n,m,cnt,tot,top,head[maxn],h=1,t;
double ans;
bool vis[maxn],flag;
struct Edge{
    int to,next;
}edge[maxm<<1];
il void add(int u,int v)
{
    edge[++cnt].next=head[u];
    edge[cnt].to=v;
    head[u]=cnt;
}
struct point{
    double x,y;
    friend il point operator + (point a,point b) {return (point){a.x+b.x,a.y+b.y};}
    friend il point operator - (point a,point b) {return (point){a.x-b.x,a.y-b.y};}
    friend il point operator * (point a,double t) {return (point){t*a.x,t*a.y};}
}p[maxn],a[maxn];
il double d(point a,point b) {return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
il double dot(point a,point b) {return a.x*b.x+a.y*b.y;}
il double csp(point a,point b) {return a.x*b.y-b.x*a.y;}
il int sign(double x) {return fabs(x)<=eps?0:(x>0?1:-1);}
struct line{
    point p,v;
    double ang;
    friend il bool operator < (line a,line b)
    {return sign(a.ang-b.ang)==0?csp(a.v-a.p,b.v-a.p)>0:sign(a.ang-b.ang)<0;}
    il void getang() {ang=atan2(v.y-p.y,v.x-p.x);}
}l[maxn],q[maxn];
il point inter(line a,line b)
{
    point p1=a.p,p2=b.p,v1=a.v,v2=b.v,u=p2-p1;
    v1=v1-p1;v2=v2-p2;
    return p2+v2*(csp(u,v1)/csp(v1,v2));
}
il bool judge(line a,line b,line c)
{
    point p=inter(a,b);
    return sign(csp(c.v-c.p,p-c.p))<=0;
}
int main()
{
    read(n);read(m);
    for(int i=1;i<=n;++i) scanf("%lf%lf",&p[n-i+1].x,&p[n-i+1].y);//个人习惯是逆时针存图
    for(int i=1;i<=m;++i)
    {
        int u,v;read(u);read(v);
        if((u==1 and v==n) or (u==n and v==1)) flag=false;
        u=n-u+1;v=n-v+1;add(u,v);add(v,u);
    }
    if(flag) {cout<<d(p[1],p[n]); return 0;}//注意特判
    for(int i=1;i<n;++i)
    {
        for(int j=head[i];j;j=edge[j].next)
        {
            int v=edge[j].to;
            vis[v]=1;//处理出不合法的边
        }
        for(int j=n;j>i;--j)
        {
            if(!vis[j])
            {
                l[++tot].p=p[i];l[tot].v=p[j];
                l[tot].getang();break;
            }
        }
        for(int j=head[i];j;j=edge[j].next) vis[edge[j].to]=0;
    }
    l[++tot].p=p[n]; l[tot].v=p[1]; l[tot].getang();
    sort(l+1,l+tot+1);
    cnt=0;
    for(int i=1;i<=tot;++i)
    {
        if(i==1 or l[i].ang-l[i-1].ang>0) ++cnt;
        l[cnt]=l[i];
    }
    q[++t]=l[1];
    for(int i=2;i<=cnt;++i)
    {
        while(t>h and judge(q[t-1],q[t],l[i])) --t;
        while(t>h and judge(q[h],q[h+1],l[i])) ++h;
        q[++t]=l[i];
    }
    while(t>h and judge(q[t-1],q[t],q[h])) --t;
    while(t>h and judge(q[h],q[h+1],q[t])) ++h;
    tot=0;
    q[t+1]=q[h];
    for(int i=h;i<=t;++i) a[++tot]=inter(q[i],q[i+1]);
    a[tot+1]=a[1];
    for(int i=1;i<=tot;++i) ans+=d(a[i],a[i+1]);
    ans-=d(p[1],p[n]);
    printf("%.10lf",ans);
    return 0;
}