自动搬运

查看原文

来自洛谷，原作者为

	pythoner713 Hope deferred maketh the something sick.

搬运于2025-08-24 21:49:26，当前版本为作者最后更新于2021-01-26 17:01:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

将数组 $a,b$ 间下标相等或值相等的两个数连在一起：

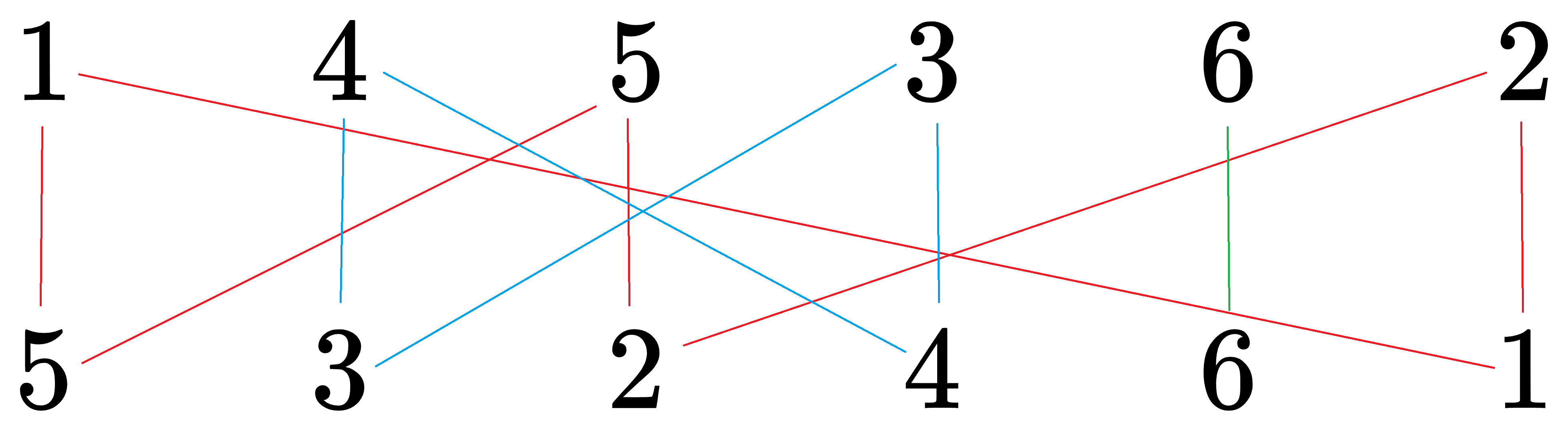
发现可以组成三个“环”：$(1,2,5),(3,4),(6)$

这些环互不影响，可以逐个击破。

对于长度为 $L$ 的环，注意到可以通过恰好 $L-1$ 次交换使得环内每个数都归位。为了使总代价最小，我们先找出环内代价最小的数，然后依次将它与本应在它位置上的数交换，如此交换 $L-1$ 次便可使环内所有数归位。

按照上述策略还原一个环的代价是：$\text{sum}+\min_1\times(L-2)$

$\text{sum}$ 为环内代价和，$\min_1$ 为那个最小的代价。

但是，如果环内每个数代价都很大，就需考虑另一种策略：先找出所有数中代价最小的数，先将它与环内代价最小的数交换（相当于在环外搬救兵，找全局最小代替环内最小）。经 $L-1$ 次交换将环内的数复原后，再将全局最小与环内最小替换回来。

按照这种策略，还原一个环的代价是：$\text{sum}+\min_1+\min_2\times(L+1)$

这里的 $\min_2$ 是全局最小代价。

对于每个环无非就是上述两种策略，取代价小者加起来即可。

#include<bits/stdc++.h>
#define int long long
#define nb 1000010
using namespace std;

int n, ans, min2 = 2e9, a[nb], b[nb], A[nb], w[nb];
bool vis[nb];

void work(int x){
	int len = 0, sum = 0, min1 = 2e9;
	while(!vis[x]){
		vis[x] = 1;					// 标记当前环内的数
		sum += w[a[x]];				// 累加当前环代价和
		min1 = min(min1, w[a[x]]);	// 找出环内最小代价
		x = A[b[x]];				// 跳至环内下一个数
		len++;						// 统计当前环的长度
	}
	int p = sum + min1 * (len - 2); // 策略一
	int q = sum + min1 + min2 * (len + 1); // 策略二
	ans += min(p, q);
}

signed main(){
	cin >> n;
	ios::sync_with_stdio(0);
	for(int i = 1; i <= n; i++) cin >> w[i], min2 = min(min2, w[i]);
	for(int i = 1; i <= n; i++) cin >> a[i], A[a[i]] = i;	// 将值映射到 a 的下标
	for(int i = 1; i <= n; i++) cin >> b[i];
	for(int i = 1; i <= n; i++) if(!vis[i]) work(i);		// 找到新环，逐个击破
	cout << ans;
	return 0;
}

最后顺便提一提，对于数组内交换的题，拆分成环考虑是常见的套路。可以顺便看看这两题：

P1667 数列

P4778 Counting swaps