自动搬运

查看原文

来自洛谷，原作者为

	Blithe_C A uncaring spirit, or is she?

搬运于2025-08-24 21:49:24，当前版本为作者最后更新于2022-07-18 05:26:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

一道烧脑的树上优化问题. 目前的几篇题解并没有把关键想法以及定义说得足够清楚，而且这个优化思路值得一看，因此写一篇新的题解.

---

简明题意：在一棵树上安装尽可能少的灭火器，希望其影响范围覆盖整棵树. 每个灭火器的影响节点数目和半径有限制. 求出最少的灭火器数.

形式化题意：给定正整数 $n,s,k$ 和一棵 $n$ 节点的树 $T$. 定义一个灭火器 $E$ 为一个二元组 $(loc, range)$，其中位置 $loc$ 是 $T$ 的一个节点，管辖范围 $range$ 是元数 $\leq s$ 的点集，其每个点（称其被 $E$ 管辖）都在 $T$ 上且与 $loc$ 间的路径长皆不超过 $k$. 你可以构造 $m$ 个灭火器并任意指定其位置和管辖范围，求最小的 $m$ 使得所有灭火器的管辖范围之并为 $T$ 的全体节点.

数据范围：$1\leq s\leq n\leq 10^5$，$1\leq k \leq 20$.

本题样例图示：.

---

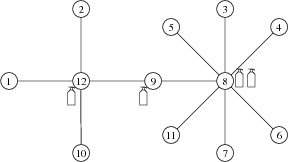首先，我们免不了任选一个根对树 DFS（这边采用后根周游），此过程中可能以树上 DP 的方式更新答案.

每个节点 $pos$ 的子问题是什么？目标是在 $pos$ 上放灭火器，但是需要最优地放置.

$s$ 和 $k$ 分别约束了灭火器的影响数量和半径，可从其入手. 由于一个节点可以放多个灭火器，而相对位置是确定的，试着优先卡 $k$ 的界，即尽量在距离（路径长）达到 $k$ 时放灭火器. 很自然地，需要知道 $pos$ 的子树中与其距离为 $k$ 的点有多少个，故用二维变量 $neibs(pos, dist)$ 记录 $pos$ 的子树中与其距离为 $dist$ 的点数，DFS 时递推更新.

因为不希望同一个节点被多个灭火器管辖，新增的灭火器管辖的点应该“扣除”掉，故需要一个动态量. 改用变量 $unasn(pos, dist)$ 表示子树中与 $pos$ 距离为 $dist$ 的未被管辖点数. 假设在当前位置 $unasn(pos, k)>0$，则必须在 $pos$ 新增 $d=\lceil\frac{unasn(pos, k)}{s}\rceil$ 个灭火器.

---

接下来，一种平凡的贪心思路就是把 $unasn(pos, k)$ 内的点全部扣除，然后从远到近分配子树里刚放置的灭火器的剩余可管辖点数 $d×s-unasn(pos, k)$，并扣除直到其为 $0$.

这样合适吗？

且不说这样剩余管辖权可能扣不完，一个点的灭火器除了可以管辖 DFS 正向的子树，还可以管到反向的那棵子树，这同样需要斤斤计较.

所以之前安装过的灭火器之后仍需定位和更新，于是引入第二个动态变量 $margin(pos, dist)$ 表示子树中与 $pos$ 距离为 $dist$ 的灭火器的剩余可管辖点数. 平凡思路也不能用，暂时只把 $pos$ 处的灭火器分配给 $unasn(pos, k)$ 这些点.

---

一句预警，下面贪心策略的最优性证明不仅我不会，而且网上也没找到，应该不是三言两语的问题. 贪心方法很多时候是微妙的，我们好做的只是直觉上理解为什么它好、以及说明其它策略没有它优.

下边是两个主要观察：

i) 为处理一个位于 $p$ 的灭火器管辖反向子树的情况，只需处理 $p$ 与其具有共同 LCA 的那些子树中未被管辖点的关系. 换言之，DFS 到一个位置 $pos$ 时，要考虑子树间管辖权的分配.

ii) 我们仍想「尽量只管与灭火器相距 $k$ 的点」，那就将其实施下去. 记 $D(u, v)$ 为节点距离，我们寻找子树间这样的点对 $x, y$，其满足 $D(x, pos)+D(pos, y)=k$，且 $x$ 位置有没耗尽管辖权的灭火器且 $y$ 点还没被管辖. 除非 $x$ 和 $y$ 在一棵子树上，否则 $k=D(x, pos)+D(pos, y)=D(x, y)$. 然后把 $x$ 位的灭火器管辖权分给 $y$，即让 $margin(pos, D(x, pos))$ 和 $unasn(pos, D(pos, y))$ 值同时减小至一个为 $0$.（注意 $D(x, pos)=0$ 就是前面分配 $pos$ 处灭火器的情况.）

换言之，我们需要在每个 $pos$ 处合并所有子树的信息，然后枚举子树间节点的“中间距离” $D(x, pos)$ 作上述更新：

using std::min;

int nodes, capacity, reach; // n, s, k
vector<vector<int>> edge, unassigned, margin; // unassigned 即 unasn
int count = 0; // 统计灭火器

inline int ceil_div(int above, int below){
	return (above+below-1)/below;
}

void travel_and_assign(int pos, int prev){
	unassigned[pos][0] = 1;
	for(auto &neib: edge[pos]){ // 遍历子节点
		if(neib==prev) continue;
		travel_and_assign(neib, pos);
		for(int dist = 1; dist<=reach; ++ dist){
			unassigned[pos][dist] += unassigned[neib][dist-1];
			margin[pos][dist] += margin[neib][dist-1]; margin[pos][dist] = min(margin[pos][dist], nodes); // 灭火器可管辖点数超过 nodes 时，无意义
		}
	}
	if(unassigned[pos][reach]>0){ // 决定在 pos 处放灭火器
		int employed = ceil_div(unassigned[pos][reach], capacity);
		count += employed;
		margin[pos][0] = min(employed*capacity, nodes);
	}
	for(int dist = 0; dist<=reach; ++ dist){ // 枚举中间距离并“再分配”
		int offset = min(unassigned[pos][reach-dist], margin[pos][dist]);
		unassigned[pos][reach-dist] -= offset; margin[pos][dist] -= offset;
	}
}

这基本是正解了，可得 ${\rm 20\,pts}$，还需亿些修改.

i) 根节点要特殊处理.

因为之前在每个 $pos$ 都没有把灭火器的管辖分配彻底，必须给最后剩下的全部未被管辖点分配. 对应的改动是，上面代码中的 reach-dist 需要改成一个从 reach-dist 枚举到 0 的循环变量. 有可能分完还有未被管辖点，则最后在根节点补灭火器解决. ${\rm 60\,pts}$.

ii) 如上所说，每个 $pos$ 都没有把灭火器的管辖分配彻底，影响最优性.

这里是此贪心法最微妙的地方.

我们也不愿意在每个 $pos$ 像根节点那样彻底分配，直到子树不留未被管辖点，这样会浪费管辖半径. —— 实际上本人这样写竟通过了本题，${\rm 326\,ms}$，似乎数据较水，但样例的输出是错的......

我们可以做个折衷，前面将子树内所有灭火器的管辖权分给了与其距离为 $k$ 的点，现在我们再分给“次必要”的与其距离为 $k-1$ 的点：考虑 $pos$ 子树内满足 $D(x, pos)+D(pos, y)=k-1$ 的点 $x, y$，当 DFS 跳到 $pos$ 的前驱 $pos'$ 时，$D(x, pos')+D(pos', y)=(k-1)+2=k+1>k$，故 $x$ 和 $y$ 如果不在 $pos$ 处理就无法再在 $pos'$ 同法处理.

即递归中要再加一条枚举：

	for(int dist = 0; dist<=reach-1; ++ dist){
		int offset = min(unassigned[pos][reach-1-dist], margin[pos][dist]);
		unassigned[pos][reach-1-dist] -= offset; margin[pos][dist] -= offset;
	}

如此可通过本题，${\rm 794\,ms}$.

算法的时间复杂度 $O(kn)$，空间复杂度 $O(kn)$.

本题最大的看点在于设计子问题（DP 状态）以及对贪心原则的坚持.

---

完整代码. 不嫌累式码风警告.

#include <bits/stdc++.h>

#define IOS_SPEED std::ios::sync_with_stdio(false)

using std::cin, std::cout;
using std::vector;
using std::min;

using lli = long long;

int nodes, capacity, reach;
vector<vector<int>> edge;

inline int ceil_div(int above, int below){
	return (above+below-1)/below;
}

void travel_and_assign(int pos, int prev, vector<vector<int>> &unassigned, vector<vector<int>> &margin, int &count){
	unassigned[pos][0] = 1;
	for(auto &neib: edge[pos]){
		if(neib==prev) continue;
		travel_and_assign(neib, pos, unassigned, margin, count);
		for(int dist = 1; dist<=reach; ++ dist){
			unassigned[pos][dist] += unassigned[neib][dist-1];
			margin[pos][dist] += margin[neib][dist-1]; margin[pos][dist] = min(margin[pos][dist], nodes);
		}
	}
	if(unassigned[pos][reach]>0){
		int employed = ceil_div(unassigned[pos][reach], capacity);
		count += employed;
		margin[pos][0] = min(employed*capacity, nodes);
	}
	for(int dist = 0; dist<=reach; ++ dist){
		int offset = min(unassigned[pos][reach-dist], margin[pos][dist]);
		unassigned[pos][reach-dist] -= offset; margin[pos][dist] -= offset;
	}
	for(int dist = 0; dist<=reach-1; ++ dist){
		int offset = min(unassigned[pos][reach-1-dist], margin[pos][dist]);
		unassigned[pos][reach-1-dist] -= offset; margin[pos][dist] -= offset;
	}
}

int least_extinguishers(){
	int ret = 0;
	auto unassigned = vector(nodes+1, vector<int>(reach+1, 0)), margin = vector(nodes+1, vector<int>(reach+1, 0));
	travel_and_assign(1, 0, unassigned, margin, ret);
	for(int dist = 0; dist<=reach; ++ dist){
		for(int other = reach-dist; other>=0; -- other){
			int offset = min(unassigned[1][other], margin[1][dist]);
			unassigned[1][other] -= offset; margin[1][dist] -= offset;
		}
	}
	int rest = 0;
	for(int dist = 0; dist<=reach; ++ dist) rest += unassigned[1][dist];
	ret += ceil_div(rest, capacity);
	return ret;
}

void interface(){
	cin >> nodes >> capacity >> reach;
	edge.resize(nodes+1);
	for(int i=0; i<nodes-1; ++i){
		int X, Y; cin >> X >> Y;
		edge[X].emplace_back(Y); edge[Y].emplace_back(X);
	}
	cout << least_extinguishers() << "\n";
	edge.clear();
}

int main()
{
	IOS_SPEED;
	interface();
	return 0;
}