自动搬运

查看原文

来自洛谷，原作者为

	nofind 苟到省选退役的蒟蒻

搬运于2025-08-24 21:49:24，当前版本为作者最后更新于2019-06-06 14:37:29，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意：

给出一个N个点的树,找出一个点来,以这个点为根的树时,所有点的深度之和最大。

解析：

首先暴力的做法就是对于每个点都用dfs求一遍,之后比较大小。

但是我们发现实际上对于x我们可以用它的父亲节点推出它的答案。

如图：

以5为根时：

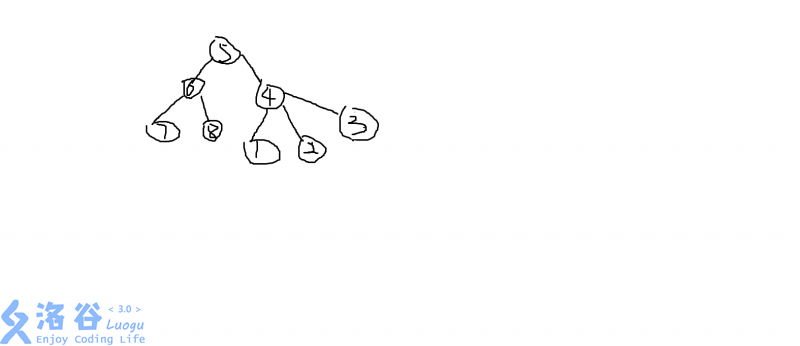
以4为根时： 观察发现:4的子树(包括自己)深度都减少了1,原根5的子树的深度都增加了1。

也就是说:对于x,它的父亲是y。

f[x]=f[y]-size[x]+n-size[x].

也就是说只要求出一个点,我们就可以用它求出其他点的ans。

这个方法叫二次扫描与换根法。

注:记得开long long

code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
struct edge
{
	int to,nxt;
}e[maxn<<1];
int n,cnt,id;
int head[maxn];
long long ans;
long long f[maxn],dep[maxn],size[maxn];
inline void add(int u,int v)
{
	e[++cnt].nxt=head[u];
	head[u]=cnt;
	e[cnt].to=v;
}
void dfs1(int x,int fa)
{
	size[x]=1;dep[x]=dep[fa]+1;
	for(int i=head[x];i;i=e[i].nxt)
	{
		int y=e[i].to;
		if(y==fa) continue;
		dfs1(y,x);
		size[x]+=size[y];
	}
}
void dfs2(int x,int fa)
{
	for(int i=head[x];i;i=e[i].nxt)
	{
		int y=e[i].to;
		if(y==fa) continue;
		f[y]=f[x]+n-2*size[y];
		dfs2(y,x);
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		int u,v;scanf("%d%d",&u,&v);
		add(u,v),add(v,u);
	}
	dfs1(1,0);
	for(int i=1;i<=n;i++) f[1]+=dep[i];
	dfs2(1,0);
	for(int i=1;i<=n;i++) if(ans<f[i]) ans=f[i],id=i;
	printf("%d",id);
	return 0;
}