自动搬运

查看原文

来自洛谷，原作者为

	kkksx AFO

搬运于2025-08-24 21:49:16，当前版本为作者最后更新于2019-02-04 14:31:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

搞不懂为啥要用并查集

思路:

从任一点出发遍历整个联通块，把走的点和边构成一棵树，当出现返祖边（即遍历过的点再一次被遍历），就把这一点以及它所有祖先所连的有向边全部反向，当然有可能点不在同一联通块内，那么直接枚举每一个点看有没有遍历过就行了

如图（表示不会画图）

正常遍历ing

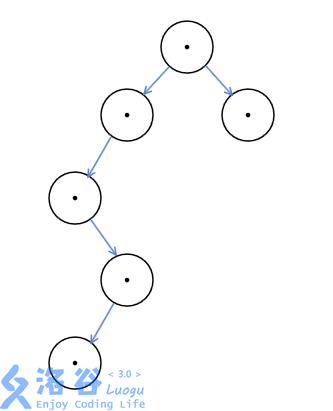
返祖

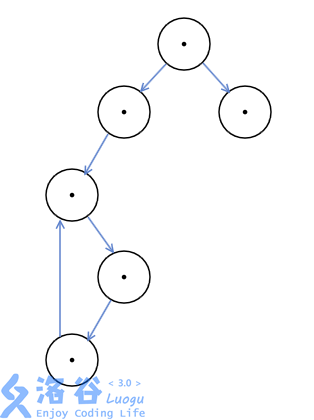
反向

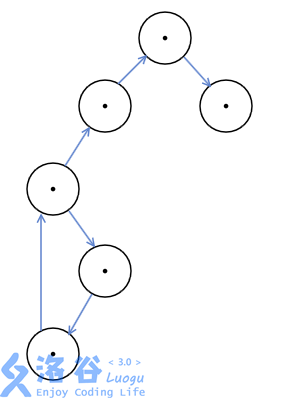
这样就满足每个点都有入度了

容易知道一棵树只需要一条返祖边就可以使得整个联通块有解，之后再出现返祖边直接不管。

无解：如果没有返祖边，那么整个联通块形成树结构，这棵树的根节点没有入度，就判无解。

巨丑代码如下（感觉很多地方可以省略~~，但谁叫我懒呢233~~）

#include<bits/stdc++.h> 
#define N 100001
#define M 200001
#define orz
using namespace std;
int n,m;
int ans[N],father[N];
bool vis[N],fanzu,ok=1;

struct Edge
{
	int next,to;
}edge[M*2]; int head[N],cnt;
void add_edge(int from,int to)
{
	edge[++cnt].next=head[from];
	edge[cnt].to=to;
	head[from]=cnt;
}

template <class T>
void read(T &x)
{
	char c;int sign=1;
	while((c=getchar())>'9'||c<'0') if(c=='-') sign=-1; x=c-48;
	while((c=getchar())>='0'&&c<='9') x=(x<<1)+(x<<3)+c-48; x*=sign;
}

void dfs2(int rt,int son)
{
	if(ans[rt]) dfs2(ans[rt],rt);//一直跳到根
	ans[rt]=son;
}

void dfs1(int rt)
{
	vis[rt]=1;
	for(int i=head[rt];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==father[rt]) continue;//回头 
		if(vis[v])//返祖 
		{
			if(!fanzu)//当前联通块未返祖，否则不管这条边 
			{
				fanzu=1;
				dfs2(v,rt);//回头更新 
			}
		}
		else//树边 
		{
			ans[v]=father[v]=rt;
			dfs1(v);
		}
	}
}

int main()
{
	read(n);read(m);
	for(int i=1;i<=m;++i)
	{
		int x,y;
		read(x);read(y);
		add_edge(x,y);
		add_edge(y,x);
	}
	for(int i=1;i<=n;++i)
	{
		if(!vis[i])//未走过 
		{
			fanzu=0;
			dfs1(i);
			if(!fanzu) {printf("NIE\n"); return 0;} 
		}
	}
	printf("TAK\n");
	for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
	return orz;
}