自动搬运

查看原文

来自洛谷，原作者为

	pythoner713 Hope deferred maketh the something sick.

搬运于2025-08-24 21:49:09，当前版本为作者最后更新于2021-10-22 13:56:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

按顺序，交替地，记录下多边形的边角信息。

例如样例中的第二个多边形：

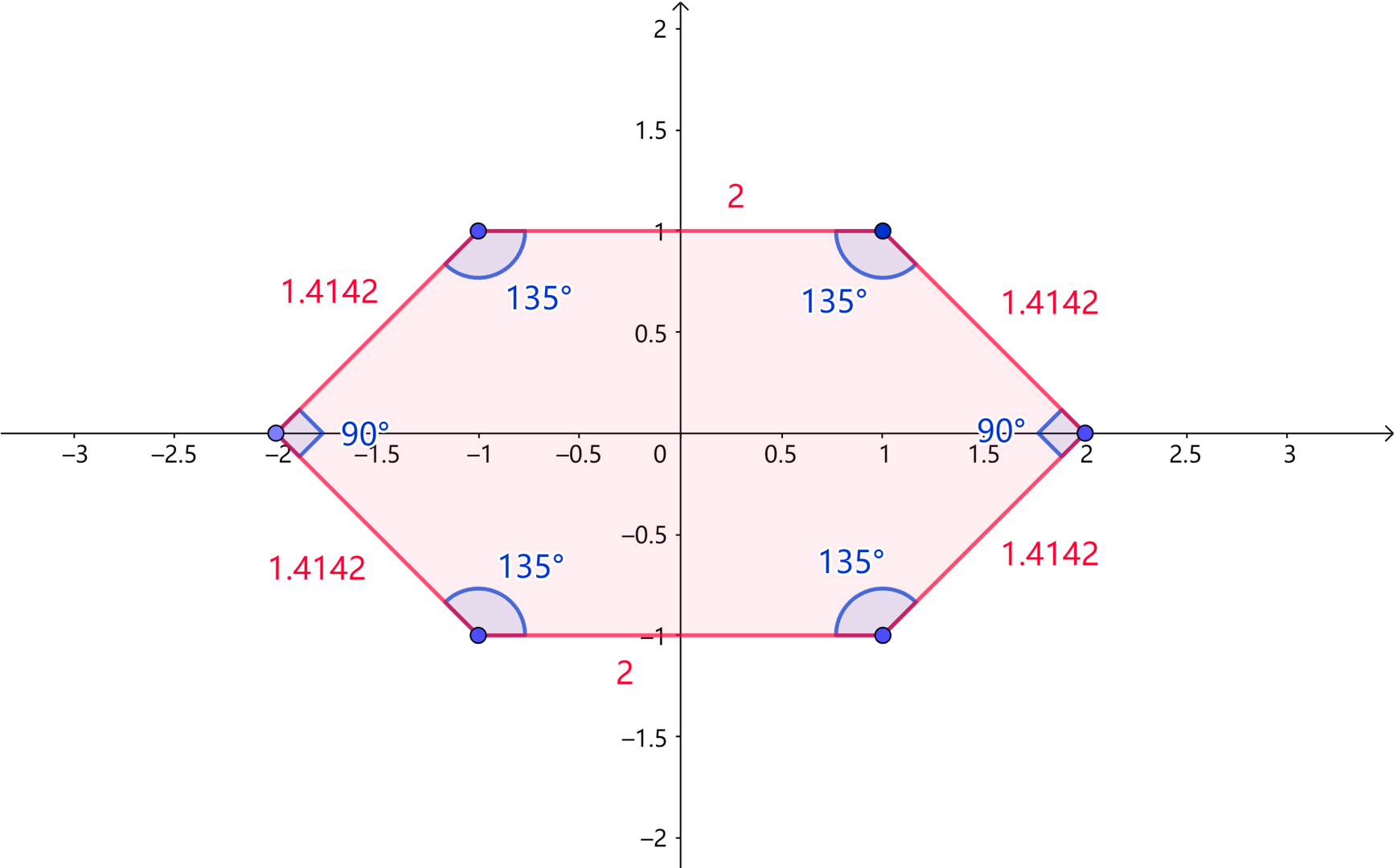
以右下角为起点，逆时针交替记录边角，得到长度为 $2n$ 的序列：

$$\sqrt2\to90\degree\to\sqrt2\to135\degree\to2\to135\degree\to\sqrt2\to90\degree\to\sqrt2\to135\degree\to2\to135\degree $$

这里的序列可以看作一个环，最后一项连向第一项。

角度与边长都是实数，不好处理。不如使用两条边向量的叉积代替角度，用边长的平方代替边长，这样就以将实数环转化为整数环：

$$2\to\underline2\to2\to2\to\underline4\to2\to2\to\underline2\to2\to2\to\underline4\to2 $$

此时，原多边形有几条对称轴即可转化为下列问题：环上有几个位置，满足将环从这里断开后，可以得到一条回文链？

在这个样例中，共有 $4$ 个位置满足条件，因此多边形有 $2$ 个对称轴（一条对称轴穿过两个位置）。

现在，我们把一个计算几何问题转化成了字符串问题。而本题解的创新之处在于返璞归真地用哈希解决了问题：我们将原长为 $2n$ 的序列倍长为 $4n$，然后对于每个 $1\le i\le 2n$，检查区间 $[i,i+2n]$ 是否为回文串（断环成链）。回文串的检查可以用哈希优化至 $\mathcal O(1)$，也就是对于原串正反分别做一次哈希，然后判断该区间的正反哈希值是否相等即可。

---

#include<bits/stdc++.h>
#define nb 400010
#define int long long
using namespace std;

int _, n, s[nb];
unsigned int B = 131, H1[nb], H2[nb], P[nb] = {1};
struct point{int x, y;}p[nb];

bool check(int l, int r){
	unsigned int h1 = H1[r] - H1[l - 1] * P[r - l + 1];
	unsigned int h2 = H2[l] - H2[r + 1] * P[r - l + 1];
	return h1 == h2;	// 正反哈希值相等说明回文
}

signed main(){
	for(int i = 1; i < nb; i++)
		P[i] = P[i - 1] * B;
	for(cin >> _; _--;){
		cin >> n;
		int ans = 0;
		for(int i = 1; i <= n; i++)
			cin >> p[i].x >> p[i].y;
		for(int i = 1; i <= n; i++){
			int A = i, B = i + 1, C = i + 2;
			B -= (B > n) * n, C -= (C > n) * n;
			s[i * 2 - 1] = pow(p[A].x - p[B].x, 2) + pow(p[A].y - p[B].y, 2);
			s[i * 2] = (p[A].x - p[B].x) * (p[B].y - p[C].y) - (p[A].y - p[B].y) * (p[B].x - p[C].x);
			// s[2i - 1] 和 s[2i] 分别记录边角信息
			// 叉积公式: (a, b) × (c, d) = ad - bc
		}
		for(int i = 1; i <= n * 2; i++) s[i + n * 2] = s[i];		  // 断环成链
		for(int i = 1; i <= n * 4; i++) H1[i] = H1[i - 1] * B + s[i]; // 正向哈希
		for(int i = n * 4; i >= 1; i--) H2[i] = H2[i + 1] * B + s[i]; // 反向哈希
		for(int i = 1; i <= n * 2; i++) ans += check(i, i + n * 2);	  // 判断回文
		cout << ans / 2 << endl;									  // 答案除二
	}
	return 0;
}