自动搬运

查看原文

来自洛谷，原作者为

	Hope2075 时间的流沙，淹没梦境里的夏

搬运于2025-08-24 21:48:56，当前版本为作者最后更新于2019-03-30 16:55:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

这题成为我人生第一道灰题（可能很快就不是了）

先平移坐标系，把起点移到原点，方便讨论

首先看看什么样的路线是合法的

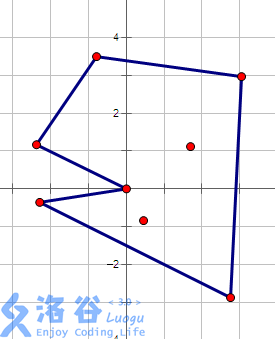
似乎有点什么特点

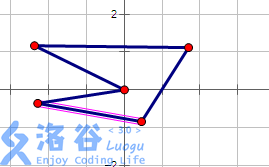
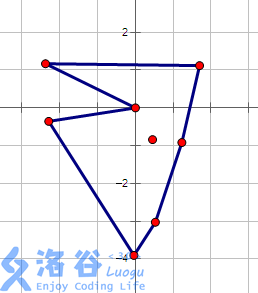
瞎猜一个结论：除了起点和终点外，，其它部分只要突出就可以

而且可以得到结论：最多转一圈

否则，当回来的时候，会发现起点已经被完全包围了

如果想绕进去，则会把自己困住

所以合法路径的特点：除了起点外，其它角度正确，且只绕一圈

考虑把点按极角排序，2号点极角为0，其它为从2号点顺时针旋转的角度

DP的时候，可以简单地认为从2号点出发，只能向顺时针方向前进

先考虑状态

如果只记录每个点，则不能判断能否继续走

如果再记录从哪个点来？

直接记录是$O(n^2)$状态

转移时，需要枚举所有可能的点对

这样是$O(n^3)$的，还有较多的计算，可能会超时

考虑一下性质：对每个点，将所有能到达它的点恰当地排序，可以满足接下来可以走的点数单调减少

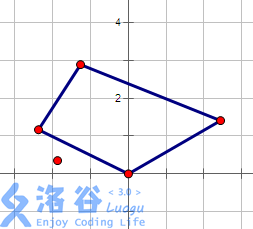
如果不理解，可以看看这个图

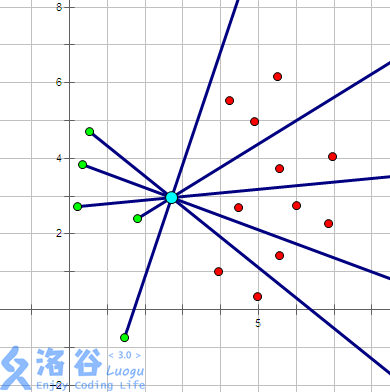
如果恰当地排序，则当选出的绿色点向下移动时，可以选的红色点向上减少

反过来也一样：选出的红色点向下移动时，可以选的绿色点会向上减少

可以想到单调队列或类似做法

但是这样会比较复杂

所以我就换了一个思路：记录当前点答案不小于$k$时，使得可选点范围最大的源点

这样可以发现DP值满足类似的性质，也就是：可以二分

转移时，枚举之前的点，二分最优答案，判断是否合法即可

另外，因为可能存在答案更差而且可选范围减小的结果，所以每完成一个点，从后向前扫一遍，把不优的DP值改成更优的就行

具体实现

为了防止精度问题，全文用int和叉积

按极角排序：

我的比较函数：先判断是否在基准线两侧

如果是，则可以直接得到结果

否则，两个点的极角差不会大于180度，可以用叉积判断

转移

枚举时判合法，只要这两个点相对位置正确就可以（用叉积判）

二分时，需要判断两条线段间夹角是否合法，也是用的叉积

二分完了要注意：如果一定不合法，要忽略这个答案

这种情况下，左下角那一个没有连上线段的点不会有DP值，也就不会更新后面的点

不然就可以开心地WA了

代码：

这里有些区别，请自行理解

包含输出方案功能部分，把if(0)改成if(1)就行

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1024;
struct vec{
	int x,y;
};
vec operator+(vec a,vec b){
	return (vec){a.x+b.x,a.y+b.y};
}
vec operator-(vec a,vec b){
	return (vec){a.x-b.x,a.y-b.y};
}
int operator*(vec a,vec b){
	return a.x*b.y-a.y*b.x;
}
vec base;
inline int sgn(int num){
	if(num>0)return 1;
	else if(num<0) return -1;
	else return 0;
}
bool operator<(vec a,vec b){
	if(sgn(a*base)*sgn(b*base)==-1){
		return a*base>0;
	}else{
		return a*b<0;
	}
}
int n;
vec list[N];
int dp[N][N];
vec F,P,C;
int l,r,mid;
int road[N],cnt;
int maxn,maxid;
int main(){
	ios::sync_with_stdio(false);
	cin>>n;
	cin>>list[n].x>>list[n].y;
	for(int i=1;i<n;i++){
		cin>>list[i].x>>list[i].y;
		list[i]=list[i]-list[n];
	}
	list[n].x=list[n].y=0;
	base=list[1];
	sort(list+2,list+n);
	dp[1][0]=dp[1][1]=n;
	for(int i=2;i<=n;i++){
		C=list[i];
		for(int j=1;j<i;j++){
			P=list[j];
			if(P*C>0)continue;
			l=0,r=n+1;
			while(l!=r){
				mid=((l+r)>>1);
				if(dp[j][mid]==0){
					r=mid;
					continue;
				}
				F=list[dp[j][mid]];
				if((P-F)*(C-P)<=0){
					l=mid+1;
					continue;
				}else{
					r=mid;
				}
			}
			if(dp[j][l-1]==0)continue;
			//这里一定要判，否则会产生不合法转移
			if(maxn<l){
				maxn=l;
				maxid=i;
			}
			if(dp[i][l]==0){
				dp[i][l]=j;
			}else{
				F=list[dp[i][l]];
				if((C-P)*(C-F)<0){
					dp[i][l]=j;
				}
			}
		}
		for(int j=n;j>=0;j--){
			if(dp[i][j]==0)dp[i][j]=dp[i][j+1];
			else{
				if(dp[i][j+1]==0)continue;
				F=list[dp[i][j]];
				P=list[dp[i][j+1]];
				if((C-P)*(C-F)<0){
					dp[i][j]=dp[i][j+1];
				}
			}
		}
	}
	cout<<maxn-1<<endl;
	road[cnt++]=n;
	for(int p=dp[n][maxn],t=maxn;p!=n;--t,p=dp[p][t]){
		road[cnt++]=p;
	}
	if(0){
		for(int i=cnt-1;i>=0;i--){
			cout<<road[i]<<" ";
		}
	}
}