1 条题解

  • 0
    @ 2025-8-24 21:48:54

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar agicy
    你很懒，什么都看不到

    搬运于2025-08-24 21:48:54，当前版本为作者最后更新于2021-06-10 22:21:57，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    本文将同步发布于：

    题目

    题目链接：洛谷 P3428、官网。

    题意简述

    给定 nn 个圆 (xi,yi,ri)(x_i,y_i,r_i)，每个圆对应一个点集 $S_i=\left\{(x,y)\mid (x-x_i)^2+(y-y_i)^2\leq r_i^2\right\}$。

    求一个最小的 ii 满足 ∩j=1iSj=∅\cap_{j=1}^i S_j=\varnothing；如果无解输出 NIE。

    题解

    简单又自然的随机化

    我们考虑枚举 ii，然后判定 S1∼iS_{1\sim i} 的交集是否为空。

    如何判定呢？我们想到一个简单的方法，我们随机一些在圆的边界上的点，只需要判定这些点是否存至少在一个点在所有圆内即可。

    这种方法简单又自然，但是随机化算法正确率不高，这远远不够。

    研究几何性质

    如果做计算几何题而抛弃几何性质，所得到的做法往往是劣解。

    继续沿着上面的思路，我们同样考虑枚举 ii，然后判定 S1∼iS_{1\sim i} 的交集是否为空。

    不同的是，我们定义一个交集中横坐标最大的点为代表点（代表点只会有一个，这是因为圆是凸集，凸集的交集还是凸集）。

    我们发现，如果一些圆的交集非空，那么其代表点一定满足：它是所有圆两两交集的代表中横坐标最小的那个。

    证明十分显然，考虑交集的意义即可。

    最后的结论

    综上所述，对于一个 ii，我们只需要求出 1∼i−11\sim i-1 与 ii 的代表点即可，如果所有代表点中横坐标最小的那一个在所有的圆内，那么其合法，否则不合法，换言之，答案为 ii。

    我们考虑证明这个结论：

    • 若没有交集，则这个点必然不合法，符合我们的预期；
    • 若有交集，则我们需要证明这个点是交集的代表点。
      • 假设其不是交集的代表点，则交集的代表点可能在其左右；
      • 左边：不可能，若交集存在，则代表点的横坐标 ≥\geq 当前点横坐标。
      • 右边：不可能，考虑当前点在 Sa∩SbS_a\cap S_b 中得到，那么所有 x≥x\geq 当前点横坐标的点均被交集抛弃，因此代表点的横坐标 ≤\leq 当前点横坐标。
      • 由夹逼过程可知结论正确。

    这个算法的时间复杂度为 Θ(n2)\Theta(n^2)。

    参考程序

    下面我们来解决两圆求交的问题。

    下面介绍一下两种方法：余弦定理和相似三角形。

    余弦定理

    用余弦定理求解需要用到三角函数，常数大，精度差。

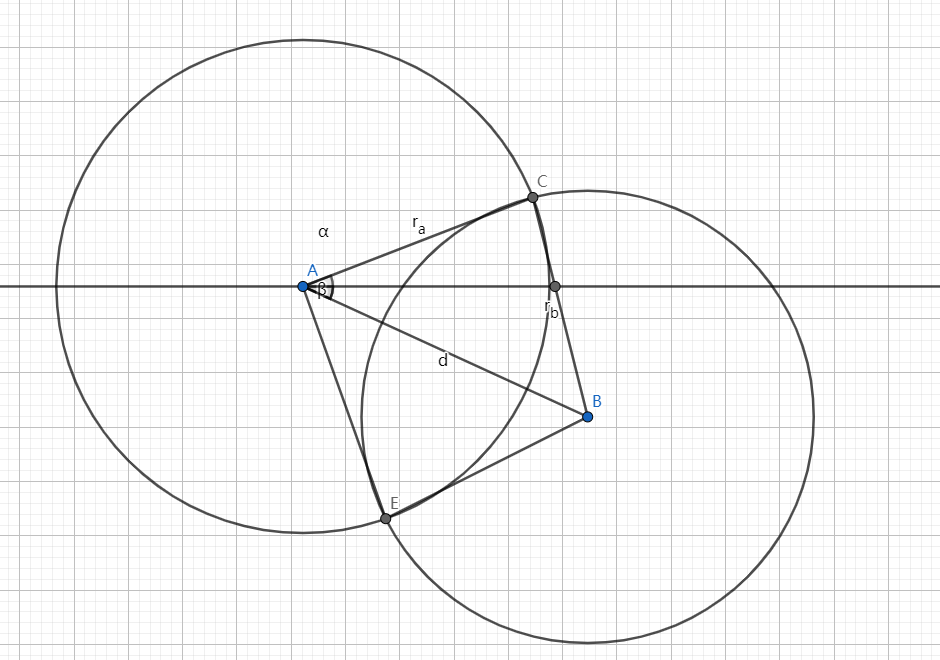
    我们考虑下图：

    2WRtN4.png

    对 △ACB\triangle{ACB} 运用余弦定理，得到 ra2+d2−2dracos⁡α=rb2r_a^2+d^2-2dr_a\cos\alpha=r_b^2，进而求出 $\alpha=\arccos\left(\frac{r_a^2+d^2-r_b2}{2dr_a}\right)$。

    然后我们再求出基准角 β\beta，显然 β=atan2(yb−ya,xb−xa)\beta=\texttt{atan2}(y_b-y_a,x_b-x_a)。

    因此，我们得到了 C,DC,D 两点的对 AA 的极角为 β+α\beta+\alpha，β−α\beta-\alpha。

    对于极角为 θ\theta，极径为 rar_a 的点，我们得出其对应点的坐标为 (racos⁡θ,rasin⁡θ)(r_a\cos\theta,r_a\sin\theta)。

    #include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;

const double eps=1e-6;

inline int sgn(reg double x){
	if(fabs(x)<eps)
		return 0;
	else
		return x<0?-1:1;
}

inline double sqr(reg double x){
	return x*x;
}

const int MAXN=2e3+5;

struct Vector{
	double x,y;
	inline Vector(reg double x=0,reg double y=0):x(x),y(y){
		return;
	}
	inline Vector operator+(const Vector& a)const{
		return Vector(x+a.x,y+a.y);
	}
	inline Vector operator-(const Vector& a)const{
		return Vector(x-a.x,y-a.y);
	}
	inline Vector operator*(const double a)const{
		return Vector(x*a,y*a);
	}
};

inline double dot(const Vector& a,const Vector& b){
	return a.x*b.x+a.y*b.y;
}

inline double cross(const Vector& a,const Vector& b){
	return a.x*b.y-a.y*b.x;
}

typedef Vector Point;

inline double getDis2(const Point& a,const Point& b){
	return dot(a-b,a-b);
}

inline double getDis(const Point& a,const Point& b){
	return sqrt(getDis2(a,b));
}

inline bool isEmpty(const Point& a){
	return a.x!=a.x||a.y!=a.y;
}

struct Circle{
	Point o;
	double r;
	inline bool contain(const Point& x)const{
		return sgn(sqr(r)-getDis2(x,o))>=0;
	}
	inline Point getRig(void)const{
		return o+Vector(r,0);
	}
};

inline bool isCon(const Circle& a,const Circle& b){
	return sgn(sqr(a.r-b.r)-getDis2(a.o,b.o))>=0;
}

inline bool isSep(const Circle& a,const Circle& b){
	return sgn(getDis2(a.o,b.o)-sqr(a.r+b.r))>0;
}

inline Point getPot(const Circle &a,const Circle &b){
	if(isCon(a,b))
		if(sgn(b.getRig().x-a.getRig().x)>0)
			return a.getRig();
		else
			return b.getRig();
	else if(isSep(a,b))
		return Point(nan(""),nan(""));
	else{
		if(a.contain(b.getRig()))
			return b.getRig();
		else if(b.contain(a.getRig()))
			return a.getRig();
		else{
			reg double d=getDis(a.o,b.o);
			reg double ang=acos(((sqr(a.r)+sqr(d))-sqr(b.r))/(2*a.r*d));
			reg double delta=atan2(b.o.y-a.o.y,b.o.x-a.o.x);
			reg double ang1=delta+ang,ang2=delta-ang;
			Point p1=a.o+Vector(cos(ang1)*a.r,sin(ang1)*a.r);
			Point p2=a.o+Vector(cos(ang2)*a.r,sin(ang2)*a.r);
			Point res;
			if(sgn(p2.x-p1.x)>0)
				res=p2;
			else
				res=p1;
			return res;
		}
	}
}

int n;
Circle a[MAXN];

int main(void){
	scanf("%d",&n);
	Point lef(0,0);
	for(reg int i=1;i<=n;++i){
		static int x,y,r;
		scanf("%d%d%d",&x,&y,&r);
		a[i].o=Point(x,y),a[i].r=r;
		if(i==2)
			lef=getPot(a[1],a[2]);
		else if(i>2){
			for(reg int j=1;j<i&&!isEmpty(lef);++j){
				Point tmp=getPot(a[i],a[j]);
				if(isEmpty(tmp)||tmp.x<=lef.x)
					lef=tmp;
			}
			for(reg int j=1;j<=i&&!isEmpty(lef);++j)
				if(!a[j].contain(lef))
					lef=Point(nan(""),nan(""));
		}
		if(isEmpty(lef)){
			printf("%d\n",i);
			return 0;
		}
	}
	puts("NIE");
	return 0;
}

    相似三角形

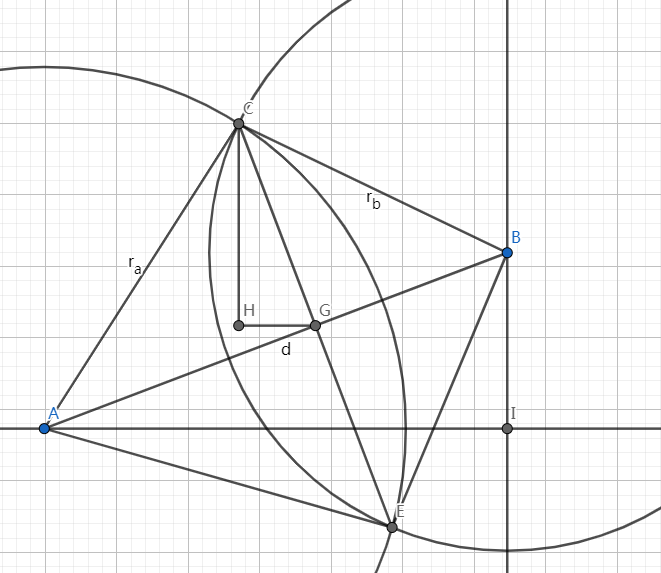
    2WRN4J.png

    如上图，我们设 a=∣AG∣a=|AG|，b=∣BG∣b=|BG|，h=∣CG∣h=|CG|。

    那么我们有：

    $$\begin{cases}r_a^2=a^2+h^2\\r_b^2=b^2+h^2\\a+b=d\end{cases} $$

    那么我们有：

    a=ra2+d2−rb22da=\frac{r_a^2+d^2-r_b^2}{2d}

    然后考虑 △AIB∼△CHG\triangle AIB\sim\triangle CHG，我们有：

    (yb−ya)h=d(yc−yg)(y_b-y_a)h=d(y_c-y_g)

    我们可由此解出坐标，其他同理可算出。

    #include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;

const double eps=1e-6;

inline int sgn(reg double x){
	if(fabs(x)<eps)
		return 0;
	else
		return x<0?-1:1;
}

inline double sqr(reg double x){
	return x*x;
}

const int MAXN=2e3+5;

struct Vector{
	double x,y;
	inline Vector(reg double x=0,reg double y=0):x(x),y(y){
		return;
	}
	inline Vector operator+(const Vector& a)const{
		return Vector(x+a.x,y+a.y);
	}
	inline Vector operator-(const Vector& a)const{
		return Vector(x-a.x,y-a.y);
	}
	inline Vector operator*(const double a)const{
		return Vector(x*a,y*a);
	}
};

inline double dot(const Vector& a,const Vector& b){
	return a.x*b.x+a.y*b.y;
}

inline double cross(const Vector& a,const Vector& b){
	return a.x*b.y-a.y*b.x;
}

typedef Vector Point;

inline double getDis2(const Point& a,const Point& b){
	return dot(a-b,a-b);
}

inline double getDis(const Point& a,const Point& b){
	return sqrt(getDis2(a,b));
}

inline bool isEmpty(const Point& a){
	return isnan(a.x)||isnan(a.y);
}

struct Circle{
	Point o;
	double r;
	inline bool contain(const Point& x)const{
		return sgn(sqr(r)-getDis2(x,o))>=0;
	}
	inline Point getRig(void)const{
		return o+Vector(r,0);
	}
};

inline bool isCon(const Circle& a,const Circle& b){
	return sgn(sqr(a.r-b.r)-getDis2(a.o,b.o))>=0;
}

inline bool isSep(const Circle& a,const Circle& b){
	return sgn(getDis2(a.o,b.o)-sqr(a.r+b.r))>0;
}

inline Point getPot(const Circle &a,const Circle &b){
	if(isCon(a,b))
		if(sgn(b.getRig().x-a.getRig().x)>0)
			return a.getRig();
		else
			return b.getRig();
	else if(isSep(a,b))
		return Point(nan(""),nan(""));
	else{
		if(a.contain(b.getRig()))
			return b.getRig();
		else if(b.contain(a.getRig()))
			return a.getRig();
		else{
			reg double d=getDis(a.o,b.o);
			reg double val=(sqr(a.r)+sqr(d)-sqr(b.r))/(2*d);
			reg double h=sqrt(sqr(a.r)-sqr(val));
			Point bas=a.o+(b.o-a.o)*(val/d);
			Vector tmp=Vector(b.o.y-a.o.y,a.o.x-b.o.x)*(h/d);
			Point p1=bas-tmp,p2=bas+tmp;
			if(sgn(p2.x-p1.x)>0)
				return p2;
			else
				return p1;
		}
	}
}

int n;
Circle a[MAXN];

int main(void){
	scanf("%d",&n);
	Point lef(0,0);
	for(reg int i=1;i<=n;++i){
		static int x,y,r;
		scanf("%d%d%d",&x,&y,&r);
		a[i].o=Point(x,y),a[i].r=r;
		if(i==2)
			lef=getPot(a[1],a[2]);
		else if(i>2){
			for(reg int j=1;j<i&&!isEmpty(lef);++j){
				Point tmp=getPot(a[i],a[j]);
				if(isEmpty(tmp)||tmp.x<=lef.x)
					lef=tmp;
			}
			for(reg int j=1;j<=i&&!isEmpty(lef);++j)
				if(!a[j].contain(lef))
					lef=Point(nan(""),nan(""));
		}
		if(isEmpty(lef)){
			printf("%d\n",i);
			return 0;
		}
	}
	puts("NIE");
	return 0;
}
    • 1

    [POI 2005] AKC-Special Forces Manoeuvres

    信息

    ID
    2505
    时间
    1000ms
    内存
    128MiB
    难度
    6
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 24ms