自动搬运

查看原文

来自洛谷，原作者为

	Salty_Fish787 **

搬运于2025-08-24 21:48:46，当前版本为作者最后更新于2019-08-20 19:39:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

$Solution:$

• 题意： 求

$$\sum_{i\in[0,n],2|i}C_n^i$$

的值。答案对$6662333$取模，且$n\leq 10^{18}$。

• 前置芝士：二项式定理

$$(a+b)^n=\sum_{i=0}^n C_n^ia^ib^{n-i}$$

将$a=1,b=1$代入：

$$(1+1)^n=2^n=\sum_{i=0}^n C_n^i$$

即

$$C_n^0+C_n^1+C_n^2+...+C_n^n=2^n(1)$$

将$a=1,b=-1$代入：

$$(1-1)^n=0=\sum_{i=0}^n (-1)^iC_n^i$$

即

$$C_n^0-C_n^1+C_n^2+...+(-1)^nC_n^n=0(2)$$

• 分析：由$(1)$式$+(2)$式除以$2$得：

$$C_n^0+C_n^2+C_n^4+...+C_n^{[\frac{n}{2}]\times 2}=\frac{2^n+0}{2}=2^{n-1} $$

其中$[x]$表示$x$的整数部分。当$x$为奇数时，$[\frac{x}{2}]\times 2=x-1$；当$x$为偶数时，$[\frac{x}{2}]\times 2=x$。 即

$$\sum_{i\in[0,n],2|i}C_n^i=2^{n-1}$$

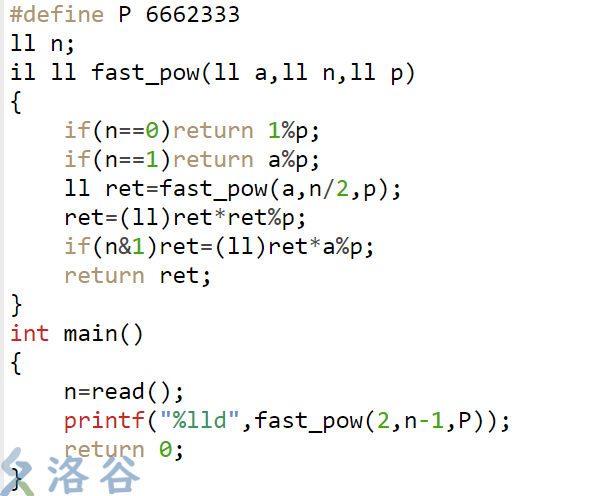
综上所述，直接输出$2^{n-1}mod6662333$的值即可。用快速幂维护。

• $code:$