自动搬运

查看原文

来自洛谷，原作者为

	Rachel_in **

搬运于2025-08-24 21:48:43，当前版本为作者最后更新于2019-05-29 11:12:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

介绍一下闭合图的概念，闭合图是建立在有向图上的，就是对于一个集合内每个点，它能达到的所有点都在这个集合里面。

对于样例：

输入
2 3
10 1 2 0
25 2 3 0
5 6 7

输出
17

我们构成的图为：

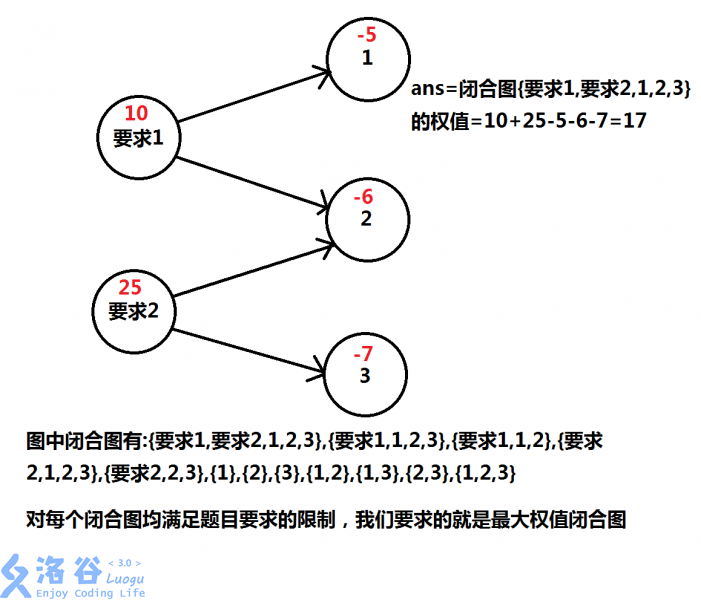
对于最大权值闭合图，我们需要用最小割来做。

我们重新构图：

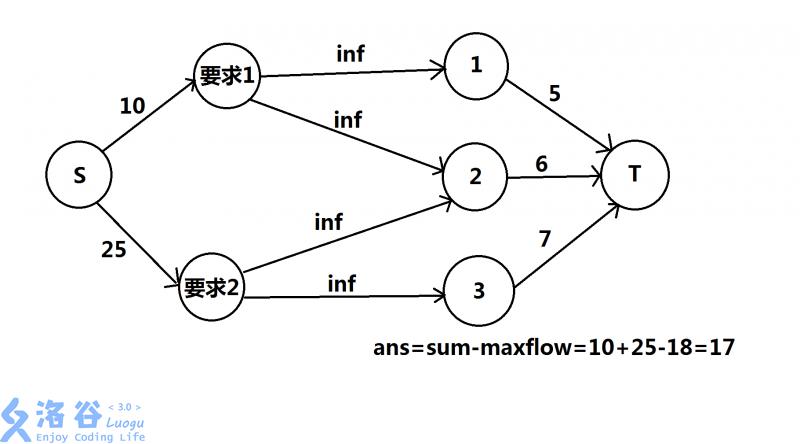
前置结论：最大权值=闭合图的正权值之和-最小割

理解边的含义：

我们做的最小割一定不会切到无穷大的边，所以割里的边都是$S->u$或者$u->T$。

对于割掉一个$S->u$的边含义为在闭合图中不选择$u$这个点,对于割掉一个$u->T$的边含义为在闭合图中选择$u$这个点。

(注意：这里边的含义很难去想它为什么要这么定义的时候，先看下去，之后会明白的)

举个例子：我们在网络流那张图里割去权值为10,5,7这些边，含义为不选择要求1，选择1,3这些点，也就是一共选择要求2,1,3这三个点，这不是一个闭合图，因为2这个点没选。然后我们发现网络流里有非0流的，不是割，也就是说如果选择的不是网络流的割，那么选到的点集必定不是闭合图。

证明：如果$S$与$T$连通，则存在点$u$,$v$，使得$S$到$u$有边，$u$到$v$连通，$v$到$T$有边，所以$v$一定是$u$的后继，但选择了$u$，没有选择$v$，不是闭合子图。

得出结论：只有$S$与$T$不连通时，才能得到闭合子图。

于是我们要求出的是割，至于要将答案最大化：

最小割=不选的$S$到$u$的边权和+选择的$u$到$S$的边权和

闭合图最大权值=全部正权点之和-不选的正权点之和+选择的负权点之和

加上选择的负权点之和就相当于减去选择的负权点的绝对值之和，也就是选择的$u$到$S$的边权和

所以:

闭合图最大权值=全部正权点之和-不选的$S$到$u$的边权和-选择的$u$到$S$的边权和

也就是：

闭合图最大权值=全部正权点之和-最小割

应该可以理解边的含义了吧

部分参考博客

代码：

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int res=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){res=(res<<3)+(res<<1)+ch-'0';ch=getchar();}	
	return res*f;
}
const int N=255;
const int M=40555;
const int inf=1e7;
int S,T,n,m,fir[N],cur[N],dep[N],nxt[M],go[M],val[M],cnt=1,maxflow,ans;
queue<int> Q;
inline void Add(int u,int v,int w){
	nxt[++cnt]=fir[u];
	fir[u]=cnt;
	go[cnt]=v;
	val[cnt]=w;
}
inline bool bfs(){
	for(int i=S;i<=T;i++) dep[i]=-1;
	dep[S]=0;
	Q.push(S);
	while(!Q.empty()){
		int u=Q.front();Q.pop();
		for(int e=fir[u];e;e=nxt[e]){
			int v=go[e];	
			if(dep[v]==-1&&val[e]>0){
				dep[v]=dep[u]+1;	
				Q.push(v);
			}			
		}		
	}
	if(dep[T]==-1) return 0;
	else return 1;
}
int dfs(int u,int flow){
	if(u==T) return flow;
	for(int &e=cur[u];e;e=nxt[e]){
		int v=go[e];	
		if(dep[v]==dep[u]+1&&val[e]>0){
			int f=dfs(v,min(flow,val[e]));
			if(f>0){
				val[e]-=f;val[e^1]+=f;	
				return f;
			}			
		}	
	}
	return 0;
}
void Dinic(){
	while(bfs()){
		for(int i=S;i<=T;i++) cur[i]=fir[i];		
		while(int d=dfs(S,inf)){
			maxflow+=d;
		}
	}
}
int main(){
	m=read();n=read();
	S=0;T=m+n+1;
	for(int i=1;i<=m;i++){
		int w=read();	
		ans+=w;
		Add(S,i,w);Add(i,S,0);
		int x=read();
		while(x){
			Add(i,m+x,inf);Add(m+x,i,0);
			x=read();
		}
	}	
	for(int i=1;i<=n;i++){
		int w=read();
		Add(m+i,T,w);Add(T,m+i,0);
	}
	Dinic();
	printf("%d",ans-maxflow);
	return 0;
}