自动搬运

查看原文

来自洛谷，原作者为

	Ofnoname 亡者归来

搬运于2025-08-24 21:48:36，当前版本为作者最后更新于2019-09-30 23:42:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

吾闻悬线法之名而来，却以单调栈为之。

十有九者闻单调队列而不闻单调栈，殊不知其外有不同，内为一体。

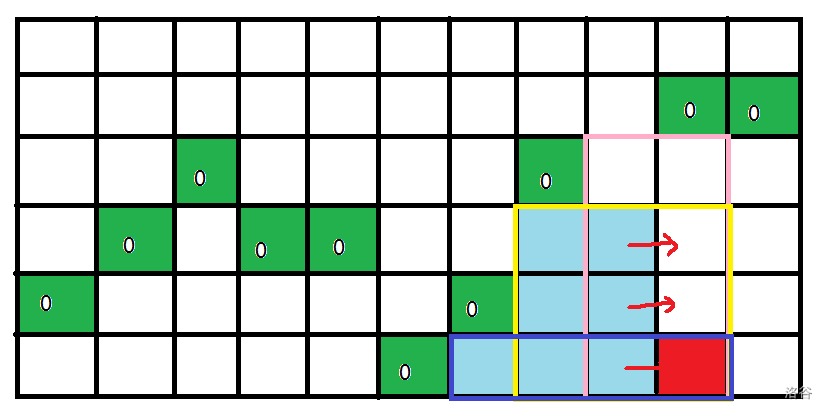
统计每一个点作为右下角时可以得到多少矩形，加起来就是答案。这里以图中的红点为例。

对于这个红点，这些各色矩形内的点就是可取的答案，矩形的大小因为0的存在受到限制。容易发现，这些挡住矩形的‘0’从左往右是单调递增的，而比这些0更靠左还更高的‘0’显然是毫无用处的。

所以我们可以维护一个栈，从左往右扫时，就把显然没有用的‘0’直接排除。

统计答案时，因为本列的0一定不低于左边一列的0，所以之前左边一列的答案（浅蓝色）可以直接继承，同时还要加上最新一个形成的矩形(粉色矩形上端)贡献的答案。

相邻两横行的每列0高度是无法推出来的，所以每一行要重新弄一个单调栈。

要开long long

#include <bits/stdc++.h>
#define u32 unsigned int
#define u64 unsigned long long
#define MAX (3000 + 7)
using namespace std;

u32 N,M,top,S[MAX],f[MAX],sum[MAX],a[MAX][MAX];
u64 ans;

int main()
{
	scanf("%u%u", &N, &M);
	for (u32 i = 1; i <= N; i++)
	for (u32 j = 1; j <= M; j++)
		scanf("%u", &a[i][j]);
	for (u32 i = 1; i <= N; i++, top = 0)//清空单调栈 
	for (u32 j = 1; j <= M; j++) 
	{
		if (!a[i][j]) f[j] = i;//统计本列最低的0. 
		while (top && f[S[top]]<f[j]) top--; S[++top] = j;//排除比我靠左还比我高的点 
		ans += (sum[top] = sum[top-1] + (i - f[S[top]]) * (S[top] - S[top-1]));
		//继承左列答案，加上新矩形的答案 
	} printf("%llu\n", ans);	
}

做完这个可以去做讨论里的两道双倍经验，数据范围比这个小多了