自动搬运

查看原文

来自洛谷，原作者为

	lemir3 月符「Silent Selene」

搬运于2025-08-24 21:48:26，当前版本为作者最后更新于2019-07-01 13:30:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

获得更好的阅读体验

#什么是二分图?

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。------摘自百度百科

#怎样判定二分图?

以下内容摘自《算法竞赛进阶指南》

存在如下定理:

一张无向图是二分图,当且仅当图中不存在奇环(长度为奇数的环).

根据该定理,同志们可以以染色法进行二分图的判定.主体思想为:尝试用黑白两种颜色标记图中的结点,当一个结点被标记后,它的所有相邻结点应该被标记与它相反的颜色.若标记过程中产生冲突,则说明图中存在奇环.二分图染色一般基于DFS实现,时间复杂度为$O(n+m)$,伪代码如下:

void dfs(int x,int color)
{
    赋值v[x] <-- color
    对于与x相连的每条无向边(x,y)
    if v[y]=0 then
        dfs(y,3-color)
    else if v[y]=color then
        判定无向图不是二分图,算法结束
}

在主函数中
    for i <-- 1 to n
        if(v[i]=0)then dfs(i,1)
    判定无向图是二分图

#二分图最大匹配

以下定义摘自《算法竞赛进阶指南》

"任意两条边没有公共端点"的边的集合被称为图的一组匹配.在二分图中,包含边数最多的一组匹配被称为二分图的最大匹配.

对于任意一组匹配$S$($S$是边集),属于$S$的边被称为"匹配边",不属于$S$的边被称为"非匹配边".匹配边的端点被称为"匹配点",其他结点被称为"匹配点".如果二分图中存在一条连接两个非匹配点的路径$path$,使得非匹配边与匹配边在$path$上交错出现,那么称$path$是匹配$S$的增广路,也称交错路.

有如下定理:

二分图的一组匹配$S$是最大匹配,当且仅当图中不存在$S$的增广路.

配图如下:

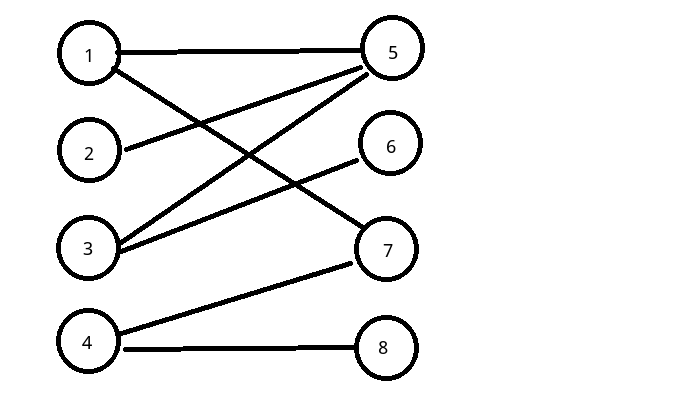
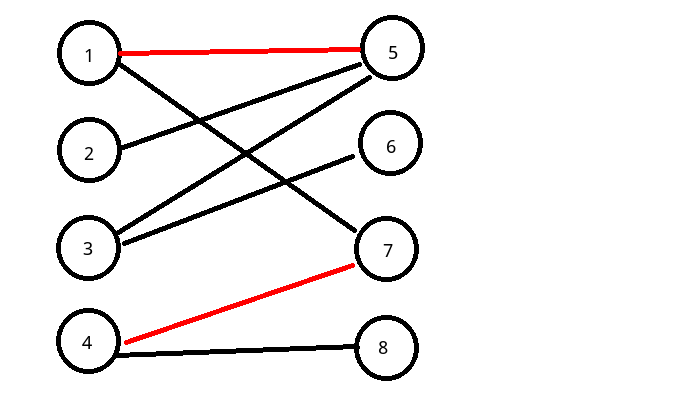
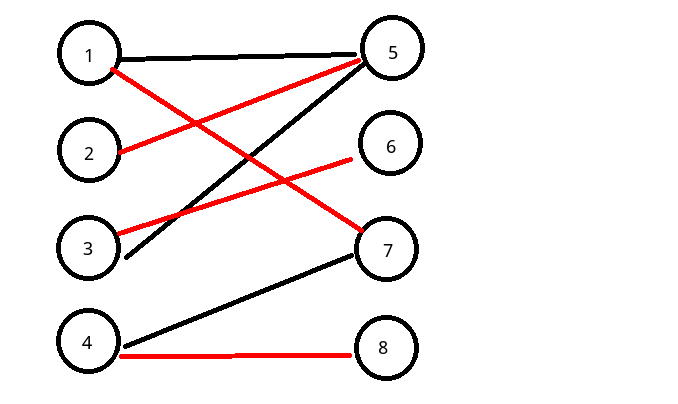
如图,图2,图3(请不要联想到图波耶夫设计局)中红色的边就是图1的匹配,图3中红色的边为图1的最大匹配.

##匈牙利算法(增广路算法)

匈牙利算法,又称增广路算法,用于计算二分图最大匹配.

###引入

独立团战士们要发枪,每个战士都有自己想要的枪.关系如下:

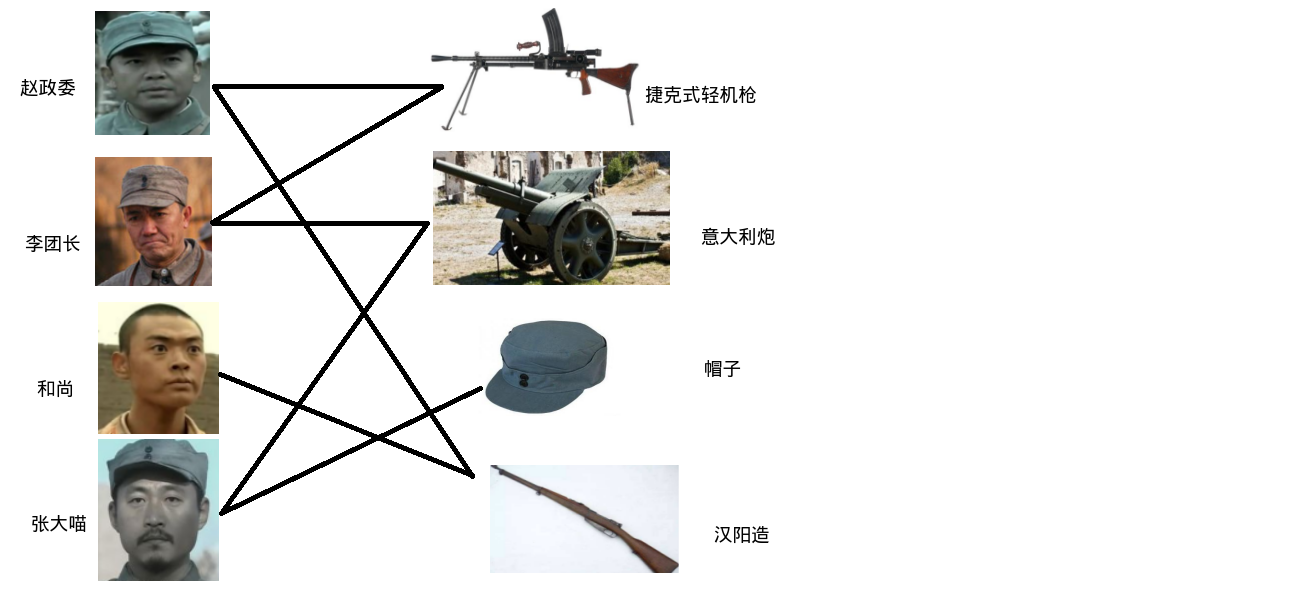
开始分配:

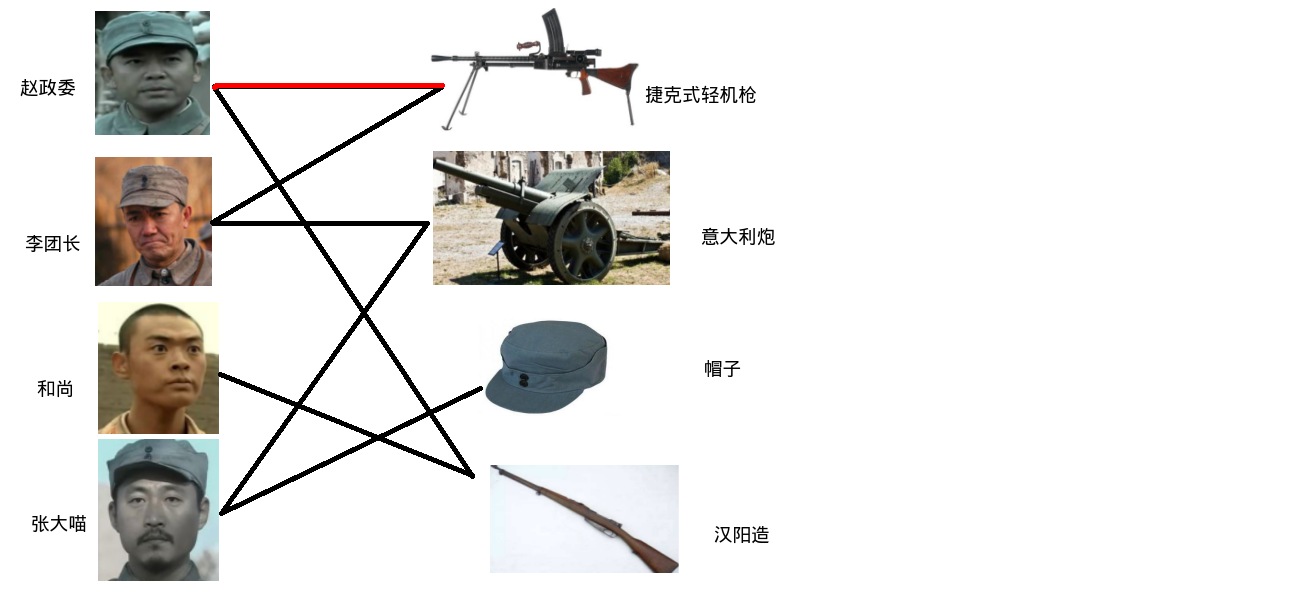
政委想要捷克式轻机枪,于是把捷克式轻机枪分给了政委.

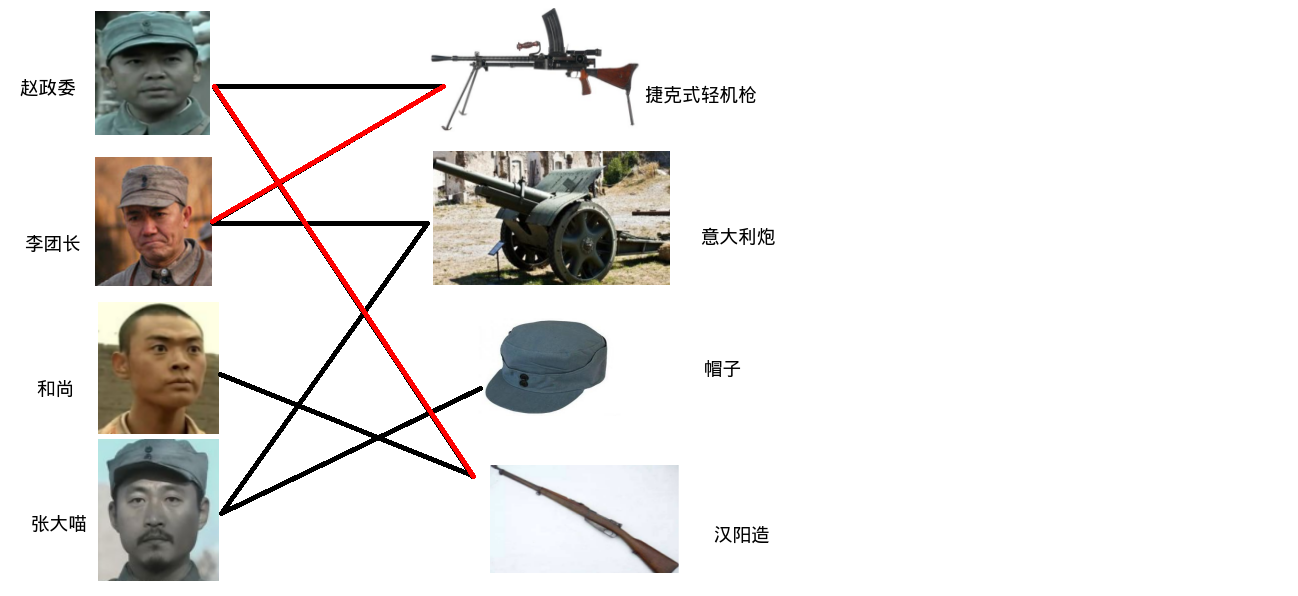
团长这时说道:"好你他娘的赵政委,当几天政委还蹭鼻子上脸了是吧?老子就要用捷克式轻机枪."

政委想了想,反正咱百里赵刚用汉阳造也顺手,顺手拿来了汉阳造,轻机枪给了团长.

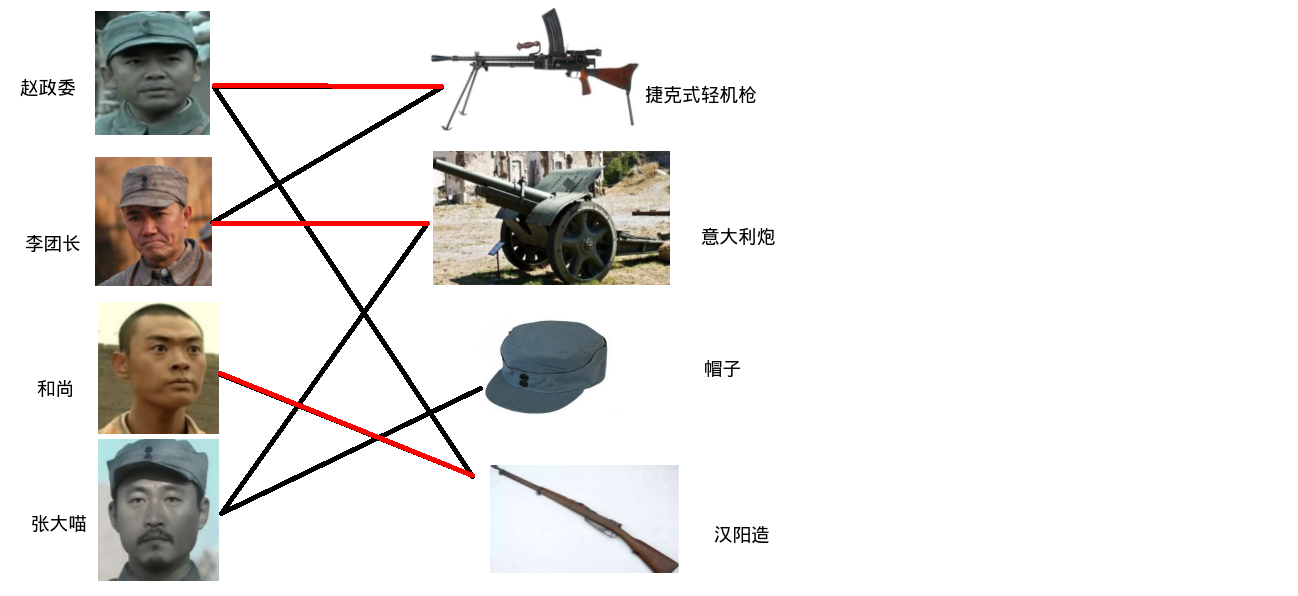
但是和尚也想用这把汉阳造,于是找政委商量.

政委:"关心小同志是咱当政委的职责,要不这样,这把汉阳造就拿给你用,我去找团长商量用轻机枪."

团长:"怎么?又打老子的轻机枪的主意?我看你和老子还有几天交情,轻机枪给你用,行了吧,读书人还真他娘的不讲理.这几天闲着没事,二营的那台意大利炮,老子拿来玩几天."

于是团长从二营拖来了意大利炮,政委用上了轻机枪,和尚拿到了汉阳造.

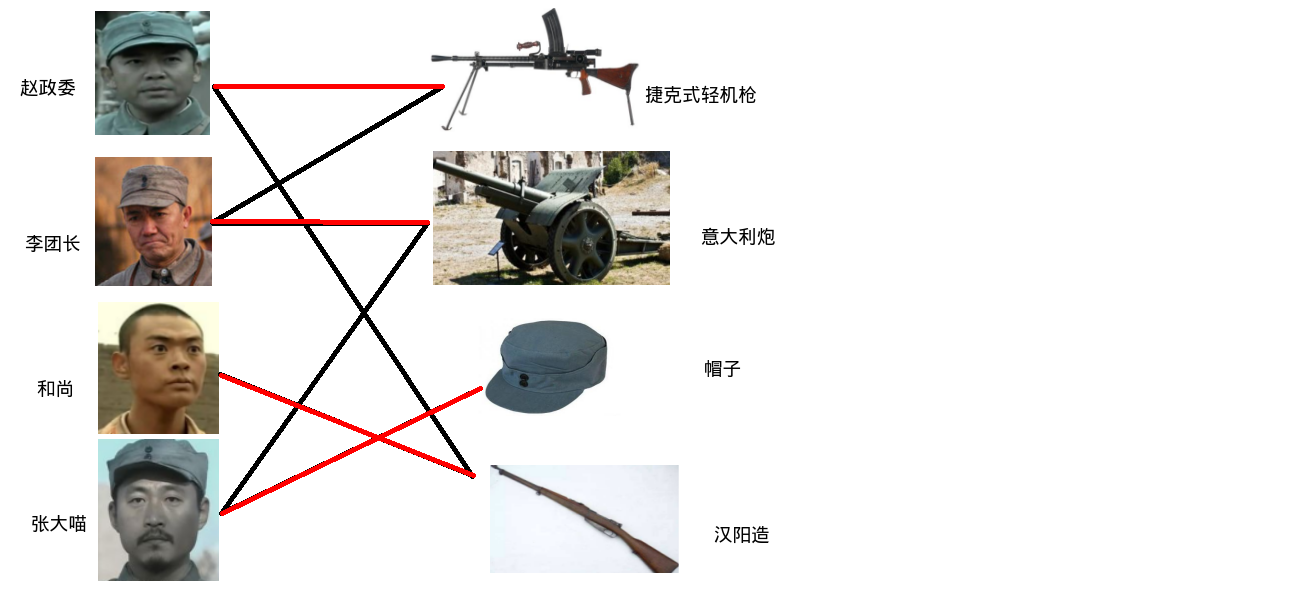
二营长这就不乐意了,我堂堂张大喵彪,好不容易缴获的意大利炮,哪是个团长随随便便就能拿来玩的?

于是张大喵彪找到了团长.

团长:"去你他娘的二营长,老子官比你大,用你的炮怎么啦?老子把炮给你了老子用什么打仗?你让那小鬼子自个往我嘴里钻?我看你打仗天天摔帽子,那顶上次去边区领多了一顶帽子,你给老子拿去用."

于是张大喵彪分到了一顶帽子.

###主体思想

上面的过程就是一个标准的匈牙利算法.

匈牙利算法的思想就是寻找增广路,把增广路上的匹配状态全部取反,得到一个更大的匹配.

具体来说的话,可以以上面的第二幅图举例.

"李团长 --> 捷克式轻机枪 --> 赵政委 --> 汉阳造",这是匹配"赵政委 --> 捷克式轻机枪"的一条增广路,其中"李团长"和"汉阳造"为增广路连接的两个非匹配点.同志们把这条增广路上的所有边的匹配状态取反,原来政委拿到了轻机枪,取反之后变为没有拿到,原来团长没有拿到轻机枪,取反后拿到了轻机枪,原来政委没有拿到汉阳造,取反后拿到了汉阳造.

这样就得到了一个更大的匹配.

我们重复第二步,直到图中不存在增广路,就得到了最大匹配.

因为该算法最多遍历整个二分图一次,所以时间复杂度为$O(nm)$.

###具体实现

1. 设$S$为空集,即所有的边都是非匹配边.

2. 寻找增广路,把路径上的边全部取反,得到一个更大的匹配$S`$

3. 重复第二部,直到图中不存在增广路.

关于具体怎么寻找增广路,怎么给路径取反,我讲在代码中解释.

模板题

代码:

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

struct edge
{
    int to,next;
}e[1000010];

int n,m,e_,size,ans;
int head[10010],match[10010];
bool flag[10010];

inline void EdgeAdd(int,int);
inline void Hungary();
inline bool find(int);

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d%d",&n,&m,&e_);
    for(int _=1;_<=e_;_++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        if(from>n||to>m||from>m||to>n)
        {
            continue;
        }
        EdgeAdd(from,to);
    }
    Hungary();
    printf("%d\n",ans);
return 0;
}

inline void EdgeAdd(int from,int to)
{
    e[++size].to=to;
    e[size].next=head[from];
    head[from]=size;
}

inline void Hungary()
{
    for(int _=1;_<=n;_++)//枚举左集中的结点
    {
        memset(flag,false,sizeof(flag));
        if(find(_)==true)//存在一条增广路
        {
            ans++;
        }
    }
}

inline bool find(int from)
{
    for(int _=head[from];_!=-1;_=e[_].next)//遍历该结点的路径
    {
        int to=e[_].to;
        if(flag[to]==false)//flag数组防止往回走
        {
            flag[to]=true;
            if(match[to]==0||find(match[to])==true)
/*这里有两种情况,一种是右集中的点没有被选,那么它们俩构成长度为1的增广路.
另一种是右集中的点已经被选了,但是往下递归可以发现选它的点可以有其他的选择,这样构成了一条两端都是非匹配点的路径,即增广路.
*/
            {
                match[to]=from;//更改匹配
                return true;
            }
        }
    }
return false;
}