自动搬运

查看原文

来自洛谷，原作者为

	Singercoder Our true self lies within.

搬运于2025-08-24 21:48:25，当前版本为作者最后更新于2020-04-30 14:11:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

不详细解释了，需要的可以看看别的题解。

主要思路就是用spfa判断入队次数是否>=n，如果是则说明有负环，这一点可以由spfa的松弛算法原理推导来。

注意一定要判入队次数而不是松弛次数，我看几乎现有每一篇题解判的都是松弛次数，可以试试这个hack。

hack原理很简单：如果存在重边导致了多次松弛，那么对松弛次数的判断就会产生影响。解决方式就是判入队次数，虽然略慢，但是更稳。

update[2020.7.26]：在写差分约束的时候想用spfa判无解，然后经过一系列的思考就有了下面这组新的hack数据：

input:
1
4 6
1 2 -3
1 3 -2
1 4 -1
2 3 -6
2 4 -5
3 4 -4
output:
NO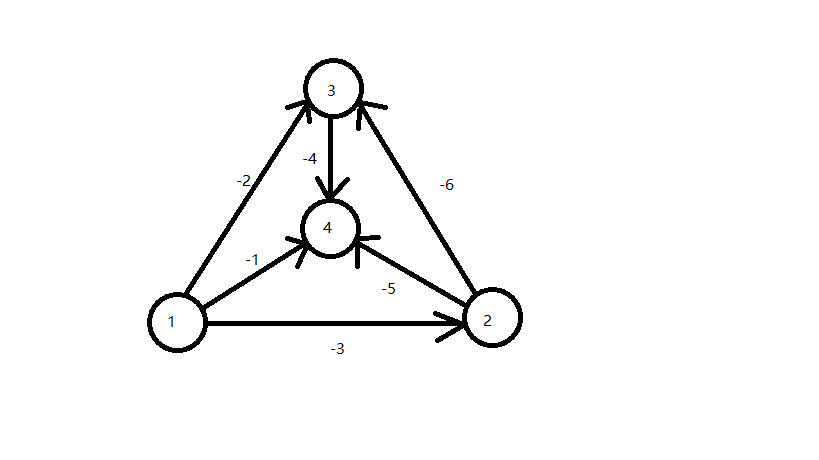

注意这组hack只对用链式前向星（而非vector）存边且判的是松弛次数（而非入队次数）的有效，而且该数据无重边无自环，比discuss里面的那个数据更有说服力。

首先hack原理就是对n号节点进行n-1轮松弛，每轮都有x($x \in [1,n-1]$）次松弛，这样就能产生n^2级别的松弛次数。

但是判入队次数就hack不掉了，每轮的第一次松弛会让n节点入队，但n节点只有在下一轮才会出队；因此本轮的其余所有松弛全部无法导致入队。

#include<cstdio>
#include<cstring>
#include<queue>
#define inf 0x3f3f3f3f
using namespace std;
const int MAXN=2010;
const int MAXM=3010;
int n,m;

int en=-1,eh[MAXN];
struct edge
{
	int u,v,w,next;
	edge(int U=0,int V=0,int W=0,int N=0):u(U),v(V),w(W),next(N){}
};edge e[MAXM<<1];
inline void add_edge(int u,int v,int w)
{
	e[++en]=edge(u,v,w,eh[u]);eh[u]=en;
}
void input()
{
	scanf("%d %d",&n,&m);
	en=-1;
	memset(eh,-1,sizeof(eh));
	int u,v,w;
	for(int i=1;i<=m;++i)
	{
		scanf("%d %d %d",&u,&v,&w);
		add_edge(u,v,w);
		if(w>=0)add_edge(v,u,w);
	}
}

int dis[MAXN],cnt[MAXN];
bool vis[MAXN];
queue<int> q;
void spfa()
{
	fill(dis+1,dis+n+1,inf);
	memset(cnt,0,sizeof(cnt));
	memset(vis,0,sizeof(vis));
	
	while(!q.empty())q.pop();
	dis[1]=0;vis[1]=1;q.push(1);
	
	int u,v,w;
	while(!q.empty())
	{
		u=q.front();vis[u]=0;q.pop();
		for(int i=eh[u];i!=-1;i=e[i].next)
		{
			v=e[i].v;w=e[i].w;
			if(dis[u]+w<dis[v])
			{
				dis[v]=dis[u]+w;
				if(!vis[v])
				{
					if(++cnt[v]>=n)//注意就是这个位置的判断。一定要保证在判vis之后，即判入队次数；而不是在判vis之前，即判松弛次数！！！
					{
						printf("YES\n");return;
					}
					vis[v]=1;q.push(v);
				}
			}
		}
	}
	printf("NO\n");
}

int main()
{
//	freopen("in.txt","r",stdin);
	int t;
	scanf("%d",&t);
	for(int i=1;i<=t;++i)
	{
		input();
		spfa();
	}
	return 0;
}

update[2020.7.28]：感谢AK新手村dalao提供的判最短路径边数的思路

在fyy2603提供的hack中，提到了极限数据可能爆int的问题，其原因在于要让入队次数达到上界n，则遍历边的总个数最大可达$n^2$。

考虑换一种思路，我们知道如果没有负环，从1号点到每个点的最短路径应当是不存在环的；而如果存在环那它只可能是负环，且最短路径长度会在算法过程中无限增大。

因此我们可以判断1号点到i号点的最短路径长度是否<n（即经过的点数<=n，没有任何一个点被重复经过），来更高效地判断是否存在负环。

而这也就完美避免了极限数据爆int的问题。（直接开ll不香吗）

//其他部分没有区别
void spfa()
{
	fill(dis+1,dis+n+1,inf);
	memset(cnt,0,sizeof(cnt));
	memset(vis,0,sizeof(vis));
	
	while(!q.empty())q.pop();
	dis[1]=0;vis[1]=1;q.push(1);
	
	int u,v,w;
	while(!q.empty())
	{
		u=q.front();vis[u]=0;q.pop();
		for(int i=eh[u];i!=-1;i=e[i].next)
		{
			v=e[i].v;w=e[i].w;
			if(dis[u]+w<dis[v])
			{
				dis[v]=dis[u]+w;
				cnt[v]=cnt[u]+1;//记录最短路径的边数 
				if(cnt[v]>=n)//最短路径边数>=n，即存在被重复遍历的点，也就是存在负环
				{
					printf("YES\n");
					return;
				}
				if(!vis[v])
				{
					vis[v]=1;q.push(v);
				}
			}
		}
	}
	printf("NO\n");
}