自动搬运

查看原文

来自洛谷，原作者为

	yedalong 注意力不够？刷题来凑！

搬运于2025-08-24 21:48:14，当前版本为作者最后更新于2025-03-18 22:52:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

其他题解有介绍 SPFA 的，这篇题解主要介绍 Dijkstra 的朴素版本和堆优化的。

什么是 Dijkstra

Dijkstra 算法由荷兰计算机科学家 E. W. Dijkstra 于 1956 年发现，1959 年公开发表。是一种求解非负权图上单源最短路径的算法。

朴素版本

首先先介绍 Dijkstra 的做法。 对于 $n$ 个点，我们需要将其分成两个部分。一部分中的点都已经找到了最短路径的长度，另一部分未找到。 假设有一张这样的图：
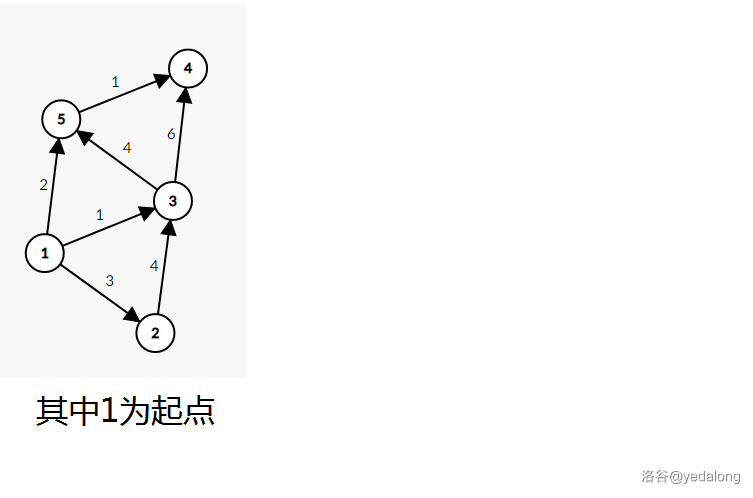
这里规定 $i$ 号点的 $dis$ 值为由 $s$ 到这个点的当前最短路径长度。
初始将所有点的最短路长度赋值为极大值。
从 $1$ 出发，我们首先先初始化从 $1$ 到 $1$ 的最短路 $dis_1=0$，并将 $1$ 点归到已找到最短路径的那一部分，然后我们对与它相连的每一条边都松弛一遍，更新 $dis_2=3,dis_3=1,dis_5=2$。接着我们从没有找到最短路径的那一堆点中寻找当前 $dis$ 值最小的，将那一点进行上述操作，这里找到的那个点就是 $3$，因为此时它的 $dis$ 值在未找到最短路径的那一堆点中是最小的，一直操作知道所有点都找到最短路径为止。
这种做法时间复杂度是 $O(n^2)$，不太优秀。。。

接下来稍微证明一下这样操作的正确性。
这里是用到了贪心的思想。
首先，我们先解释对于目前没有找到最短路径的那些点中为什么要将 $dis$ 值最小的那个点确定为已找到最短路径。这里先假设找到的那个点为 $v$。
首先我们先考虑从已找到最短路径的那些点走到 $v$ 是否还有更优解。由于我们松弛的那些边都是以已找到最短路径的那些点作为起点进行松弛的，那么其实当前的 $dis_v$ 已经是从已找到最短路径的那些点中松弛过来的最优情况，故这种情况无需继续考虑。
另外一种情况就是未找到最短路径的那些点走到 $v$ 是否还有更有解。这里先假设从一个未找到最短路径的点 $u$ 到点 $v$ 是更优解。对于正权边，从那些已找到最短路径的那些点走到 $v$ 再走到 $u$，至少要再经过两条边，因为边是非负的，因此走过来一定会大于原解，因此点 $u$ 不存在，即这种情况也是不可能出现的。
这里再稍微补充一下，第二种情况再某种情况下能达成，但是会满足 $dis_v<dis_u$，与最上头说的点 $v$ 为未找到最短路径的点中的 $dis$ 值最小的点不符，因此第二种情况在这种命题下不成立。
综上，此算法正确。

这里给出 $O(n^2)$ 朴素做法的代码：

void dijkstra(){
	for(int i = 1;i<=n;i++){//固定为每一次循环添加一个点 
		int k=0;//用于存未找到最短路径的那些点中的 dis 值最小者 
		for(int j = 1;j<=n;j++){//寻找 k 的过程，相信大佬们这部分都懂 
			if(!k&&!pd[j]){ 
				k=j;
				continue;
			}
			if(!pd[j]&&(dis[k]>dis[j])&&dis[j]!=2147483647) k=j;
		}
		pd[k]=1;//将 k 加入到已找到最短路径的那些点中 
		for(int j = 0;j<a[k].size();j++){
			dis[a[k][j].v]=min(dis[a[k][j].v],dis[k]+a[k][j].w);//松弛 
		}
	}
}

堆优化

优化的地方就是在上面的找 $k$ 的那个循环，考虑使用优先队列来存值。
其他地方也没啥区别了。
时间复杂度 $O(m\log m)$，还十分的稳定，超优秀的。
模板代码：

void dijkstra(){
	q.push({0,s});
	while(!q.empty()){
		if(pd[q.top().y]){
			q.pop();
			continue;
		}
		dis[q.top().y]=q.top().x;
		pd[q.top().y]=1;
		for(int j = 0;j<a[q.top().y].size();j++){
			q.push({q.top().x+a[q.top().y][j].w,a[q.top().y][j].v});
		}
		q.pop();
	}
}

注意：Dijkstra 只能用于非负边权的图中，否则无法保证其正确性

例题

算了，这里就不给大家一一列题了，有一个很好的最短路练习提单，大家可以去里面找题写。

哇，好辛苦啊，真的不点个关注再走吗 qwq