[ZJOI2013] 话旧

0
15011418730 LV 7 @ 2025-8-24 21:47:51
自动搬运

查看原文

来自洛谷，原作者为

awapwq233
Someday I'll Be Just Like You!

搬运于2025-08-24 21:47:51，当前版本为作者最后更新于2022-10-16 14:44:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P3336 [ZJOI2013]话旧题解

目前最优解 / 55ms

$\texttt{0x01}$ 形式化题意

自己看，懒得写。

反正就是只要开始往下走了就一定要走到 $0$ 。

$\texttt{0x02}$ 思路

把所有给过的点排个序，相邻的每两个点计算方案数，发现对之前的计算结果影响很小，故考虑 $\texttt{dp}$ 。

考虑到当前点向上向下走会对结果产生影响（就是形式化题意里面说的），因此将当前点向上 / 向下加入状态，于是我们设：

${f_i}$ 表示经过前 $i$ 个点且在第 $i$ 个点左导数 $F'(x_i)=1$ 的函数的个数。

${g_i}$ 表示经过前 $i$ 个点且在第 $i$ 个点左导数 $F'(x_i)=-1$ 的函数的个数。

值得注意的是，该函数一定经过 $(0, 0),(n, 0)$ ，记得把这两个点加上。

第一问答案即为 ${g_m}$ （ $m$ 已去重）。

第二问在转移的时候随手算算啦。

$\texttt{0x03 Q1}$

别忘了sort & unique。

对于两个相邻的点 $(x_1, y_1), (x_2, y_2)$ ，首先考虑其斜率 ${k}=\frac{y_2-y_1}{x_2-x_1}$ 。

显然的，当 $|k| > 1$ 时，函数不存在，此时第二问无解。

因此题目中默认 $|k|\in [0,1]$ ，应注意。

$\texttt{when k = 1:}$

那就只能上升啦？

${f_i = f_{i-1}}\ ?$

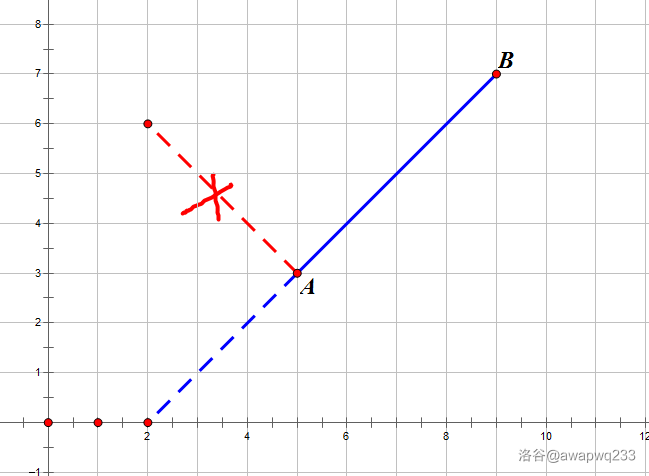
能不能由下降转为上升？

只要前面那个点 $F(x_{i-1}) = 0$ 就可以啦。

${f_i} =\Big\{^{ f_{i-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {(F(x_{i-1}) \neq 0)}} _{ f_{i-1} + g_{i - 1}\ \ \ \ \ {(F(x_{i-1}) = 0)}}$

$\texttt{when k = -1:}$

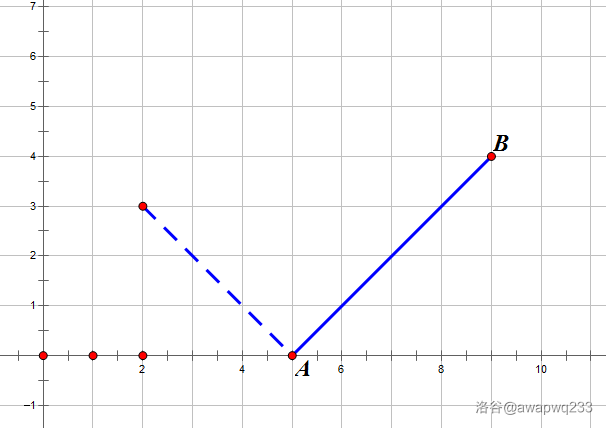
上升下降都可以啦。

${g_i = f_{i-1} + g_{i-1}}$

$\texttt{when k} \in \texttt{[0,1):}$

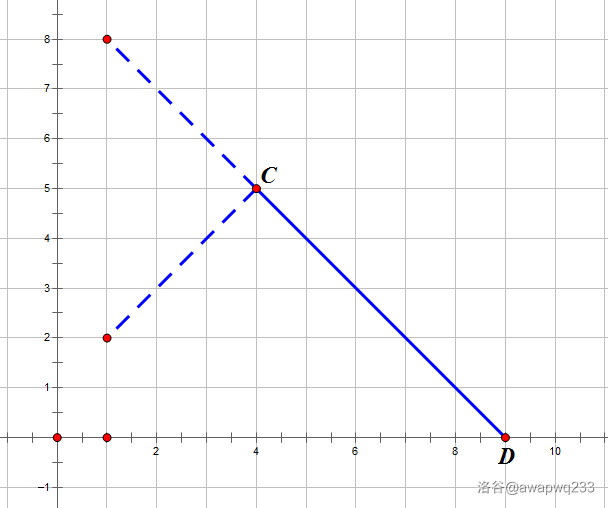
你要想一下：如果按照贪心的思路一直向下，能不能碰到最底下？

为什么要这么想呢？

    如果不能碰到：只能在上面出现拐点，且拐点 & 路径唯一。

        这很好想叭。要是开始往下就不能回头了。其他地方必定会错过那个点。

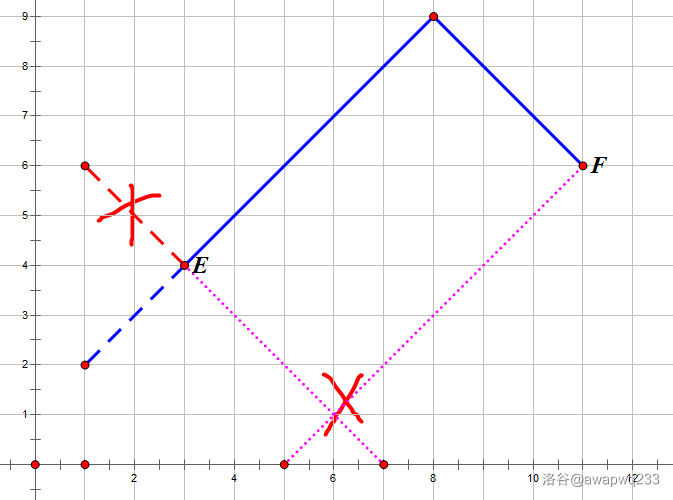
    如果刚好碰到：上面下面两条路，均唯一。

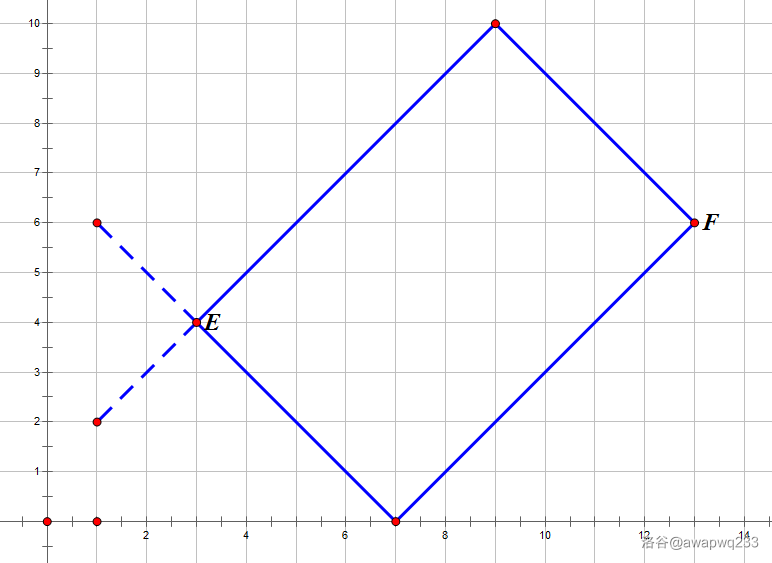
    如果很早就能碰到：好多好多好多好多好多好多

接着分类讨论。那么如何区分这几种情况呢？

注意到我们画的图：两个点总是尽可能向下走与 $x$ 轴相交。

一般的，对于 $(x_{i-1}, y_{i-1}),(x_i, y_i)$ ，分别代入 $y=-x+b_1,y=x+b_2$ ，有 $b_1=x_{i-1}+y_{i-1}, b_2=-x_i+y_i$ ，截距分别为 $-\frac{b_1}{k_1}=x_{i-1}+y_{i-1},-\frac{b_2}{k_2}=x_{i}-y_{i}$，二者作差，得

$l = x_i-y_i-x_{i-1}-y_{i-1}$

这就是分类讨论的依据。

$\texttt{when l < 0:}$

${g_i} =\Big\{^{ f_{i-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {(F(x_{i-1}) \neq 0)}} _{ f_{i-1} + g_{i - 1}\ \ \ \ \ {(F(x_{i-1}) = 0)}}$

和上面类似，自己想。

$\texttt{when l = 0:}$

${f_i = f_{i-1} + g_{i-1}}$

${g_i} =\Big\{^{ f_{i-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {(F(x_{i-1}) \neq 0)}} _{ f_{i-1} + g_{i - 1}\ \ \ \ \ {(F(x_{i-1}) = 0)}}$

和上面类似，懒得写。

$\texttt{when l > 0:}$

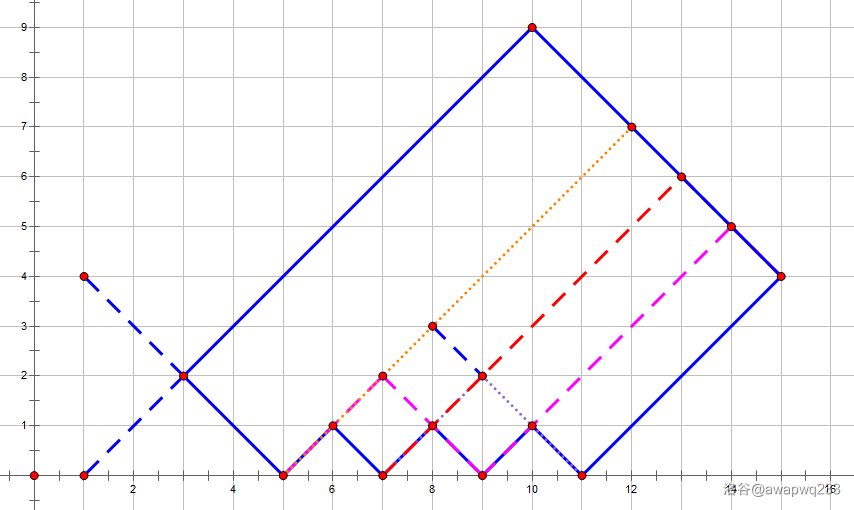
观察可以发现， $(x-1,0)\to(x,1)\to(x+1,0)$ 的小结构（我们称它为“齿”）的个数为 $\frac{l}{2}$ 。

每次选定一个“齿”，将其往上翻，我们都可以得到一条新的路径。

设方案数为 $k$ ：

如果初始点为上升： $k=2^{\frac{l}{2}}$

如果初始点为下降： $k=2^{\frac{l}{2}-1}$ ，因为第一个向下的齿不能向上翻转，它必须碰到最下面。

${f_i} =\Big\{^{ f_{i-1}\times 2^{\frac{l}{2}}+g_{i-1}\times 2^{\frac{l}{2}-1} \ \ \ \ \ \ \ \ \ {(F(x_{i}) \neq 0)}} _{0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {(F(x_{i}) = 0)}}$

$g_i=f_{i-1}\times 2^{\frac{l}{2}}+g_{i-1}\times 2^{\frac{l}{2}-1}$

$\texttt{0x04 Q2}$

第二问的话，贪心就好啦。

但是如果正在往下走的话贪心会寄。判断一下。

$\texttt{0x05 Code}$

代码美学。
```
int main()
{
	read(n, m);
	F(i, 1, m) P[i].input();
	P[++ m].input(0, 0), P[++ m].input(n, 0);
	sort(P + 1, P + m + 1); m = unique(P + 1, P + m + 1) - P - 1;
	g[1] = 1;
	F(i, 2, m)
	{
		int l = b.x - b.y - a.x - a.y >> 1;
		if(a.x - b.x == a.y - b.y) 		f[i] = (f[i - 1] + (a.y ? 0 : g[i - 1])) % mod;
		else if(a.x - b.x == b.y - a.y) g[i] = (f[i - 1] + (g[i - 1])) % mod;
		else if(l < 0) 					g[i] = (f[i - 1] + (a.y ? 0 : g[i - 1])) % mod;
		else if(l == 0)					f[i] = (f[i - 1] + (g[i - 1])) % mod,
										g[i] = (f[i - 1] + (a.y ? 0 : g[i - 1])) % mod;
		else 
		{
			int k = fastpow(2, l - 1, mod);
			if(b.y) f[i] = 1ll * ((f[i - 1] << 1) + g[i - 1]) * k % mod;
					g[i] = 1ll * ((f[i - 1] << 1) + g[i - 1]) * k % mod;
		}
		if(g[i] || !b.y) ans = qmax(ans, b.y, b.x + b.y - a.x + a.y >> 1);
	}
	write(' ', g[m], ans);
	return 0;
}
```
三目运算符要是再不打括号 $awa$ 就吃了自己吧。