1 条题解
-
0
自动搬运
来自洛谷,原作者为

DDOSvoid
**搬运于
2025-08-24 21:47:43,当前版本为作者最后更新于2018-09-27 11:37:16,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
思路:
发现 k 很小,所以分类讨论一波
直接输出就行了
枚举中间点
void solve_3(){ for(int i = 1; i <= n; ++i){ int u = i; c2 = 0; for(int j = head[u]; ~j; j = e[j].next){ int v = e[j].to; a[++c2] = v; } for(int j = 1; j <= c2; ++j) for(int k = 1; k < j; ++k) ans[a[j]][a[k]] = ans[a[k]][a[j]] = 1; } }复杂度
先枚举两端点 和 ,然后再枚举里面的两个点 和 即可。复杂度 ,因为每对边被枚举了 次
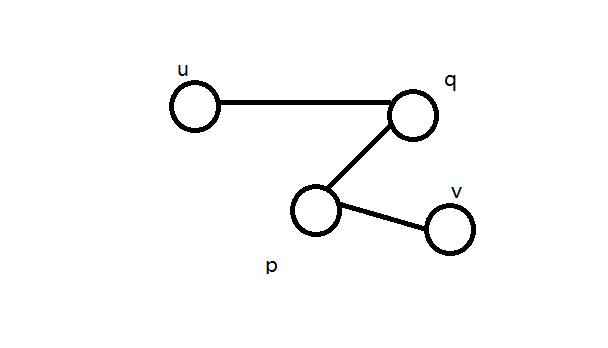
先来个图
发现这样的 是合法的。也就是说,对于两个不同的点 和 以及和 相连的点 还有与 相连的点 ,如果 和 之间还有一点 ,且 和 相连, 和 相连,那么 就是合法的
首先枚举 和 ,然后枚举中间点 ,记录中间点个数和 表示 是否能作为中间点。然后再枚举 和 ,判断是否除了 和 之外还有别的点可以作为中间点,这个只需判断 是否大于 0 即可
复杂度还是
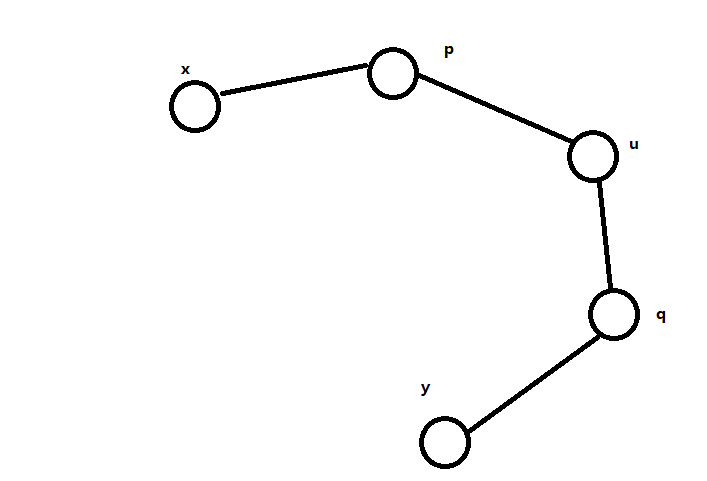
void solve_5(){ for(int p = 1; p <= n; ++p) for(int q = 1; q < p; ++q){ int sum = 0; for(int i = head[p]; ~i; i = e[i].next){ int u = e[i].to; if(u == q || !g[u][q]) continue; cnt[u] = 1; ++sum; } for(int l = head[p]; ~l; l = e[l].next){ int x = e[l].to; if(x == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int y = e[r].to; if(y == p || y == x) continue; ans[y][x] = (ans[x][y] |= sum - cnt[x] - cnt[y] > 0); } } for(int i = head[p]; ~i; i = e[i].next){ int u = e[i].to; if(u == q) continue; cnt[u] = 0; } } }方法其实类似 看图
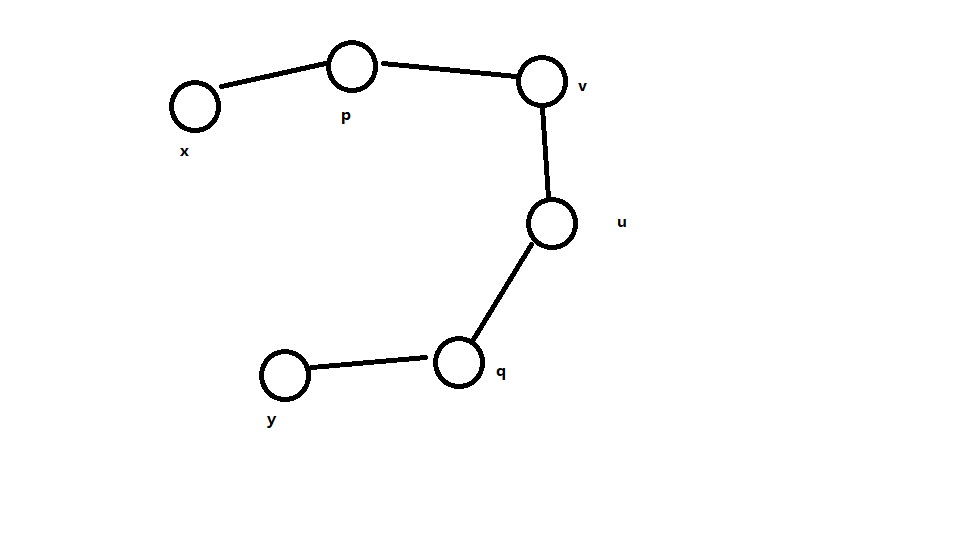
还是枚举 和 ,然后枚举 和 ,我们统计出现在中间路径的总条数和 表示 出现在中间路径的次数
然后在枚举 和 ,只要满足 比较简单的容斥
复杂度依然是
for(int p = 1; p <= n; ++p) for(int q = 1; q < p; ++q){ int sum = 0; for(int l = head[p]; ~l; l = e[l].next){ int u = e[l].to; if(u == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int v = e[r].to; if(v == p || u == v || !g[u][v]) continue; ++cnt[u]; ++cnt[v]; ++sum; } } for(int l = head[p]; ~l; l = e[l].next){ int x = e[l].to; if(x == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int y = e[r].to; if(y == p || x == y) continue; ans[y][x] = (ans[x][y] |= sum - cnt[x] - cnt[y] + g[x][y] > 0); } } for(int l = head[p]; ~l; l = e[l].next){ int u = e[l].to; if(u == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int v = e[r].to; if(v == p || u == v || !g[u][v]) continue; cnt[u] = cnt[v] = 0; } } }这种情况就比较麻烦了,但是总的方法还是不变的
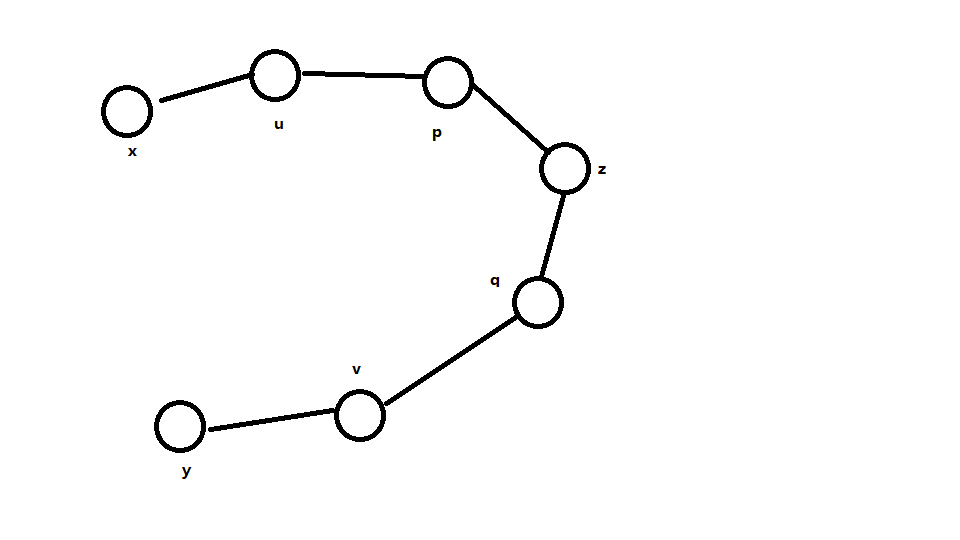
首先预处理出所有三元组
然后我们这次枚举 ,然后在枚举三元组,统计中间三元组的个数和 表示 u 在三元组中出现的次数, 表示 u 和 v 在三元组中作为边上的两个的方案数即 和 , 表示 在 的位置, 在 的位置的方案数
再枚举 和 ,只要满足 $sum-cnt[x]-cnt[y]+cnt1[x][y]+cnt2[x][y]+cnt2[y][x]>0$
复杂度== 和 只是方便不用每次都置零
void solve_7(){ memset(vis1, 0, sizeof vis1); memset(vis2, 0, sizeof vis2); I = 0; for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) b[i][j].clear(); for(int i = 1; i <= n; ++i){ int u = i; c2 = 0; for(int j = head[u]; ~j; j = e[j].next){ int v = e[j].to; a[++c2] = v; } for(int j = 1; j <= c2; ++j) for(int k = 1; k < j; ++k){ b[a[j]][a[k]].pb(i); b[a[k]][a[j]].pb(i); } } for(int u = 1; u <= n; ++u) for(int v = 1; v < u; ++v){ int sum = 0; ++I; c3 = 0; for(int i = head[u]; ~i; i = e[i].next){ int p = e[i].to; if(p == v) continue; for(int j = head[v]; ~j; j = e[j].next){ int q = e[j].to; if(q == u || p == q) continue; for(int k = 0, _s = b[p][q].size(); k < _s; ++k){ int z = b[p][q][k]; if(z == u || z == v) continue; c[++c3] = z; if(vis1[p][q] == I) ++cnt1[p][q]; else vis1[p][q] = I, cnt1[p][q] = 1; if(vis2[p][z] == I) ++cnt2[p][z]; else vis2[p][z] = I, cnt2[p][z] = 1; if(vis2[q][z] == I) ++cnt2[q][z]; else vis2[q][z] = I, cnt2[q][z] = 1; ++cnt[q]; ++cnt[p]; ++cnt[z]; ++sum; } } } for(int i = head[u]; ~i; i = e[i].next){ int p = e[i].to; if(p == v) continue; for(int j = head[v]; ~j; j = e[j].next){ int q = e[j].to; if(q == u || p == q) continue; if(vis1[p][q] != I) cnt1[p][q] = 0; if(vis2[p][q] != I) cnt2[p][q] = 0; if(vis2[q][p] != I) cnt2[q][p] = 0; ans[p][q] |= (sum - cnt[p] - cnt[q] + cnt1[p][q] + cnt2[p][q] + cnt2[q][p] > 0); ans[q][p] = ans[p][q]; } } for(int i = 1; i <= c3; ++i) cnt[c[i]] = 0; for(int i = head[u]; ~i; i = e[i].next) cnt[e[i].to] = 0; for(int i = head[v]; ~i; i = e[i].next) cnt[e[i].to] = 0; } }AC 代码
#include<iostream> #include<cstdio> #include<cstring> #include<vector> #define maxn 1010 #define maxm 5010 #define pb push_back using namespace std; int T, n, m, K; int u[maxm], v[maxm]; struct Edge{ int to, next; }e[maxm * 2]; int c1, head[maxn]; inline void add_edge(int u, int v){ e[c1].to = v; e[c1].next = head[u]; head[u] = c1++; } int g[maxn][maxn]; bool ans[maxn][maxn]; void put(){ for(int i = 1; i <= n; ++i, putchar('\n')) for(int j = 1; j <= n; ++j){ if(ans[i][j]) putchar('Y'); else putchar('N'); ans[i][j] = 0; } } void solve_2(){ for(int i = 1; i <= n; ++i) for(int j = head[i]; ~j; j = e[j].next) ans[i][e[j].to] = 1; } int a[maxn], c2; void solve_3(){ for(int i = 1; i <= n; ++i){ int u = i; c2 = 0; for(int j = head[u]; ~j; j = e[j].next){ int v = e[j].to; a[++c2] = v; } for(int j = 1; j <= c2; ++j) for(int k = 1; k < j; ++k) ans[a[j]][a[k]] = ans[a[k]][a[j]] = 1; } } void solve_4(){ for(int i = 1; i <= n; ++i) for(int j = 1; j < i; ++j){ bool F = 0; for(int l = head[i]; ~l && !F; l = e[l].next){ int v1 = e[l].to; if(v1 == j) continue; for(int r = head[j]; ~r; r = e[r].next){ int v2 = e[r].to; if(v2 == i || v2 == v1) continue; if(g[v1][v2]){F = 1; break;} } } ans[i][j] = ans[j][i] = F; } } int cnt[maxn]; void solve_5(){ for(int p = 1; p <= n; ++p) for(int q = 1; q < p; ++q){ int sum = 0; for(int i = head[p]; ~i; i = e[i].next){ int u = e[i].to; if(u == q || !g[u][q]) continue; cnt[u] = 1; ++sum; } for(int l = head[p]; ~l; l = e[l].next){ int x = e[l].to; if(x == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int y = e[r].to; if(y == p || y == x) continue; ans[y][x] = (ans[x][y] |= sum - cnt[x] - cnt[y] > 0); } } for(int i = head[p]; ~i; i = e[i].next){ int u = e[i].to; if(u == q) continue; cnt[u] = 0; } } } void solve_6(){ for(int p = 1; p <= n; ++p) for(int q = 1; q < p; ++q){ int sum = 0; for(int l = head[p]; ~l; l = e[l].next){ int u = e[l].to; if(u == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int v = e[r].to; if(v == p || u == v || !g[u][v]) continue; ++cnt[u]; ++cnt[v]; ++sum; } } for(int l = head[p]; ~l; l = e[l].next){ int x = e[l].to; if(x == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int y = e[r].to; if(y == p || x == y) continue; ans[y][x] = (ans[x][y] |= sum - cnt[x] - cnt[y] + g[x][y] > 0); } } for(int l = head[p]; ~l; l = e[l].next){ int u = e[l].to; if(u == q) continue; for(int r = head[q]; ~r; r = e[r].next){ int v = e[r].to; if(v == p || u == v || !g[u][v]) continue; cnt[u] = cnt[v] = 0; } } } } vector<int> b[maxn][maxn]; int cnt1[maxn][maxn], cnt2[maxn][maxn], I; int vis1[maxn][maxn], vis2[maxn][maxn]; int c[maxm], c3; void solve_7(){ memset(vis1, 0, sizeof vis1); memset(vis2, 0, sizeof vis2); I = 0; for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) b[i][j].clear(); for(int i = 1; i <= n; ++i){ int u = i; c2 = 0; for(int j = head[u]; ~j; j = e[j].next){ int v = e[j].to; a[++c2] = v; } for(int j = 1; j <= c2; ++j) for(int k = 1; k < j; ++k){ b[a[j]][a[k]].pb(i); b[a[k]][a[j]].pb(i); } } for(int u = 1; u <= n; ++u) for(int v = 1; v < u; ++v){ int sum = 0; ++I; c3 = 0; for(int i = head[u]; ~i; i = e[i].next){ int p = e[i].to; if(p == v) continue; for(int j = head[v]; ~j; j = e[j].next){ int q = e[j].to; if(q == u || p == q) continue; for(int k = 0, _s = b[p][q].size(); k < _s; ++k){ int z = b[p][q][k]; if(z == u || z == v) continue; c[++c3] = z; if(vis1[p][q] == I) ++cnt1[p][q]; else vis1[p][q] = I, cnt1[p][q] = 1; if(vis2[p][z] == I) ++cnt2[p][z]; else vis2[p][z] = I, cnt2[p][z] = 1; if(vis2[q][z] == I) ++cnt2[q][z]; else vis2[q][z] = I, cnt2[q][z] = 1; ++cnt[q]; ++cnt[p]; ++cnt[z]; ++sum; } } } for(int i = head[u]; ~i; i = e[i].next){ int p = e[i].to; if(p == v) continue; for(int j = head[v]; ~j; j = e[j].next){ int q = e[j].to; if(q == u || p == q) continue; if(vis1[p][q] != I) cnt1[p][q] = 0; if(vis2[p][q] != I) cnt2[p][q] = 0; if(vis2[q][p] != I) cnt2[q][p] = 0; ans[p][q] |= (sum - cnt[p] - cnt[q] + cnt1[p][q] + cnt2[p][q] + cnt2[q][p] > 0); ans[q][p] = ans[p][q]; } } for(int i = 1; i <= c3; ++i) cnt[c[i]] = 0; for(int i = head[u]; ~i; i = e[i].next) cnt[e[i].to] = 0; for(int i = head[v]; ~i; i = e[i].next) cnt[e[i].to] = 0; } } void work(){ memset(head, -1, sizeof head); c1 = 0; scanf("%d%d%d", &n, &m, &K); for(int i = 1; i <= m; ++i){ int x, y; scanf("%d%d", &x, &y); add_edge(x, y); add_edge(y, x); g[x][y] = g[y][x] = 1; u[i] = x; v[i] = y; } switch(K){ case 2 : solve_2(); break; case 3 : solve_3(); break; case 4 : solve_4(); break; case 5 : solve_5(); break; case 6 : solve_6(); break; case 7 : solve_7(); break; } put(); for(int i = 1; i <= m; ++i) g[u[i]][v[i]] = g[v[i]][u[i]] = 0; } int main(){ scanf("%d", &T); while(T--) work(); }
- 1
信息
- ID
- 2396
- 时间
- 4000ms
- 内存
- 512MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
