自动搬运

查看原文

来自洛谷，原作者为

	Fading AFO

搬运于2025-08-24 21:47:38，当前版本为作者最后更新于2018-10-09 11:03:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

默认大家都会树剖。

动态开点线段树？

其实和主席树差不多。

主席树就是动态开点的。

我们对于这个题目，对于每一个宗教建一个线段树。每棵线段树存区间最大值$(max)$和区间和$(tot)$。

这不是树上询问吗？？？树剖就好了qwq

你说空间开不下？所以我们要动态开点。

什么意思呢？

简单点说，不需要的线段树节点不添加，只添加需要的线段树节点。

比如说有两个宗教，一个是%$czx$教，一个是嘲讽$xj$教(???

城市分布是这样的：

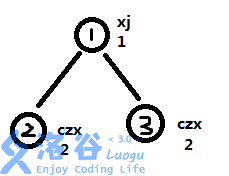
城市里的数字表示$DFS$序，不是编号！我们的线段树下标和$DFS$序有关！

城市宗教下方的数字表示评级。

对于第$1$个城市,我们把它加入关于$xj$的线段树中，因为线段树还没有节点表示的区间覆盖$1$这个点，所以我们新建一个节点$(tot=1,max=1)$:

然后像线段树的单点修改一样，向下传递,传递到$[1,2]$，没有节点覆盖，新建！

向下传递,传递到$[1,1]$，没有节点覆盖，新建！

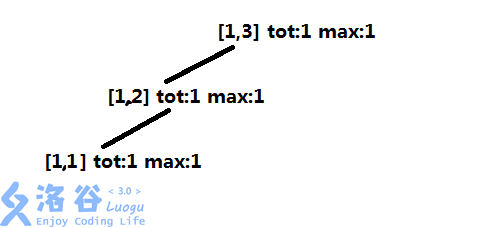
就是这样！每一次添加的节点数最多是$logn$级别的。

为什么?因为线段树是一个完全二叉树，每一次最多遍历$(logn) +1$个节点。

所以空间复杂度就是$O(nlogn)$

然后我们还需要什么？因为我们对于每一个宗教都要开一颗线段树，所以我们要开一个$root$数组，记录每一棵线段树的根。我们还需要一个变量记录当前有多少个节点。

int root[100004],len;
struct Node{
	int l,r,max,tot;//l是左儿子的编号,r是右儿子的编号
}tree[20000110];
inline void update(int &rt,int w,int l,int r,int pos){//w是评级,pos你要添加的点的DFS序
	if (!rt) rt=++len;
	tree[rt].max=max(tree[rt].max,w),tree[rt].tot+=w;
	if (l==r) return; int mid=(l+r)/2;
	if (mid>=pos) update(tree[rt].l,w,l,mid,pos);
	else update(tree[rt].r,w,mid+1,r,pos);
}

然后对于修改操作，比如把$DFS$序为$x$的点宗教改为$y$，就先在原先$x$对应宗教对应的线段树中把[x,x]的节点的值全该成$0$，然后对于它到根节点的路径上的所有解点$pushup$一下。

即

inline void remove(int &rt,int l,int r,int pos){
	if (l==r){ tree[rt].tot=0,tree[rt].max=0;return; }
	int mid=(l+r)/2;
	if (mid>=pos) remove(tree[rt].l,l,mid,pos);
	else remove(tree[rt].r,mid+1,r,pos);
	tree[rt].tot=tree[tree[rt].l].tot+tree[tree[rt].r].tot;
	tree[rt].max=max(tree[tree[rt].l].max,tree[tree[rt].r].max);
}

最后在$y$对应的线段树中$update\ x$的评级

查询的话就在两个节点的路径上跳链就可以了。

但是查询一条链上的值怎么办呢？

设旅行者的宗教是$X$，两个点的$DFS$序分别为$A,B$，这就等价于查询$X$所对应的线段树区间$[A,B]$的值。

inline int querytot(int rt,int lb,int rb,int l,int r){
	if (r<lb||l>rb) return 0;
	if (r>=rb&&l<=lb) return tree[rt].tot;
	int mid=(lb+rb)/2;
	return querytot(tree[rt].l,lb,mid,l,r)+querytot(tree[rt].r,mid+1,rb,l,r);
}
inline int querymax(int rt,int lb,int rb,int l,int r){
	if (r<lb||l>rb) return 0;
	if (r>=rb&&l<=lb) return tree[rt].max;
	int mid=(lb+rb)/2;
	return max(querymax(tree[rt].l,lb,mid,l,r),querymax(tree[rt].r,mid+1,rb,l,r));
}
inline int sigmax(int u,int v,int zj){
	int ans=0;
	while (top[u]!=top[v]){
		if (dep[top[u]]<dep[top[v]]) swap(u,v);
		ans=max(ans,querymax(root[zj],1,n,tpos[top[u]],tpos[u]));
		u=fa[top[u]];
	}
	if (dep[u]<dep[v]) swap(u,v);
	ans=max(ans,querymax(root[zj],1,n,tpos[v],tpos[u]));
	return ans;
}
inline int sigtot(int u,int v,int zj){
	int ans=0;
	while (top[u]!=top[v]){
		if (dep[top[u]]<dep[top[v]]) swap(u,v);
		ans=ans+querytot(root[zj],1,n,tpos[top[u]],tpos[u]);
		u=fa[top[u]];
	}
	if (dep[u]<dep[v]) swap(u,v);
	ans=ans+querytot(root[zj],1,n,tpos[v],tpos[u]);
	return ans;
}

完整代码:

#include<bits/stdc++.h>
using namespace std;
struct node{
    int to,next;
}g[1000000];
int tot,n,m,cnt,w[100004],zj[100004],len,head[100004],dep[100004],wson[100004],top[100004],tpos[100004],pre[100004],fa[100004],size[100004];
inline void made(int from,int to){
    g[++tot].to=to;
    g[tot].next=head[from];
    head[from]=tot;
}
inline void dfs1(int rt,int ff){
    fa[rt]=ff;dep[rt]=dep[ff]+1;size[rt]=1;
    for (int i=head[rt];i;i=g[i].next){
        int v=g[i].to;
        if (v==ff) continue;
        dfs1(v,rt);
        size[rt]+=size[v];
        if (!wson[rt]||size[wson[rt]]<size[v]) wson[rt]=v;
    }
}
inline void dfs2(int rt,int tops){
    tpos[rt]=++cnt;pre[cnt]=rt;top[rt]=tops;
    if (wson[rt]) dfs2(wson[rt],tops);
    for (int i=head[rt];i;i=g[i].next){
        int v=g[i].to;
        if (v==fa[rt]||v==wson[rt]) continue;
        dfs2(v,v);
    }
}
int root[100004];
struct Node{
    int l,r,max,tot;
}tree[20000110];
inline void update(int &rt,int w,int l,int r,int pos){
    if (!rt) rt=++len;
    tree[rt].max=max(tree[rt].max,w),tree[rt].tot+=w;
    if (l==r) return; int mid=(l+r)/2;
    if (mid>=pos) update(tree[rt].l,w,l,mid,pos);
    else update(tree[rt].r,w,mid+1,r,pos);
}
inline void remove(int &rt,int l,int r,int pos){
    if (l==r){ tree[rt].tot=0,tree[rt].max=0;return; }
    int mid=(l+r)/2;
    if (mid>=pos) remove(tree[rt].l,l,mid,pos);
    else remove(tree[rt].r,mid+1,r,pos);
    tree[rt].tot=tree[tree[rt].l].tot+tree[tree[rt].r].tot;
    tree[rt].max=max(tree[tree[rt].l].max,tree[tree[rt].r].max);
}
inline int querytot(int rt,int lb,int rb,int l,int r){
    if (r<lb||l>rb) return 0;
    if (r>=rb&&l<=lb) return tree[rt].tot;
    int mid=(lb+rb)/2;
    return querytot(tree[rt].l,lb,mid,l,r)+querytot(tree[rt].r,mid+1,rb,l,r);
}
inline int querymax(int rt,int lb,int rb,int l,int r){
    if (r<lb||l>rb) return 0;
    if (r>=rb&&l<=lb) return tree[rt].max;
    int mid=(lb+rb)/2;
    return max(querymax(tree[rt].l,lb,mid,l,r),querymax(tree[rt].r,mid+1,rb,l,r));
}
inline int sigmax(int u,int v,int zj){
    int ans=0;
    while (top[u]!=top[v]){
        if (dep[top[u]]<dep[top[v]]) swap(u,v);
        ans=max(ans,querymax(root[zj],1,n,tpos[top[u]],tpos[u]));
        u=fa[top[u]];
    }
    if (dep[u]<dep[v]) swap(u,v);
    ans=max(ans,querymax(root[zj],1,n,tpos[v],tpos[u]));
    return ans;
}
inline int sigtot(int u,int v,int zj){
    int ans=0;
    while (top[u]!=top[v]){
        if (dep[top[u]]<dep[top[v]]) swap(u,v);
        ans=ans+querytot(root[zj],1,n,tpos[top[u]],tpos[u]);
        u=fa[top[u]];
    }
    if (dep[u]<dep[v]) swap(u,v);
    ans=ans+querytot(root[zj],1,n,tpos[v],tpos[u]);
    return ans;
}
char s[100];
int main(){
    len=0;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++){
        scanf("%d%d",&w[i],&zj[i]);
    }
    int x,y;
    for (int i=1;i<n;i++){
        scanf("%d%d",&x,&y);
        made(x,y);made(y,x);
    }
    dfs1(1,0);dfs2(1,1);
    for (int i=1;i<=n;i++){
        update(root[zj[i]],w[i],1,n,tpos[i]);
    }		
    while (m--){
        scanf("%s",s);scanf("%d%d",&x,&y);
        switch (s[1]){
            case 'C':{
                remove(root[zj[x]],1,n,tpos[x]);
                update(root[y],w[x],1,n,tpos[x]);
                zj[x]=y;
                break;
            }
            case 'W':{
                remove(root[zj[x]],1,n,tpos[x]);
                update(root[zj[x]],y,1,n,tpos[x]);
                w[x]=y;
                break;
            }
            case 'S':{
                printf("%d\n",sigtot(x,y,zj[x]));
                break;
            } 
            case 'M':{
                printf("%d\n",sigmax(x,y,zj[x]));
                break;
            }
        }
    }
    return 0;
}