自动搬运

查看原文

来自洛谷，原作者为

	hsfzLZH1 我永远喜欢珂朵莉

搬运于2025-08-24 21:47:22，当前版本为作者最后更新于2018-08-15 15:36:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意：有一个行列的棋盘，每个格子上有三种可能的情况：落白子($W$)，落黑子($B$)和无子($X$)。所有可能的棋盘状态共有$3^{n\times m}$种。有$Q$次询问，每次询问给出一个$2$行$c$列的矩阵，问有多少种棋盘，使得其至少有一个子矩阵与该矩阵完全相同。

利用补集转化的思想，把问题转换为求没有任何一个子矩阵满足匹配条件的棋盘的种数$ans$。最后的答案即为$3^{n\times m}-ans$。 使用轮廓线$DP$解决这个问题。设$f_{x,y,k,i,j}$表示当前考虑到第$x$行第$y$列，上面的轮廓线状态为$i$，矩阵第一行匹配的位置为$j$，第二行匹配位置为的方案总数$k$。（轮廓线状态表示当前点能否匹配到模板串第一行的末尾，也就是和下图红色区域的匹配状态）

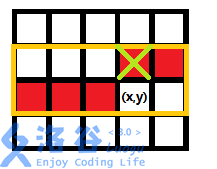
$x$和$y$这两维可以不存，滚动。对于所有$x$和$y$，初始状态为$f_{x,y,0,0,0}=1$。计算到新的一行时，所有上一行的$f_{x-1,y,i,j,k}$都要转移到$f_{x,y,0,0,0}$。 利用$KMP$进行转移。预处理出询问矩阵两行的失配函数，记为$nxt_{0,x}$和$nxt_{1,x}$。同时预处理出模式串位置$x$对应的文本串位置上的值是$v$的话的失配函数，记为$t_{0,x,v}$和$t_{1,x,v}$。转移的过程中，当$i$和$j$达到$c$时，很显然存在这样的匹配，应该删掉这种情况，此时值应设为$0$；其他时候，将$i$或$j$沿着失配边向前跳一下。

时间复杂度为$O(nm\times 2^m \times c^2)$。

代码展示：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=1000000007;
const int maxn=7;
const int maxv=1<<12;
int n,m,c,Q,maxx,a1[maxn],a2[maxn],nxt1[maxn],nxt2[maxn],t1[maxn][3],t2[maxn][3],f[2][maxv][maxn][maxn],cur,ans;
char s1[maxn],s2[maxn];
inline int getid(char x)
{
	if(x=='W')return 0;
	if(x=='B')return 1;
	if(x=='X')return 2;
}
int powmod(int a,int k)
{
	ll ret=1,x=a;
	while(k)
	{
		if(k&1)ret=ret*x%mod;
		x=x*x%mod;
		k>>=1;
	}
	return (int)ret;
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&c,&Q);
	maxx=1<<(m-c+1);
	while(Q--)
	{
		scanf("%s%s",s1+1,s2+1);
		for(int i=1;i<=c;i++)a1[i]=getid(s1[i]),a2[i]=getid(s2[i]);
		for(int i=2,j=0;i<=c;i++)
		{
			while(j&&a1[j+1]!=a1[i])j=nxt1[j];
			if(a1[j+1]==a1[i])j++;
			nxt1[i]=j;
		}
		for(int i=2,j=0;i<=c;i++)
		{
			while(j&&a2[j+1]!=a2[i])j=nxt2[j];
			if(a2[j+1]==a2[i])j++;
			nxt2[i]=j;	
		}
		for(int i=0;i<c;i++)for(int j=0,k=i;j<3;j++,k=i)
		{
			while(k&&a1[k+1]!=j)k=nxt1[k];
			if(a1[k+1]==j)k++;
			t1[i][j]=k;
		}
		for(int i=0;i<c;i++)for(int j=0,k=i;j<3;j++,k=i)
		{
			while(k&&a2[k+1]!=j)k=nxt2[k];
			if(a2[k+1]==j)k++;
			t2[i][j]=k;
		}
		memset(f[0],0,sizeof f[0]);
		f[0][0][0][0]=1;cur=1;
		for(int i=1;i<=n;i++)
		{
			memset(f[cur],0,sizeof f[cur]);
			for(int j=0;j<maxx;j++)for(int a=0;a<c;a++)
			for(int b=0;b<c;b++)f[cur][j][0][0]+=f[1-cur][j][a][b],f[cur][j][0][0]%=mod;
			cur=1-cur;
			for(int j=1;j<=m;j++)
			{
				memset(f[cur],0,sizeof f[cur]);
				for(int k=0;k<maxx;k++)for(int a=0;a<c;a++)
				for(int b=0;b<c;b++)if(f[1-cur][k][a][b])
				for(int col=0;col<3;col++)
				{
					int pa=t1[a][col],pb=t2[b][col],S=k;
					if(j>=c)if((S>>j-c)&1)S^=1<<j-c;
					if(pa==c){S^=1<<j-c;pa=nxt1[c];}
					if(pb==c){if((k>>j-c)&1)continue;pb=nxt2[c];}
					f[cur][S][pa][pb]+=f[1-cur][k][a][b];
					f[cur][S][pa][pb]%=mod;
				}
				cur=1-cur;
			}
		}
		ans=powmod(3,n*m);
		for(int i=0;i<maxx;i++)for(int j=0;j<c;j++)for(int k=0;k<c;k++)
		ans=(ans-f[1-cur][i][j][k]%mod+mod)%mod;
		printf("%d\n",ans);
	}
	return 0;
}