自动搬运

查看原文

来自洛谷，原作者为

	cmd2001 rm -rf ~

搬运于2025-08-24 21:47:12，当前版本为作者最后更新于2018-04-14 23:38:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题让我爆肝啦......

这种计数显然容斥，正好不含任何坏点的我们不会算，但是我们能算至少含零个坏点的，至少含一个坏点的，至少含两个坏点的......

所以最终的答案就是(至少含零个坏点的-至少含一个坏点的+至少含两个坏点的-至少含三个坏点的+至少含四个坏点的)。

然后就是怎么计算的问题。

对于至少含零个坏点的，我们不妨设定所有点都是好点。

对于非正放的正方形，我们能找到一个正好包含它的最小的正放的正方形，显然这样的正方形是唯一的。

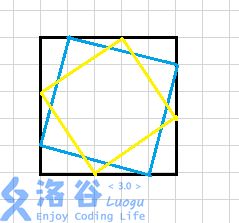
然后我们让四个点在这个正方形的边上滑动，显然这四个点的每一组位置对应一个非正放的正方形(虽然正好在四个角上的是正放的)。

于是我们可以得出总方案数为sigma( i from 1 to min(n,m) ) i * ( n - i + 1 ) * ( m - i + 1 ) 。

这个东西可以O(n)计算。

对于正好有一个坏点的，我们考虑某个以某个个点P为角的正方形A，点P一定包含这个正方形A的最小正放正方形的角上或边上。

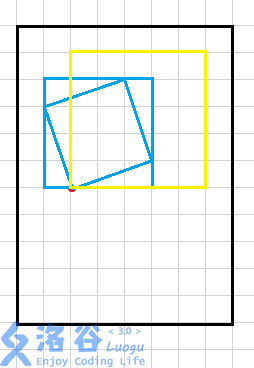
于是我们枚举这样的正方形和点P能在的位置数量就好了。

对于点P的状态，我们计算出它距离左边界的距离l，右边界距离r，上边界距离h。 然后我们令t=min(l+r,h)。

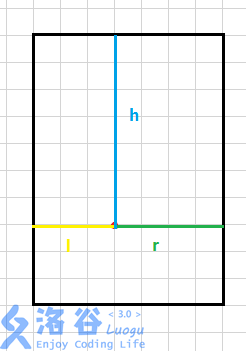
如果我们不考虑有一些位置不能取到的话，答案应该为t*(t+3)/2。

然而这样计算了一些不能取到的位置。当t>l时，我们多计算的位置数量为(t-l)*(t-l+1)/2。(手玩一下就明白了)

t>r时同理。这样我们就能O(k)计算出至少含一个坏点的方案数。

对于正好含两及以上个坏点的，我们枚举两个坏点，显然一个正方形给你两个点，他的位置就基本确定了。

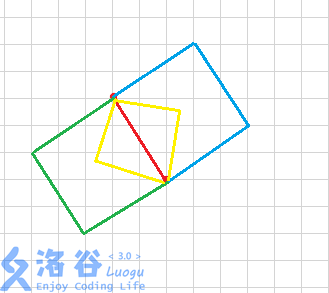
我们可以分类讨论三种情况，用向量计算出另外两个点应该在的位置。注意某些情况下以这两个点为对角线的正方形可能不在格点上。

然后对于含两个的，我们直接计算可行的正方形数；对于含三个的，我们当另外两个点有一个为坏点时计算；含四个的，我们当另外两个点均为坏点时计算。

显然含三个和含四个的我们算重了。所以应该分别除以C(3,2)和C(4,2)。

然后累加一下答案就好。 (然而计算垂直向量时没有加负号让我调了半天，老年选手身败名裂) 代码:

#include<cstdio>
#include<algorithm>
#include<tr1/unordered_set>
typedef long long int lli;
using namespace std;
using namespace tr1;
const int maxp=2e3+1e2;
const int mod=1e8+7;

struct Point {
    int x,y;
    friend bool operator < (const Point &a,const Point &b) {
        return a.x != b.x ? a.x < b.x : a.y < b.y;
    }
    friend Point operator - (const Point &a,const Point &b) {
        return (Point){a.x-b.x,a.y-b.y};
    }
    friend Point operator + (const Point &a,const Point &b) {
        return (Point){a.x+b.x,a.y+b.y};
    }
    friend Point operator * (const Point &a,const int &b) {
        return (Point){a.x*b,a.y*b};
    }
    friend Point operator / (const Point &a,const int &b) {
        return (Point){a.x/b,a.y/b};
    }
    inline Point swp() const {
        return (Point){y,-x};
    }
    inline bool candiv() const {
        return ( ! ( x & 1 ) ) && ( ! ( y & 1 ) );
    }
}pt[maxp];
unordered_set<lli> st;
int n,m,t;
lli ans,ini,sig,dou,tri,qua;

inline void insert(const Point &p) {
    lli h = (lli) p.x * ( m + 1 ) + p.y;
    st.insert(h);
}
inline bool inside(const Point &p) {
    return 0 <= p.x && p.x <= n && 0 <= p.y && p.y <= m;
}
inline bool legal(const Point &pa,const Point &pb) {
    return inside(pa) && inside(pb);
}
inline bool have(const Point &p) {
    lli h = (lli) p.x * ( m + 1 ) + p.y;
    return st.find(h) != st.end();
}
inline lli calcini(lli n,lli m) {
    lli ret = 0 , lim = min( n , m );
    for(lli i=1;i<=lim;i++) ret = ( ret + ( n - i + 1 ) % mod * ( m - i + 1 ) % mod * i % mod ) % mod;
    return ret;
}
inline lli calcedge(const lli &l,const lli &r,const lli &h) {
    lli t = min( l + r , h );
    if( !t ) return 0;
    lli ret = ( t * ( t + 3 ) >> 1 ) % mod;
    if( t > l ) ret -= ( ( t - l ) * ( t - l + 1 ) >> 1 ) % mod;
    if( t > r ) ret -= ( ( t - r ) * ( t - r + 1 ) >> 1 ) % mod;
    return ( ret % mod + mod ) % mod;
}
inline lli calcsingle(lli x,lli y) {
    const lli a = n - x , b = m - y , c = x , d = y;
    lli ret = ( calcedge(d,b,a) + calcedge(d,b,c) + calcedge(a,c,b) + calcedge(a,c,d) ) % mod;
    ret -= ( min(a,b) + min(b,c) + min(c,d) + min(d,a) ) % mod;
    return ( ret % mod + mod ) % mod;
}
inline lli calcdouble(const Point &a,const Point &b) {
    const Point delta = (a-b).swp();
    int ret = legal(a+delta,b+delta) + legal(a-delta,b-delta);
    const Point mid = a + b , pa = mid + delta , pb = mid - delta;
    if( pa.candiv() && pb.candiv() && legal(pa/2,pb/2) ) ++ret;
    return ret;
}
inline lli calctriple(const Point &a,const Point &b) {
    const Point delta = (a-b).swp();
    int ret = 0;
    if( legal(a+delta,b+delta) ) ret += have(a+delta) + have(b+delta);
    if( legal(a-delta,b-delta) ) ret += have(a-delta) + have(b-delta);
    const Point mid = a + b , pa = mid + delta , pb = mid - delta;
    if( pa.candiv() && pb.candiv() && legal(pa/2,pb/2) ) ret += have(pa/2) + have(pb/2);
    return ret;
}
inline lli calcquad(const Point &a,const Point &b) {
    const Point delta = (a-b).swp();
    int ret = 0;
    if( legal(a+delta,b+delta) ) ret += ( have(a+delta) && have(b+delta) );
    if( legal(a-delta,b-delta) ) ret += ( have(a-delta) && have(b-delta) );
    const Point mid = a + b , pa = mid + delta , pb = mid - delta;
    if( pa.candiv() && pb.candiv() && legal(pa/2,pb/2) ) ret += ( have(pa/2) && have(pb/2) );
    return ret;
}

int main() {
    scanf("%d%d%d",&n,&m,&t);
    for(int i=1;i<=t;i++) scanf("%d%d",&pt[i].x,&pt[i].y) , insert(pt[i]);
    ini = calcini(n,m);
    for(int i=1;i<=t;i++) sig += calcsingle(pt[i].x,pt[i].y);
    for(int i=1;i<=t;i++) for(int j=i+1;j<=t;j++) {
        dou += calcdouble(pt[i],pt[j]) , tri += calctriple(pt[i],pt[j]) , qua += calcquad(pt[i],pt[j]);
    }
    tri /= 3 , qua /= 6;
    ans = ( ( ini - sig + dou - tri + qua ) % mod + mod ) % mod;
    printf("%lld\n",ans);
    return 0;
}