自动搬运

查看原文

来自洛谷，原作者为

	seajupiter **

搬运于2025-08-24 21:47:07，当前版本为作者最后更新于2020-07-02 11:33:48，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

（不好意思麻烦管理员啦，以前没用过图床，结果这回写完就把图删掉了/笑哭）

算法：斯坦纳树+状压DP

此题题意很简单，就是要在图中选出一些边把给出的几个点集各子内部的点连通起来，问最小边权和。

看道题目就很容易想到斯坦纳树，但是注意：斯坦纳树是要求所有关键点联通，而此题只需要同一个类的关键点联通，不同类关键点连不连通都可以。那么就不能直接斯坦纳树了，该怎么做呢？

我们考虑一下斯坦纳树的状态设计，$f_{s, i}$ 表示 $s$ 集合内部的点都联通且根为 i 时的最小代价，是不是有启发呢？这道题棘手之处就在于你不知道哪些类会连在一棵树里，那么就可以一样状压 DP 啊！

我们把点的类别（频道）叫做”颜色“，设 $g_s$ 表示把 $s$ 集合内部的点构成斯坦纳树森林，且保证

• 若某一个点在 $s$ 中，则所有与它相同颜色均在 $s$ 中；

• 所有同颜色的点在同一棵斯坦纳树中；

很显然有转移：

$g_s=\min\limits_{s' \subseteq s}{\ g_{s'}+g_{s-s'}}$

设所有关建点构成的集合为 $all$ ，最后的答案就是 $g_{all}$

也许你可能有疑惑：这样合并不会重复算边吗？

的确不错，是会重复算边，但是不影响。因为如果我们把所有的情况考虑到了，由于边权非负，最后得到的最优答案一定时没有重复算边权的。

但是我认为此题难点不在这里，而是在 $g$ 数组的初始化（也可能是我太菜了），因此在这里把我写的过程犯的几个错误说一下，希望能帮到一些朋友 QAQ。

先赋 inf：

	memset(g, 0x3f, sizeof(g));

然后解决初值问题。

最开始，我是这么写的（求大佬不要嘲笑啊）：

	for(int i=1; i<=K; ++i) if(p[i]){
		int S=p[i];
		for(int j=1; j<=n; ++j)
			g[S]=min(g[S], f[S][j]);
//		print(S),cout<<g[S]<<endl;
	}

$p_i$ 表示颜色为 $i$ 的点构成的集合。

直接把每个类的点搞一棵斯坦纳树嘛，之后不就可以合并了？

然而错的很离谱（话说这题数据是真的水，到后面你就知道了）……

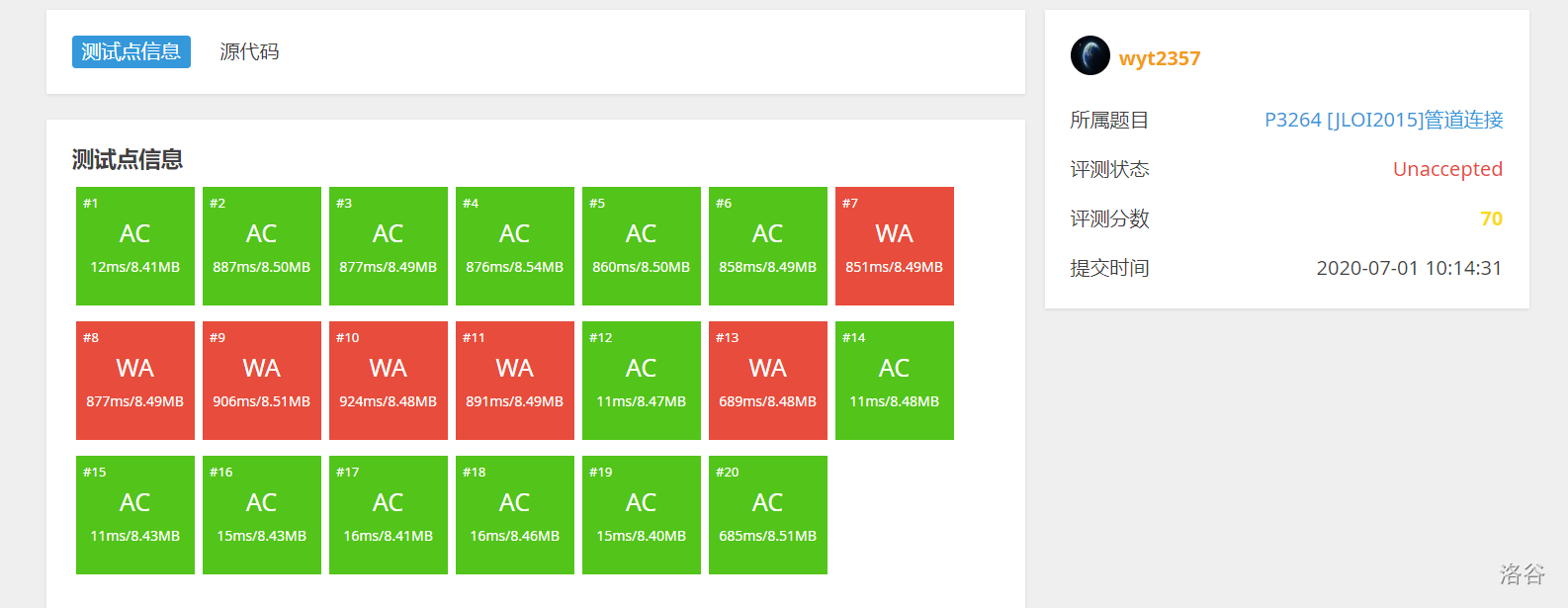
为什么？因为完全可以把几类点放到一棵树里头啊！否则可能后面 DP 最小值就可能会得到重复算边代价的答案，导致答案偏大。

那么，改一下就好了嘛：

for(int S=1; S<(1<<K); ++S){
	work(S);
	for(int i=1; i<=K; ++i) if(S&p[i]==p[i]){
		for(int j=1; j<=n; ++j)
			g[S]=min(g[S], f[S][j]);
		break;
	}
}

然而错的更离谱！要注意到，&的优先级是低于==的！ 所以这样根本不是在判断是否为子集！

然而居然~

好的赶快把这里改过来，以后要记得加括号，防止优先级问题。

改成了这样：

	for(int S=1; S<(1<<K); ++S){
		work(S);
		for(int i=1; i<=K; ++i) if(p[i]&&(S&p[i])==p[i]){
			for(int j=1; j<=n; ++j)
				g[S]=min(g[S], f[S][j]);
			break;
		}
	}

结果~

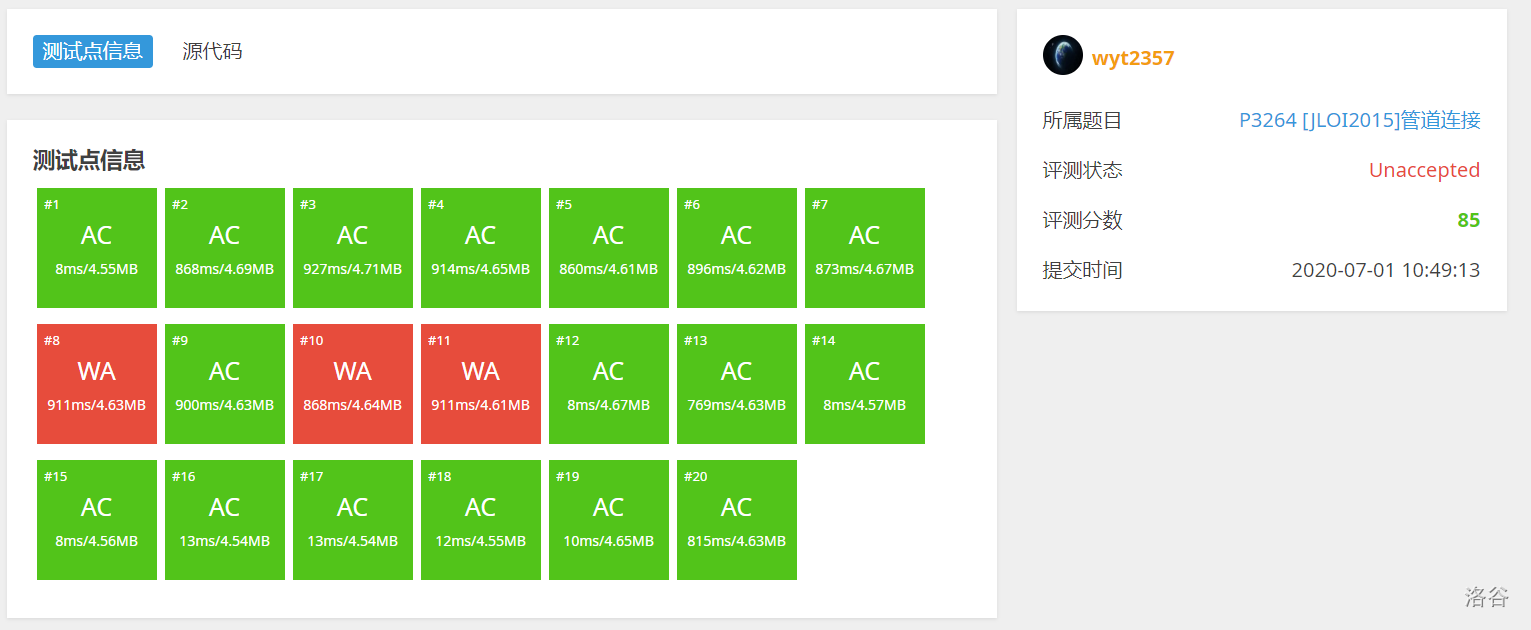
噫，怎么还是WA，有毒啊QAQ~

再仔细想一想，肯定还是状压DP部分的问题（斯坦纳树我是先过了模板的）。

观察评测结果，发现这次结果似乎偏小了！那么一定是不合法的状态更新了答案，也就是说，与上面状态限制中的两条发生了违背。为什么会这样呢？

仔细考虑这个判断，我们的思路是：只要这个集合包含了某一类点的全部，就可以建成一棵斯坦纳树。 漏洞在哪里？举个例子，如果这个集合虽然包含了所有”红色点“，但是包含了一部分”黄色点“的话，其实是不满足我们列出的两个条件的，因为有黄色点在这个集合中，然而并非所有黄色点都在这个集合中，也并非所有黄色点都在一棵斯坦纳树中。

形式化地讲，在初始化的时候（把初始化集合的点全部建到一棵树里头去），一个集合 $s$ 合法，当且仅当：

对于任何一种颜色，所有为此颜色的点要么全部在 $s$ 中，要么全部不在 $s$ 中。

弄明白了这个，总算可以写出正确程序了：

	for(int S=1; S<(1<<K); ++S){
		work(S);
		bool flag=true;
		for(int i=1; i<=K; ++i) if(p[i])
			if((S&p[i])!=p[i]&&(S&p[i])!=0) flag=false;
		if(flag) for(int i=1; i<=n; ++i)
			g[S]=min(g[S], f[S][i]);
	}

下面给出完整 AC 代码：

#include <bits/stdc++.h>
using namespace std;
inline void read(int &x){
	char c=getchar();x=0;
	while(!isdigit(c))c=getchar();
	while(isdigit(c))x=x*10+c-'0',c=getchar();
}
const int N=1005, M=3005, V=N, E=M<<1, NUM=15, SZ=1<<10|5, inf=0x3f3f3f3f;
int n, m, K, key[NUM], col[NUM], p[NUM], f[SZ][N], ans, g[SZ];
int e, head[V], to[E], val[E], nxt[E];
inline void add(int u, int v, int w){
	to[++e]=v, val[e]=w;
	nxt[e]=head[u], head[u]=e;
}
inline void spfa(int *f){
	static bool inq[N];
	static queue<int> q;
	for(int i=1; i<=n; ++i) if(f[i]<inf)
		q.push(i), inq[i]=true;
	while(!q.empty()){
		int u=q.front(); q.pop(), inq[u]=false;
		for(int i=head[u]; i; i=nxt[i]){
			int v=to[i], w=val[i];
			if(f[v]>f[u]+w){
				f[v]=f[u]+w;
				if(!inq[v]) q.push(v), inq[v]=true;
			}
		}
	}
}
inline void work(int S){
	for(int s=(S-1)&S; s; s=(s-1)&S)
		for(int i=1; i<=n; ++i)
			f[S][i]=min(f[S][i], f[s][i]+f[S^s][i]);
	spfa(f[S]);
}
int main(){
	read(n);read(m);read(K);
	for(int i=1, u, v, w; i<=m; ++i){
		read(u);read(v);read(w);
		add(u, v, w), add(v, u, w);
	}
	memset(f, 0x3f, sizeof(f));
	memset(g, 0x3f, sizeof(g));
	for(int i=1; i<=K; ++i){
		read(col[i]);read(key[i]);
		f[1<<(i-1)][key[i]]=0;
		p[col[i]]|=(1<<(i-1));
	}
	for(int S=1; S<(1<<K); ++S){
		work(S);
		bool flag=true;
		for(int i=1; i<=K; ++i) if(p[i])
			if((S&p[i])!=p[i]&&(S&p[i])!=0) flag=false;
		if(flag) for(int i=1; i<=n; ++i)
			g[S]=min(g[S], f[S][i]);
	}
	for(int S=1; S<(1<<K); ++S)
		for(int s=(S-1)&S; s; s=(s-1)&S)
			g[S]=min(g[S], g[s]+g[S^s]);
	printf("%d\n", g[(1<<K)-1]);
	return 0;
}

这道题不能算是难题，但是写的时候还是要很注意细节，我就是因为这个初始化被坑了好久。所以建议大家在写 DP 的时候，要把状态的定义和转移条件等清晰地列出来，并根据这个考察代码的逻辑是否正确。希望这篇题解能帮到大家！（也希望管理员放通过一下，谢谢啦！）