自动搬运

查看原文

来自洛谷，原作者为

	TKXZ133 竭诚则胡越为一体，傲物则骨肉为行路

搬运于2025-08-24 21:47:05，当前版本为作者最后更新于2023-06-01 21:56:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

镜面通道

题目大意

在一个二维平面内，给出一个镜面通道和若干个镜面元件，每个元件可能是圆形或矩形。求出为了能够使光从通道左边通过通道到达右边，至少需要拿走的元件个数。

思路分析

首先，存在一个结论：如果通道中存在从左边到右边的路径，那么光就能通过。

证明一下：当通道中存在从左边到右边的路径时，我们不妨将通道竖直放置，令左边朝上，向通道中注水，那么水一定能从下方流出。考虑水恰好流出时，即流出的水形成“水线”时，将通道的剩余部分填满，那么光一定可以沿顺着水的方向通过，所以在剩余部分没有填满的情况下光也能通过。

那么现在的问题就变成了，至少需要拿走多少元件可以使得通道中存在从左到右的路径，而这等价于通道的上下边界无法通过元件连通。

我们发现，上下边界的连通性与元件的形状，大小均无关，只与元件之间是否接触有关。那么我们可以将元件抽象成点，点与点之间存在边当且仅当两个点代表的元件接触，这样就形成了一张图。

我们同时也可以将上下边界抽象成点加入图，连边方式与元件类似，即如果存在元件与边界相接触，那么将该元件代表的点和边界代表的点连边。

那么问题就转化为了，至少需要删除多少个点，可以使得上下边界代表的两点不连通。

这显然是一个最小割问题，可以通过网络流解决。

建图方式比较简单，将点拆成入点和出点，出入点之间连边权为 $1$ 的边，将上下边界代表的点设为源点和汇点，点与点之间，点与边界之间连边权为 $+\infty$ 的边即可。

现在考虑如何判断两个元件之间接触：

• 圆和圆

直接计算两圆心的距离是否小于等于半径之和即可。

• 矩形和矩形

枚举两个矩形的四个顶点是否在另一矩形内即可？

考虑如下情况：

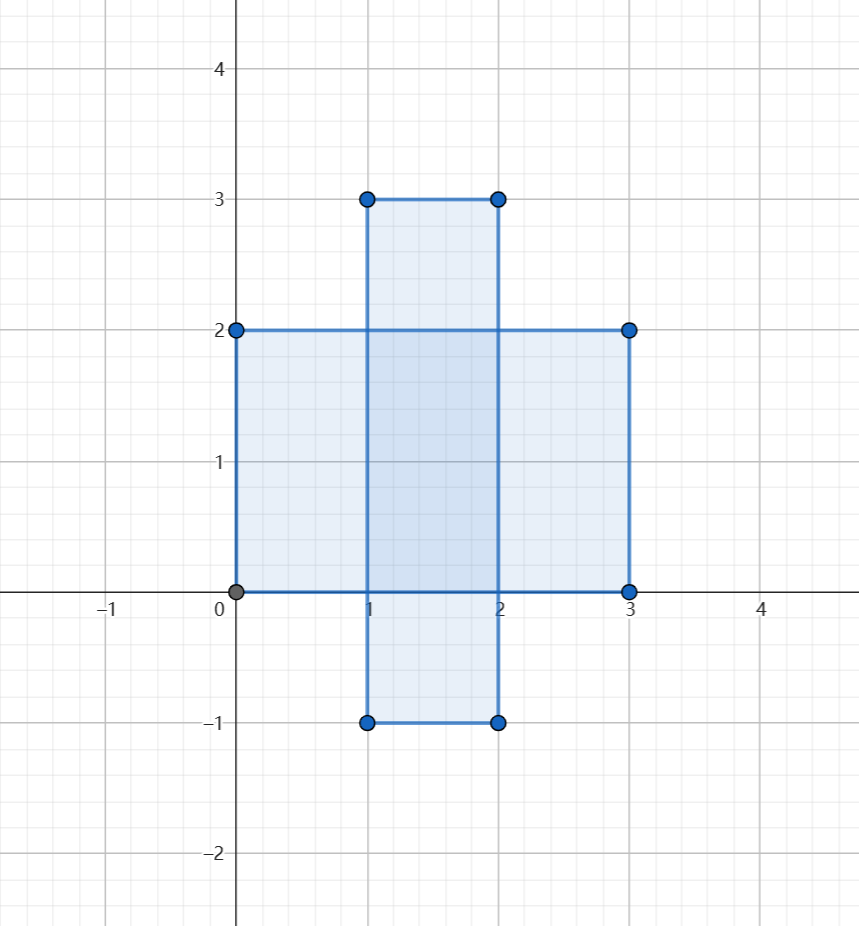
因此还需逐一判断边是否相交。

• 圆和矩形

可以转化成点是否在一个圆角矩形内，将圆角矩形拆成四个圆和两个矩形，将点视为半径为 $0$ 的圆用上面的方法做即可。

代码

#include <iostream>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <queue>

using namespace std;
const int M=330,N=220000;
#define eps 1e-6
#define inf 0x3f3f3f3f

int n,S,T,idx=1,op;
double in1,in2,in3,in4,cx,cy;
int to[N],nxt[N],head[N],w[N];
int cur[N],d[N];

void add(int u,int v,int c){
    idx++;to[idx]=v;nxt[idx]=head[u];head[u]=idx;w[idx]=c;
    idx++;to[idx]=u;nxt[idx]=head[v];head[v]=idx;w[idx]=0;
}

queue <int> q;

bool bfs(){
    memset(d,-1,sizeof d);
    while(!q.empty()) q.pop();
    cur[S]=head[S];
    q.push(S);d[S]=0;
    while(!q.empty()){
        int now=q.front();q.pop();
        for(int i=head[now];i;i=nxt[i]){
            int v=to[i];
            if(~d[v]||!w[i]) continue;
            d[v]=d[now]+1;
            cur[v]=head[v];
            if(v==T) return 1;
            q.push(v);
        }
    }
    return 0;
}

int dfs(int s,int lim){
    if(s==T) return lim;
    int flow=0;
    for(int i=cur[s];i&&flow<lim;i=nxt[i]){
        int v=to[i];cur[s]=i;
        if(d[v]!=d[s]+1||!w[i]) continue;
        int t=dfs(v,min(w[i],lim-flow));
        if(!t) d[v]=-1;
        w[i]-=t;w[i^1]+=t;flow+=t;
    }
    return flow;
}

int dinic(){//dinic 板子
    int ans=0,flow=0;
    while(bfs()) while(flow=dfs(S,inf)) ans+=flow;
    return ans;
}

struct Node{
    int type;//1代表圆，2代表矩形，3表示线段
    double x1,y1,x2,y2,r;
}a[M];

double dis_two_points(double x1,double y1,double x2,double y2){//计算两点距离
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}

bool Point_Rec(double x1,double y1,Node a){//判断点是否在矩形内
    return (x1>a.x1-eps)&&(x1<a.x2+eps)&&(y1>a.y1-eps)&&(y1<a.y2+eps);
}

bool Lin_Int(Node a,Node b){//判断特定直线是否相交
    return (a.x1<=b.x1&&b.x1<=a.x2)&&(b.y1<=a.y1&&a.y1<=b.y2);
}

bool Cyc_Int(Node a,Node b){//判断圆是否相交
    return dis_two_points(a.x1,a.y1,b.x1,b.y1)<a.r+b.r+eps;
}

bool Rec_Int(Node a,Node b){//判断两个矩形是否相交
    bool res1=Point_Rec(a.x1,a.y1,b);
    bool res2=Point_Rec(a.x2,a.y2,b);
    bool res3=Point_Rec(a.x1,a.y2,b);
    bool res4=Point_Rec(a.x2,a.y1,b);//判点
    Node line1=Node{3,a.x1,a.y1,a.x2,a.y1};
    Node line2=Node{3,a.x1,a.y1,a.x1,a.y2};
    Node line3=Node{3,a.x2,a.y1,a.x2,a.y2};
    Node line4=Node{3,a.x1,a.y2,a.x2,a.y2};
    Node line5=Node{3,b.x1,b.y1,b.x2,b.y1};
    Node line6=Node{3,b.x1,b.y1,b.x1,b.y2};
    Node line7=Node{3,b.x2,b.y1,b.x2,b.y2};
    Node line8=Node{3,b.x1,b.y2,b.x2,b.y2};//两个矩形八条线
    bool res5=Lin_Int(line1,line6)||Lin_Int(line1,line7);
    bool res6=Lin_Int(line2,line5)||Lin_Int(line2,line8);
    bool res7=Lin_Int(line3,line5)||Lin_Int(line3,line8);
    bool res8=Lin_Int(line4,line6)||Lin_Int(line4,line8);//线是否相交
    return res1||res2||res3||res4||res5||res6||res7||res8;
}

bool check(Node a,Node b){
    if(a.type==1&&b.type==1) return Cyc_Int(a,b);
    if(a.type==2&&b.type==2) return Rec_Int(a,b)||Rec_Int(b,a);//考虑一个矩形在另一个矩形内的情况
    if(a.type!=b.type){
        if(a.type==2) swap(a,b);
        Node point=Node{1,a.x1,a.y1,0,0,0};
        bool res1=Cyc_Int(point,Node{1,b.x1,b.y1,0,0,a.r});
        bool res2=Cyc_Int(point,Node{1,b.x2,b.y2,0,0,a.r});
        bool res3=Cyc_Int(point,Node{1,b.x1,b.y2,0,0,a.r});
        bool res4=Cyc_Int(point,Node{1,b.x2,b.y1,0,0,a.r});//视为四个圆和两个矩形
        bool res5=Point_Rec(a.x1,a.y1,Node{2,b.x1-a.r,b.y1,b.x2+a.r,b.y2});
        bool res6=Point_Rec(a.x1,a.y1,Node{2,b.x1,b.y1-a.r,b.x2,b.y2+a.r});
        return res1||res2||res3||res4||res5||res6;
    }
    return 0;
}

int main(){
    scanf("%lf%lf%d",&cx,&cy,&n);
    for(int i=1;i<=n;i++){
        scanf("%d%lf%lf%lf",&op,&in1,&in2,&in3);
        if(op==2) scanf("%lf",&in4);
        if(op==1) a[i]=Node{1,in1,in2,0,0,in3};
        if(op==2) a[i]=Node{2,in1,in2,in3,in4};
    }
    S=N-5;T=N-6;
    a[n+1]=Node{2,-inf,cy,inf,inf};//上下边界可以当作两个无穷大的矩形
    a[n+2]=Node{2,-inf,-inf,inf,0};
    for(int i=1;i<=n;i++){
        if(check(a[n+1],a[i])) add(S,2*i-1,inf);
        if(check(a[n+2],a[i])) add(2*i,T,inf);
        add(2*i-1,2*i,1);//入点和出点
        for(int j=i+1;j<=n;j++)//暴力加边即可
            if(check(a[i],a[j])){
                add(2*i,2*j-1,inf);
                add(2*j,2*i-1,inf);
            }
    }  
    cout<<dinic()<<'\n'; 
    return 0;
}