自动搬运

查看原文

来自洛谷，原作者为

	dzz1537568241 愿你的所有努力，都不负韶华

搬运于2025-08-24 21:47:03，当前版本为作者最后更新于2019-10-06 18:22:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

树上差分

本题解有：

1. 差分的思想原理 + 做 差分 题的小技巧

2. 树上差分

要看懂这篇题解 .... 你必须熟练掌握 ：

1. LCA

2. 差分

• LCA的题目可以做：

  P3379 【模板】最近公共祖先（LCA）

  P1351联合权值

• 至于差分，他实在是太重要了，我相信各位都掌握了，如果你不会我建议打回普及组重造

---

一：差分的思想原理

先来大致分析一下我们本题要干什么

1. 找到两个节点的最近公共祖先

2. 处于到最近公共祖先的路径上的所有节点 均 + 1

考虑到本题的数据量，遍历最近公共祖先的路径，然后逐个加 1，显然不可能

与区间加值有关系的：

• 线段树

• 差分

• 树状数组

线段树 和 树状数组用于数轴上的处理比较多，而树上的路径是无法表示成一个个区间

这里差分的优点就非常明显了：

• 算法复杂度超低

• 适用于一切 连续的 “线段”

这里所谓的线段可以是一段连续的区间，也可以是路径

唯一的问题是怎么差分？

我们先暂时抛开这道题目，想象一下出一条链表...

把1 -> 5这条路径上的值全体加1

现在来处理差分数组

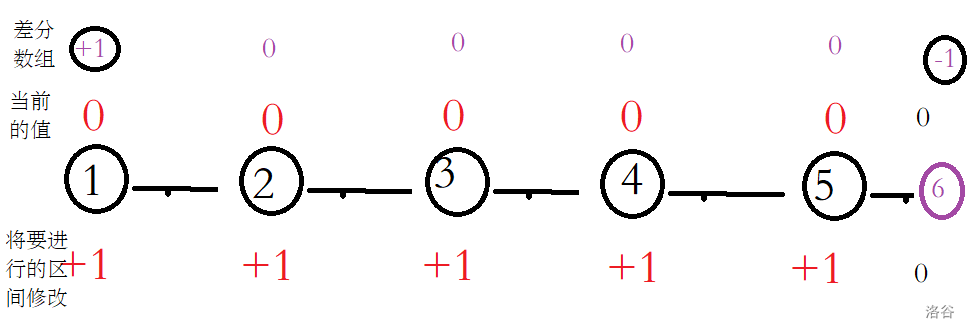
可以很清楚的看到，1号节点的值被增加1，在 6号节点的值被减去1

正确性很好说明：差分数组的的定义：a[ i ] = a[ i - 1 ] + 差分数组[ i ],

由于区间[1, 5]区间内，两个数之间的相对大小不会改变，改变的只是a[1]相对于a[0]的大小和a[5]相对于a[6]的大小，因此只需把a[1] + 1，a[6] - 1即可；

可以总结出差分的思想方法：

如果有一个区间内的权值发生相同的改变的时候，我们可以采用差分的思想方法

而差分的思想方法在于不直接改变区间内的值，而是改变区间[ L , r ] 对于 区间 [ 0, L - 1 ] & 区间[ r + 1, R]的 相对大小关系

总结出一点：

差分就是相对改变 ！

差分就是相对改变！！

差分就是相对改变！！！

只要我们能找出区间和区间之间相对改变的关系，一切均能被差分轻松的解决

另注：（防止接下来有人会看的云里雾里的）

接下来所有“子节点”指“ 直系子节点”！！！！

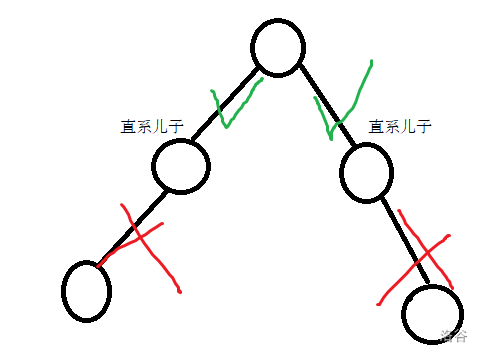
直系子节点指的是和父节点有一条边直接相连的子节点

二：树上差分

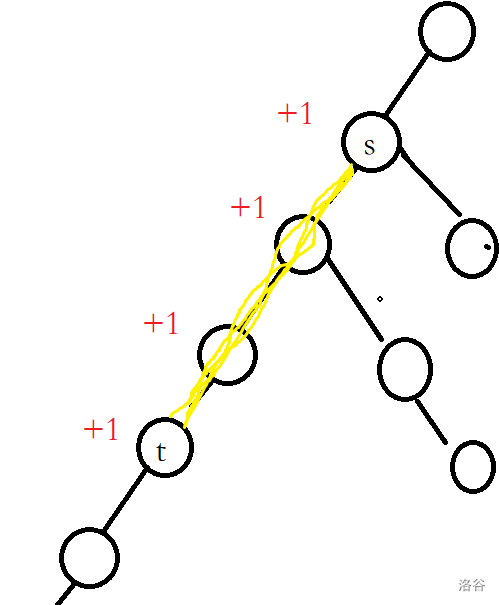
类比刚才的差分，

如果把s -> t的路径上的所有节点的权值都加上 w，

我们假定一个父节点u = 其所有的子节点 + 他本身的差分数组

写出伪代码：

//chafen[ maxn ]：差分数组，定义 当前节点 与其子树的总和之差 
//num[ maxn ]: 当前节点的权值 

int chafen[maxn], a[maxn];

num[u] += chafen[u];//加上差分数组 

//加上子树的总和 
for(遍历与 u 相连的每一个子节点 v){
	num[u] += num[v]; 
} 

我们要处理的相对改变有以下几种可能：

1. s -> t路径上的点与他们的子节点 的相对改变

2. s 与 s父节点 的相对改变

3. t 与 t子节点 的相对改变

• 来看 s -> t 路径上的点（不包括 t） 和他们的子节点的总和 的相对改变

有改变吗？

A) 当然是有的

B) 和 自己子节点的和 发生相对改变...？嗯和 单个子节点 确实是有相对改变，但是和他的子节点的和应该是没有吧。

如果你选 A）你可以看一眼 B）

如果你选 B）那恭喜你选对了。

差分数组存储该节点相对于其子节点的总和发生的相对改变，在s->t路径上所有点的子节点 均和 他们自己发生了同样的改变，因此相对改变为0

• 再来看 t 和 t 子节点总和 的相对改变

显然是有的，大小也很好看出，t 比 其子节点总和高出了w, 因此在处理差分的时候只需要把 t 的差分数组值 + w 即可

• 最后是 s 与 s父节点的相对改变

s的值增了 w， s的父节点相对于其子树和 小了s，只需要把 s的父节点的差分数组值 - w即可

这样把s -> t路径上的值均加w的树上差分的伪代码就能写出来了

int chafen[maxn], a[maxn];

num[u] += chafen[u];//加上差分数组 

//把s->t路径上所有点均加w,
chafen[t] += w;
chafen[s的父节点] -= w; 

//差分数组处理 
//加上子树的总和 
for(遍历与 u 相连的每一个子节点 v){
	num[u] += num[v]; 
}  

（其实和普通的差分并没有什么区别）

三：lca上的差分

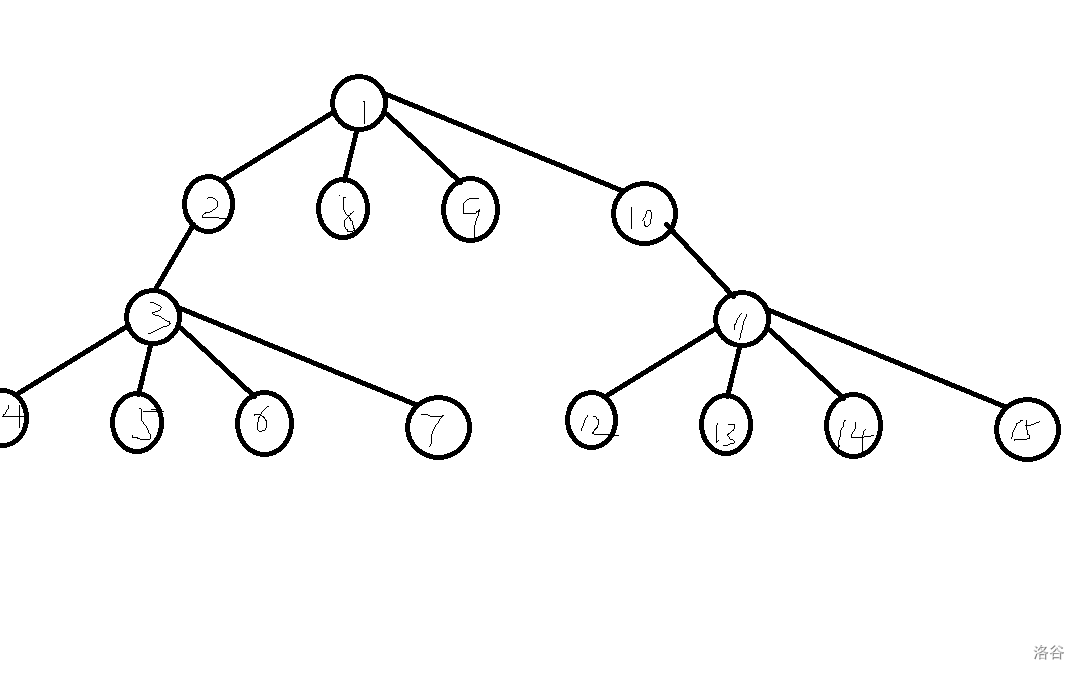
如上图所示 （我随便画的树）

lca的差分在原来的基础上稍微加了一丁点东西，我觉得不需要我仔细的讲，因为如果要是刚才的树上差分学会了lca上的差分还是不会你肯定没动脑子

假设 把4和5的lca路径上的点权值均 + 1

可以把这个问题拆成两个问题求解：

1. 4 -> 最近公共祖先 路径上的点+1

2. 5 -> 最近公共祖先 路径上的点+1

最后由于最近公共祖先被多加了一次，因此 lca(4,5)的差分数组应该 - 1，他的父亲节点的差分数组应该+ 1

给出所有的代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

const int maxn = 300050;
const int maxm = maxn << 1;
int N, M;
int a[maxn], t1, t2;
int head[maxn], cnt;

struct Edge{
	int u, v, next;
}edge[maxm];

inline void addedge(int u, int v){
	edge[++cnt].u = u;
	edge[cnt].v = v;
	edge[cnt].next = head[u];
	head[u] = cnt;
}

int fa[maxn][31], dep[maxn];

void dfs(int u, int faa){
	fa[u][0] = faa, dep[u] = dep[faa] + 1;
	for(int i = 1; i <= 30; i++){
		fa[u][i] = fa[ fa[u][i - 1] ][i - 1];
	}
	for(int i = head[u]; i ; i = edge[i].next){
		int v = edge[i].v;
		if(v == faa)continue;
		dfs(v, u);
	}
} 

inline int lca(int x, int y){
	if(dep[x] < dep[y])swap(x,y);
	for(int i = 30; i >= 0; i--){
		if(dep[ fa[x][i] ] >= dep[y]) x = fa[x][i];
	}
	if(x == y)return x;
	for(int i = 30; i >= 0; i--){
		if(fa[x][i] != fa[y][i]){
			x = fa[x][i], y = fa[y][i];
		}
	}
	return fa[x][0];
}

int num[maxn];

int answer(int u, int faa){
	for(int i = head[u]; i ; i = edge[i].next){
		int v = edge[i].v;
		if(v == faa)continue;
		answer(v, u);
		num[u] += num[v];
	}
}
int main(){
	cin>>N;
	for(int i = 1; i <= N; i++){
		cin>> a[i];
	}
	for(int i = 1; i < N; i++){
		cin>> t1>> t2;
		addedge(t1, t2);
		addedge(t2, t1);
	}
	dfs(1, 0);
	for(int i = 1; i <= N - 1; i++){
		int u = a[i], v = a[i + 1];
		int t = lca(u, v);
		num[ fa[t][0] ]	-= 1;
		num[ t ] -= 1;
		num[ u ] += 1;
		num[ v ] += 1;
	}
	answer(1,0);
	for(int i = 2; i <= N; i++){
		num[a[i]]--;
	}
	for(int i = 1; i <= N; i++){
		cout<<num[i]<<endl;
	}
}

学农的时候还要写个题解求个赞应该不过分吧？