1 条题解
-
0
自动搬运
来自洛谷,原作者为

MCAdam
寻芳不觉醉流霞,倚树沉眠日已斜搬运于
2025-08-24 21:46:46,当前版本为作者最后更新于2020-05-01 18:23:05,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
首先考虑暴力:
我们要计算每一个点离它最近的议事点,这个可以通过两遍完成
1、计算当前点到它子树中最近的议事点,先递归的儿子再计算
2、此时根节点就保存了它需要的答案,我们用父亲节点去更新儿子,更新完后再递归
inline void dfs1(int p,int fa) { dp[p]=INF;//dp表示最短距离,g表示编号 for(register int i=fir[p];i;i=e[i].nxt) { int q=e[i].to; if(q==fa) continue; dfs1(q,p);//用儿子更新自己 if(dp[q]+1<dp[p]) dp[p]=dp[q]+1,g[p]=g[q]; else if(dp[q]+1==dp[p]) g[p]=min(g[p],g[q]); } if(vis[p]) dp[p]=0,g[p]=p; vis[p]=0; } inline void dfs2(int p,int fa) { for(register int i=fir[p];i;i=e[i].nxt) { int q=e[i].to; if(q==fa) continue;//用自己更新儿子 if(dp[p]+1<dp[q]) dp[q]=dp[p]+1,g[q]=g[p]; else if(dp[p]+1==dp[q]) g[q]=min(g[q],g[p]); dfs2(q,p); } }看到有,套路地建一棵虚树
对于虚树上的点(议事点和它们的),议事点答案当然是自己本身,对于点,就像上面暴力一样遍历整棵虚树就行了。注意此时,虚树上的节点并不是连续的,所以两个点之间的距离并不是,要预处理每个点在原树上的深度
那怎么计算非虚树上的节点呢?
第一种情况:
原树上一个点,对于它的某个儿子,如果这个子树中没有议事点,那么整棵子树肯定都是从离最近的议事点走过来的
第二种情况:
原树上一条链,两端都是议事点,这一条链各一半属于两个议事点
对应到虚树上就是:
1、一个虚树点,如果它在在原树上的某个儿子,整棵子树都没有议事点,那么这颗子树的大小就能贡献到
2、对于虚树上的一条边,它两端和(即使是点也行,因为点我们已经处理好了)。虚树上的这一条边对应的是原树的一条链,我们要找到这条链上的分界点。这个直接由倍增就可以了。
具体实现:
1、对于虚树上的一个点,它的一个儿子,我们要计算在原树中的儿子(注意区分),子树中没有议事点。因为我们不能遍历原树,只能遍历虚树,但因为虚树上的儿子节点对应上来的肯定是不用贡献的,那我们就用减去对应上来的儿子的就是我们要的了。具体写的时候可以先全部减掉再加回来。
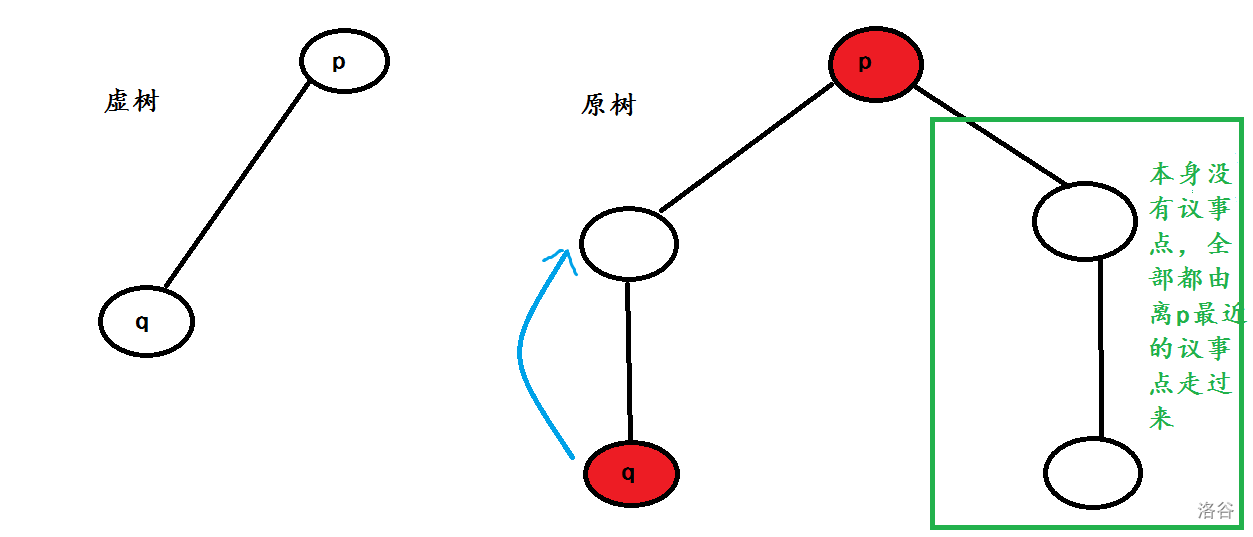
2、原树上的链。虚树上的两个点和(是虚树上的儿子)对应到原树上的链,在这上面倍增找到分割点,然后计算贡献。注意虚树上的这一条边,对应到原树上是一条链并且挂着许多的子树。子树的贡献也是要算上的。注意这一步是只计算链上且不包括两端的情况,所以同样要找到在原树上的儿子。
举个栗子(样例第三个再加一个点):
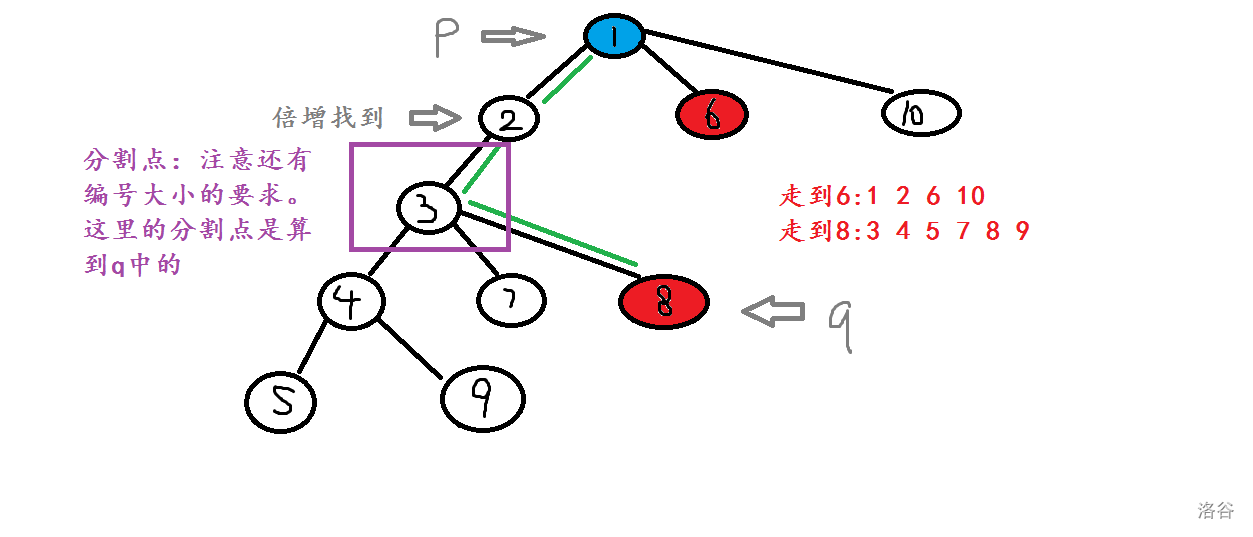
我们倍增找到对应上来的的儿子(2),以及分割点(3),那么此时都算到的答案中,也就是;此时算到中,也就是
#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <algorithm> using namespace std; const int N=3e5+10,INF=1e9+10; int n,m,top,cnt; int dep[N],f[N][20],dfn[N],size[N],lg2[N],sta[N],pnt[N],vis[N],g[N],dp[N],ans[N],tmp[N]; struct graph { int tot; int fir[N],to[2*N],nxt[2*N]; graph(){ tot=0; memset(fir,0,sizeof(fir)); } inline void add(int x,int y) { to[++tot]=y; nxt[tot]=fir[x]; fir[x]=tot; to[++tot]=x; nxt[tot]=fir[y]; fir[y]=tot; } }e1,e2; inline void dfs(int p)//预处理dfn,dep,size { dfn[p]=++cnt,size[p]=1; for(register int i=e1.fir[p];i;i=e1.nxt[i]) { int q=e1.to[i]; if(q==f[p][0]) continue; dep[q]=dep[p]+1,f[q][0]=p; for(register int j=1;j<=lg2[dep[q]]+1;j++) f[q][j]=f[f[q][j-1]][j-1]; dfs(q); size[p]+=size[q]; } } inline int get_lca(int x,int y)//找lca { if(dep[x]<dep[y]) swap(x,y); for(register int i=lg2[dep[x]];i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i]; if(x==y) return x; for(register int i=lg2[dep[x]];i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } inline bool cmp(int a,int b) { return dfn[a]<dfn[b]; } inline void build(int p)//建立虚树 { if(top==0){ sta[top=1]=p; return; } int lca=get_lca(sta[top],p); while(top>1&&dep[lca]<dep[sta[top-1]]) e2.add(sta[top-1],sta[top]),top--; if(dep[lca]<dep[sta[top]]) e2.add(lca,sta[top--]); if(top==0||sta[top]!=lca) sta[++top]=lca; sta[++top]=p; } inline void cal(int x,int y) { int p=y,q=y; for(register int i=lg2[dep[p]];i>=0;i--) if(dep[f[p][i]]>dep[x]) p=f[p][i]; ans[g[x]]-=size[p];//跳到y在原树上对应的x的儿子 for(register int i=lg2[dep[q]];i>=0;i--) { int llen=dep[y]-dep[f[q][i]]+dp[y],rlen=dep[f[q][i]]-dep[x]+dp[x]; if(dep[f[q][i]]>dep[x]&&(llen<rlen||(llen==rlen&&g[y]<g[x]))) q=f[q][i];//倍增找到分割点 } ans[g[y]]+=size[q]-size[y],ans[g[x]]+=size[p]-size[q];//注意这里要加的是size,因为虚树路径上会有子树 } inline void dfs1(int p,int fa) { dp[p]=INF; for(register int i=e2.fir[p];i;i=e2.nxt[i]) { int q=e2.to[i]; if(q==fa) continue; dfs1(q,p); int dis=dep[q]-dep[p];//注意这里,虚树上的节点并不是连续的 if(dp[q]+dis<dp[p]) dp[p]=dp[q]+dis,g[p]=g[q]; else if(dp[q]+dis==dp[p]) g[p]=min(g[p],g[q]); } if(vis[p]) dp[p]=0,g[p]=p; } inline void dfs2(int p,int fa) { for(register int i=e2.fir[p];i;i=e2.nxt[i]) { int q=e2.to[i]; if(q==fa) continue; int dis=dep[q]-dep[p]; if(dp[p]+dis<dp[q]) dp[q]=dp[p]+dis,g[q]=g[p]; else if(dp[p]+dis==dp[q]) g[q]=min(g[q],g[p]); cal(p,q); dfs2(q,p); } ans[g[p]]+=size[p];//注意这里,还要加上自己 vis[p]=e2.fir[p]=0; } int main() { lg2[1]=0; for(register int i=1;i<=3e5;i++) lg2[i]=lg2[i>>1]+1; int a,b,T; scanf("%d",&n); for(register int i=1;i<n;i++) { scanf("%d%d",&a,&b); e1.add(a,b); } dep[1]=1,dfs(1); scanf("%d",&T); while(T--) { int flag=1; top=e2.tot=0; scanf("%d",&m); for(register int i=1;i<=m;i++) scanf("%d",&pnt[i]),vis[pnt[i]]=1,ans[pnt[i]]=0; if(!vis[1]) pnt[++m]=1,flag=0; for(register int i=1;i<=m;i++) tmp[i]=pnt[i]; sort(pnt+1,pnt+m+1,cmp); for(register int i=1;i<=m;i++) build(pnt[i]); if(top) while(--top) e2.add(sta[top],sta[top+1]); dfs1(1,0),dfs2(1,0); for(register int i=1;i<=m;i++) if(tmp[i]!=1||flag) printf("%d ",ans[tmp[i]]);//注意判断1 printf("\n"); } return 0; }
- 1
信息
- ID
- 2306
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
