自动搬运

查看原文

来自洛谷，原作者为

	dengyaotriangle 我弱弱 您强强 嘤嘤嘤

搬运于2025-08-24 21:46:42，当前版本为作者最后更新于2021-05-06 22:25:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

注意：本文不是题解，而是正确性证明。

之前想过这个问题，看到确实有很多人像我一样的对正确性有疑问，就写一个详细的证明吧。

大多数本题解法给出了这样一个建图方式：建一条条链，具体，令 $(a,b)$ 为第 $a$ 条链第 $b$ 个点，建有向边：

1. $((a,b),(a,b+1),cost_{a,b})$
2. $(S,(a,1),\infty)$
3. $((a,m),T,\infty)$
4. $\forall x,y,z$ ，$x,y$ 相邻，$((x,z),(y,z-D),\infty)$

跑最小割，令第 $a$ 个点选了第 $b$ 个位置表现为割了边 $((a,b),(a,b+1))$，那么由于第 4 类边，一组合法的割必然满足 $|a_i-a_j|\leq D$，所以最小割就是答案。

注意到了啥？不加证明的声称了一条链最多割一条边。 为啥是对的？

1. 我们改个建图吧！

加第五类边： $((a,b),(a,b-1),\infty)$ 即可。显然，在一条链只割一条边的情况下，加了这条边后原来的割依然是割。

注意到这也是题目 P6054 的处理方式。

那道题的限制的种类更加丰富：给 $n$ 个变量 $a_i$，第 $i$ 个选 $j$ 代价 $c_{i,j}$ 且有若干个 $a_{v_i}\geq a_{u_i}+k_i$ 的限制。

其实，那这道题中，若不存在我们新加的第五类边，则真的有可能最优方案割了两条边。

为啥是对的，首先考虑一个引理：

引理：在割去最小割后，最小割的割边 $(u,v)$ 必须满足 $S\to u,v\to T$，其中 $\to$ 表示可以到达。

证：若 $S\to u$ ，$v\to T$ 任意一个不成立，不割这条边一定还是个割，且更优。

接下来就简单了，假设最小割有一条链，上面被割了$\geq2$ 条边，那么考虑相邻的两个割边，由于引理，第一个割边右边可以到 $T$ 、第二个左边可以到 $S$ ，那么由于有第五类边，那么无论怎样，$S\to T$，与是个割矛盾。

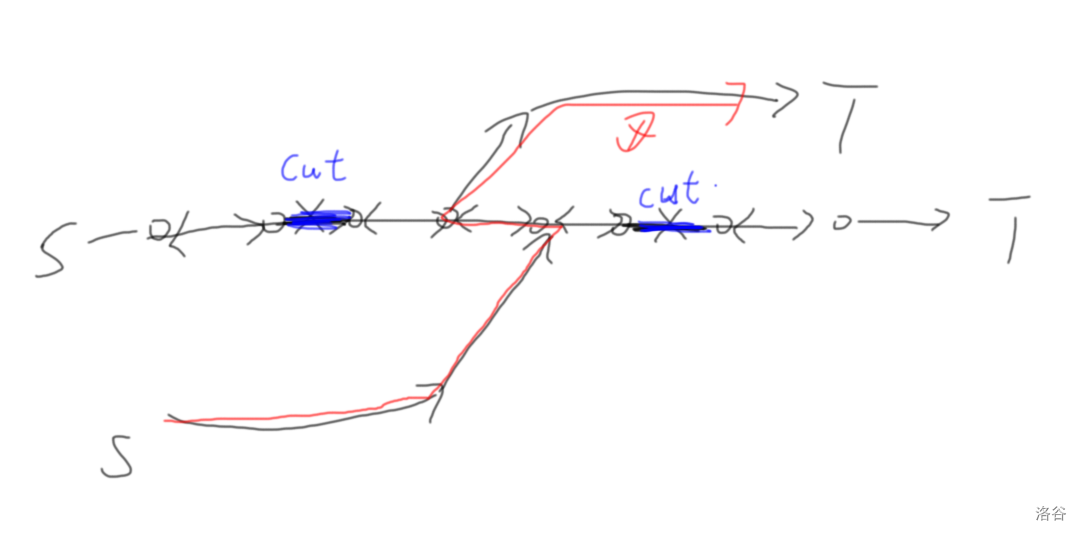
2. 本题的特殊性

但本题相比于 P6054 有个特殊的点：$D\geq 0$

若存在一条链被割两次以上。现基于割掉最小割后的图建一个新图：

对于每条链，若割了若干条边：$((a,k_1),(a,k_1+1)),((a,k_2),(a,k_2+1)),\cdots((a,k_t),(a,k_t+1)),$

那么，建 $t+1$ 个新点 $[a,1],[a,2],\cdots [a,t+1]$，代表被割开的一段一段的链。

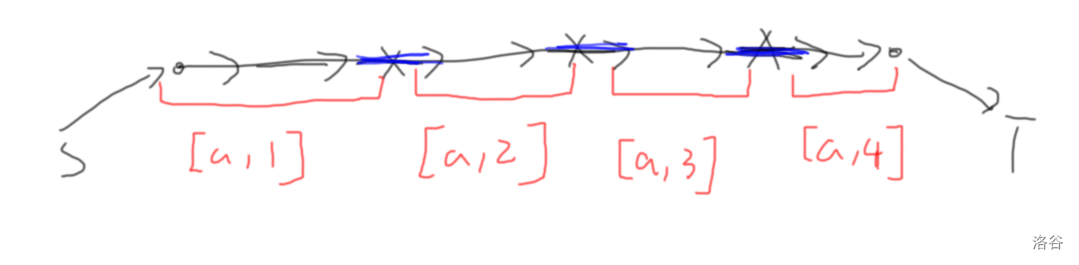
其中，根据前面所说的引理， $[a,2]\cdots,[a,t]$ 里面都存在点可以从 $S$ 到达，也存在点可以到达 $T$。

所以对于 $[a,2]\cdots,[a,t]$ 这些新点，对于每个新点 $[a,k]$，考虑它代表的点的区间所有点 $(a,c)$，若存在边 $((b,c+D),(a,c),\infty)$，且 $S\to (b,c+D)$。 且 $(b,c+D)$ 在 $[b,k']$ 里面，那么从 $[b,k']$ 向 $[a,k]$ 连一条边。

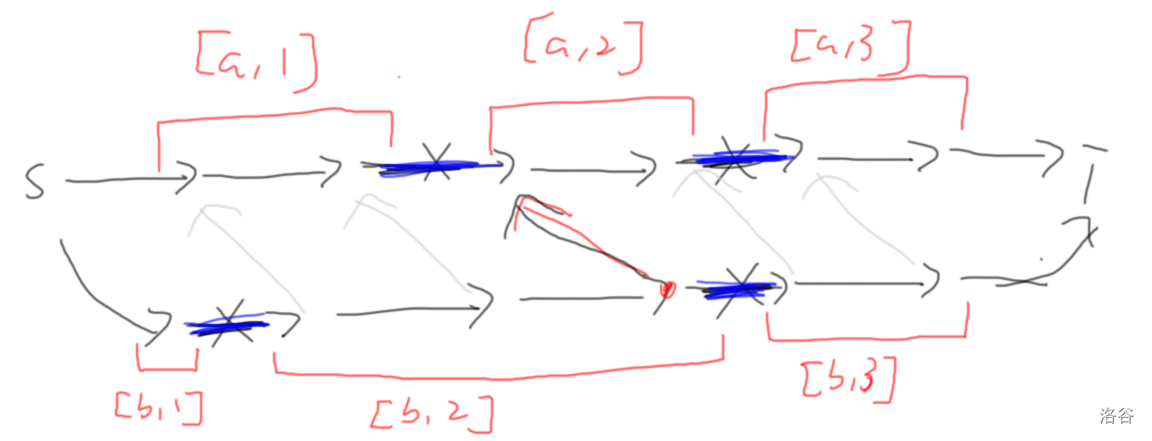（例如本图中，假设 $S\to$ $[b,2]$ 的最后一个点，那么$[b,2]$ 向 $[a,2]$ 连一条边）

由于 $S$ 可以到达 $[a,i]$ （$2\leq i\leq t_a$），那么对于新图，必然存在边 $([a,1],[b,i])$ （$2\leq i\leq t_b$）。因为若不存在这样的边，必然所有点都无法从 $S$ 到达。

那么，考虑 $([a,1],[b,i])$ 这条边存在导致的问题吧。

由于 $D\geq 0$，所以边都是向源点方向连的，所以 $[b,i]$ 里第一个可以被 $[a,1]$ 到达的点必然为最左端点。而可以到达最左端点则意味着可以到达所有点，而回顾之前我们说的一定存在一个点可以到达 $T$，这意味着 $S\to T$，矛盾。

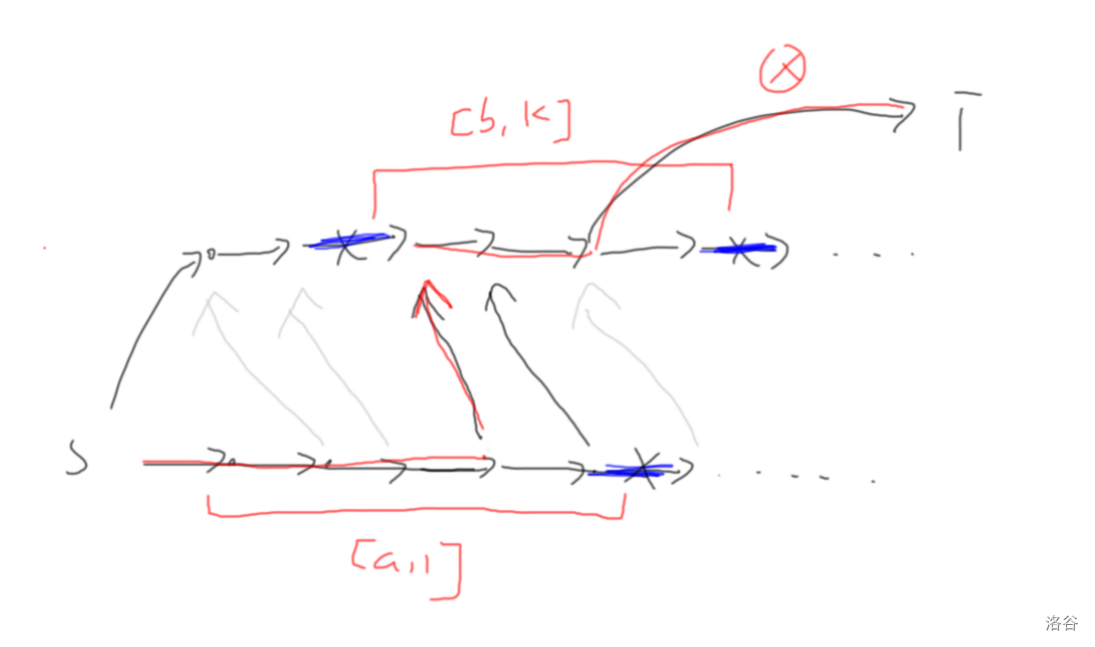
综上，一定不存在点 $[a,i]$ （$2\leq i\leq t_a$），也就是每条链必然割一条边。得证。

至于问我为啥 $D<0$ 这个证明就不行了，考虑：

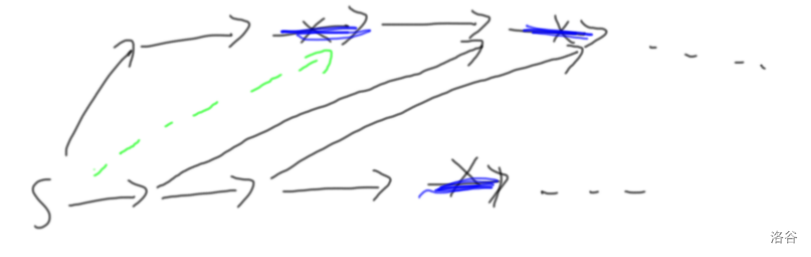
左边的那条虚线边不存在。所以证明无法进行下去。就真的有可能出现两个割边之间，前面一段可以到 $T$ 后面一段可以从 $S$ 到达的合法的两个割边的情况了。

其实根据这个证明不难想到另一种解决 P6054 的方式：手动把缺的那些边补上就好。对于 $a_{v_i}\geq a_{u_i}+k_i$ 的限制，若 $k_i>0$ 那么从 $S$ 开始向 $(v_i,1),\cdots (v_i,k_i)$ 连 $\infty$ 边，把那些缺少的边补上就好。