自动搬运

查看原文

来自洛谷，原作者为

	bzy369258147 **

搬运于2025-08-24 21:46:33，当前版本为作者最后更新于2019-03-14 16:48:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本文旨在探讨关于该题网上流传的唯一一个玄学题解的正确性证明，以及关于该题图的性质的分析.

实名反对楼上的题解关于HNOI2011出题人的评价(大雾

以及这题是一道类似 HNOI2018毒瘤 的 好(毒瘤) 题.

也是一个本质上的 提交答案题.

观察题意不难发现这题是给定图求独立集的个数.

然而对一般图而言这是NP的,所以我们猜想这是一个特殊图.

那它是不是:

链? (X)

树? (X)

基环树? (X)

仙人掌? (?)

二分图? (X)

正则图? (X)

弦图? (X)

那是不是出题人就是毒瘤，就是拿一个NP问题当普通题出出来? (X)

通过观察，我们发现这个图，它，至少，是，一个，平面图...

然而并没有什么X用23333

这是我在求出(1 - 2e5)所有边再拓扑排序以后剩下的图的样子:

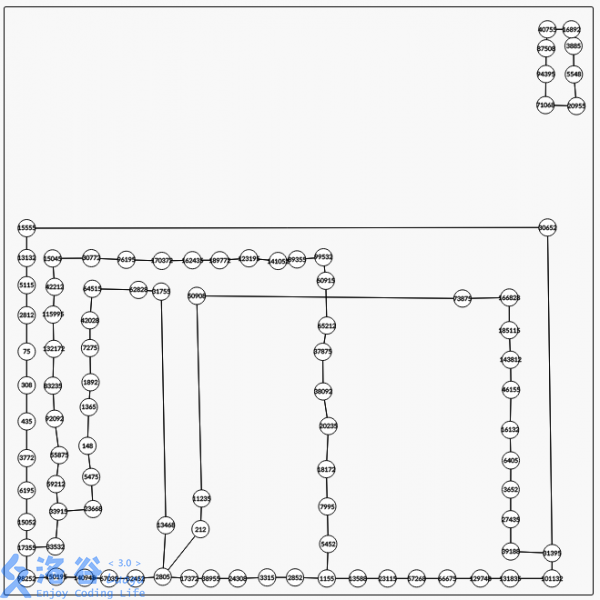
把里边相交的环展到大环外面就是一个平面图了.

这是我在求出(2e4 - 1e6)所有边再拓扑排序以后剩下的图的样子:

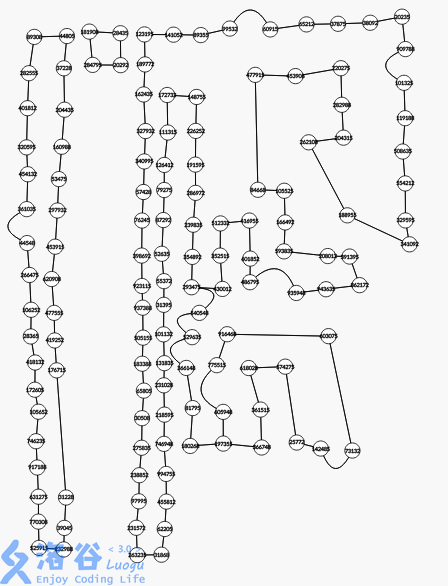
我们发现它甚至是一个沙漠图(仙人掌森林).

也就是说出题人故意安排的部分分其实是有意义的。

具体分3档

30pt(1) : 树形DP

70pt(1 + 3) : 仙人掌DP

100pt(1 + 2 + 3) : 正解.

通过观察发现，原图所有的联通子图中最多比树多3条边，所以这题直接变成了毒瘤的弱化版，所以所谓的玄学做法(毒瘤的部分分做法)自然能过啦.

代码如下:

#include<bits/stdc++.h>
using namespace std;

const int mod = 1e9 + 7;
int PW2[1000005];

const int maxN = 1e6;

int n;
int num[1000005];

vector<int> to[1000005];
bool vis[1000005];
bool ins[1000005];
int  sat[1000005];

vector<int> QE;

void dfs_init( int x, int f ) {
    vis[x] = true;
    for( auto N : to[x] ) if( N ^ f ) {
        if( !vis[N] ) dfs_init( N, x );
        else {
            if( !ins[x] ) QE.push_back( x );
            if( !ins[N] ) QE.push_back( N );
            ins[x] = ins[N] = true;
        }
    }
}

int dp[1000005][2];
int des[1000005];
int pnt = 0;

int dfs_dp( int x ) {
    dp[x][0] = 1; dp[x][1] = PW2[ num[x] ] - 1; des[x] = pnt;
    for( auto N : to[x] ) if( des[N] ^ pnt ) {
        dp[x][0] = 1ll * dp[x][0] * dfs_dp( N ) % mod;
        dp[x][1] = 1ll * dp[x][1] * dp[N][0] % mod;
    }
    if( sat[x] ==  1 ) dp[x][0] = 0;
    if( sat[x] == -1 ) dp[x][1] = 0;
    return ( dp[x][0] + dp[x][1] ) % mod;
}

bool check() {
    for( auto P : QE ) for( auto N : to[P] ) 
      { if( sat[P] == 1 and sat[N] == 1 ) return false; }
    return true;
}

int query(int x) {
    QE.clear(); dfs_init( x, x );
    int ans = 0;
    int len = 1 << QE.size();
    for( int i = 0; i < len; i ++ ) {
        for( int j = 0; j < QE.size(); j ++ ) 
          { sat[ QE[j] ] = (i & (1 << j)) ? 1 : -1; }
        if( check() ) pnt ++, ( ans += dfs_dp( x ) ) %= mod;
    }
    for( int i = 0; i < QE.size(); i ++ ) sat[ QE[i] ] = 0;
    return ans;
}

int main(){
    int n; cin >> n; PW2[0] = 1;
    for(int i = 1;i <= n;i ++) PW2[i] = PW2[i - 1] * 2 % mod;
    for(int i = 1;i <= n;i ++) { int x; cin >> x; num[x] ++; }
    for(int i = 1;i * i <= maxN;i ++) for(int j = i + 1;2 * i * j <= maxN;j ++) {
        if( j * j > 2 * maxN ) break;
        int x = j * j - i * i, y = 2 * i * j;
        if( x > maxN or y > maxN ) continue;
        if( !num[x] or !num[y] or __gcd( x, y ) != 1 ) continue;
        to[x].push_back(y); to[y].push_back(x);
    }
    int ans = 1;
    for(int i = 1;i <= maxN;i ++) if( num[i] and !vis[i] ) 
      { ans = 1ll * ans * query(i) % mod; }
    cout << ( ans - 1 + mod ) % mod;
    return 0;
}

拓扑排序的代码:

#include<bits/stdc++.h>
using namespace std;

int N = 200000;
int M = 0;
int deg[1000005];
vector<int> to[1000005];

int main(){

    for(int i = 2;i <= N;i ++) {
        for(int j = 1;j <= i;j ++) {
            if( 1ll * 2 * i * j > N ) break;
            if( 1ll * i * i - 1ll * j * j > N ) continue;
            if( __gcd( i, j ) > 1 ) continue;
            long long u = i * i - j * j;
            long long v = 2 * i * j;
            if( __gcd( u, v ) > 1 ) continue;
            if( u > v ) swap( u, v );
            if( u < M or v < M ) continue;
            deg[u] ++; deg[v] ++; to[u].push_back(v); to[v].push_back(u);
            //printf( "%d %d\n", u, v );
        }
    }
    queue<int> Q;
    for(int i = 1;i <= N;i ++) if( deg[i] == 1 ) Q.push(i);
    while( !Q.empty() ) {
        int x = Q.front(); Q.pop();
        for( auto N : to[x] ) {
            deg[N] --;
            if( deg[N] == 1 ) Q.push( N );
        }
    }
    for(int i = 1;i <= N;i ++) if( deg[i] > 1 )for( auto E : to[i] ) if( deg[E] > 1 ) printf( "%d %d\n", i, E );
    //for(int i = 1;i <= N;i ++) if( deg[i] > 1 ) printf( "%d %d\n", i, deg[i] );
    return 0;
}