自动搬运

查看原文

来自洛谷，原作者为

	p_b_p_b *const int brain=NULL;

搬运于2025-08-24 21:46:20，当前版本为作者最后更新于2019-01-24 20:15:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本题最好的一篇题解的图片似乎咕咕咕了，那我来补一篇吧，顺便发个计算几何板子。

首先你画画图，发现一个性质：从上往下看能看到的图像一定是一个下凸的图像，像这样：

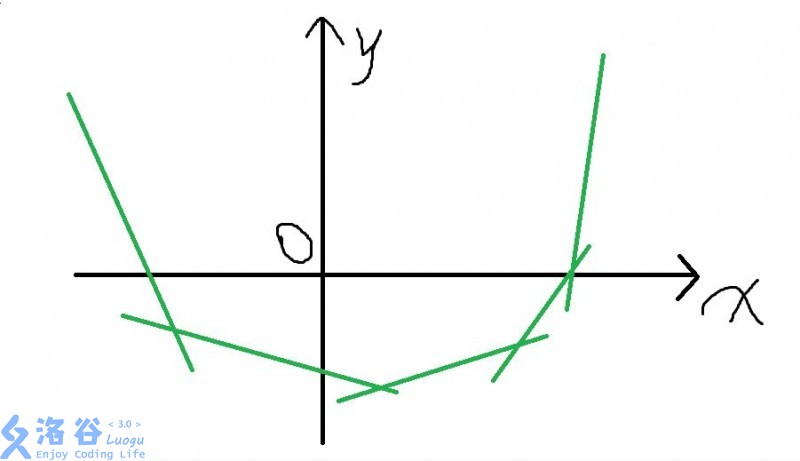
至于为什么嘛……画下图就出来了。

再观察一下：从左往右，斜率递增。

那么做法就很明显了：

· 直线以斜率为第一关键字，截距为第二关键字排序；

· 维护一个单调栈记录当前能看见的直线编号；

· 每次加入一条直线就把栈顶被覆盖的直线丢掉（用直线交点判一下就好了）。

· 输出答案。

我的代码巨长无比，因为有其他计算几何的模板。推荐一个挺好的学习笔记：https://www.cnblogs.com/candy99/p/6360536.html 。Candy?太神仙了。（然而那里面的线段相交似乎挂了）

代码：

#include<bits/stdc++.h>
namespace my_std{
	using namespace std;
	#define pii pair<int,int>
	#define fir first
	#define sec second
	#define MP make_pair
	#define rep(i,x,y) for (int i=(x);i<=(y);i++)
	#define drep(i,x,y) for (int i=(x);i>=(y);i--)
	#define go(x) for (int i=head[x];i;i=edge[i].nxt)
	#define sz 50505
	typedef long long ll;
	template<typename T>
	inline void read(T& t)
	{
		t=0;char f=0,ch=getchar();
		double d=0.1;
		while(ch>'9'||ch<'0') f|=(ch=='-'),ch=getchar();
		while(ch<='9'&&ch>='0') t=t*10+ch-48,ch=getchar();
		if(ch=='.')
		{
			ch=getchar();
			while(ch<='9'&&ch>='0') t+=d*(ch^48),d*=0.1,ch=getchar();
		}
		t=(f?-t:t);
	}
	template<typename T,typename... Args>
	inline void read(T& t,Args&... args){read(t); read(args...);}
	void file()
	{
		#ifndef ONLINE_JUDGE
		freopen("a.txt","r",stdin);
		#endif
	}
//	inline ll mul(ll a,ll b){ll d=(ll)(a*(double)b/mod+0.5);ll ret=a*b-d*mod;if (ret<0) ret+=mod;return ret;}
}
using namespace my_std;

#define I inline
typedef double db;
const db eps=1e-8;
I int dcmp(db x){return fabs(x)<=eps?0:(x>0?1:-1);}
struct Vector
{
	db x,y;
	Vector(db xx=0,db yy=0){x=xx,y=yy;}
	I const Vector operator + (const Vector &a) const {return Vector(x+a.x,y+a.y);}
	I const Vector operator - (const Vector &a) const {return Vector(x-a.x,y-a.y);}
	I const Vector operator * (const db &a) const {return Vector(x*a,y*a);}
	I const Vector operator / (const db &a) const {return Vector(x/a,y/a);}
	I const bool operator < (const Vector &a) const {return dcmp(x-a.x)==0?dcmp(y-a.y)<0:dcmp(x-a.x)<0;}
	I const bool operator == (const Vector &a) const {return dcmp(x-a.x)==0&&dcmp(y-a.y)==0;}
	I const bool operator != (const Vector &a) const {return dcmp(x-a.x)!=0||dcmp(y-a.y)!=0;}
};
typedef Vector Point;
I Vector Normal(Vector a){return Vector(-a.y,a.x);} // counterclockwise
I db Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
I db Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
I db Len(Vector a){return sqrt(Dot(a,a));}
I db Len2(Vector a){return Dot(a,a);}
I db Angle(Vector a,Vector b){return acos(Dot(a,b)/Len(a)/Len(b));}
I Vector Rotate(Vector a,db rad){return Vector(cos(rad)*a.x-sin(rad)*a.y,sin(rad)*a.x+cos(rad)*a.y);}
struct Line
{
	Point a,b; // a->b
	Line(){}
	Line(Point aa,Point bb){a=aa,b=bb;}
};
I db DisL(Point p,Line l){Vector u=p-l.a,v=l.b-l.a;return fabs(Cross(u,v))/Len(v);} // dist to line
I db DisS(Point p,Point a,Point b) // dist to segment
{
	if (a==b) return Len(p-a);
	Vector v1=b-a,v2=p-a,v3=p-b;
	if (dcmp(Dot(v1,v2))<0) return Len(v2);
	if (dcmp(Dot(v1,v3))>0) return Len(v3);
	return fabs(Cross(v1,v2))/Len(v1);
}
I bool OnLeft(Point p,Line l){return dcmp(Cross(p-l.a,l.b-l.a))<=0;}
I bool OnLine(Point p,Line l){return dcmp(Cross(p-l.a,l.a-l.b))==0;}
I bool OnSeg(Point p,Point a,Point b){return dcmp(Cross(p-a,a-b))==0&&dcmp(Cross(p-a,p-b))<0&&p!=a&&p!=b;}
I Point LI(Line l1,Line l2) // line intersection
{
	Vector v=l1.a-l2.a,v1=l1.b-l1.a,v2=l2.b-l2.a;
	db t=Cross(v,v2)/Cross(v2,v1);
	return l1.a+v1*t;
}
I bool LSI(Line l,Point a,Point b) // line-seg intersection
{
	Vector v=l.b-l.a,v1=a-l.a,v2=b-l.a;
	return dcmp(Cross(v,v1))!=dcmp(Cross(v,v2));
}
I bool SSI(Point a1,Point b1,Point a2,Point b2) /*seg-seg intersection*/ {Line l1(a1,b1),l2(a2,b2);return LSI(l1,a2,b2)&&LSI(l2,a1,b1);}
I Point Circumcenter(Point a,Point b,Point c) // wai xin
{
	Point p=(a+b)/2,q=(a+c)/2;
	Vector u=Normal(b-a),v=Normal(c-a);
	if (!dcmp(Len(a-b)+Len(a-c)-Len(b-c))) return (b+c)/2;
	if (!dcmp(Len(a-b)+Len(b-c)-Len(a-c))) return (a+c)/2;
	if (!dcmp(Len(a-c)+Len(b-c)-Len(a-b))) return (a+b)/2;
	return LI(Line(p,p+u),Line(q,q+v));
}
I Point Barycenter(Point a,Point b,Point c) /*zhong xin*/ {return (a+b+c)/3;}
I bool PolarCmp(Point a,Point b){db c=Cross(a,b);return dcmp(c)==0?a.x<b.x:dcmp(c)>0;}
db PolygonArea(Point *p,int n)
{
	db ret=0;
	rep(i,2,n-1) ret+=Cross(p[i]-p[1],p[i+1]-p[1]);
	return fabs(ret/2);
}
int InPolygon(Point *poly,int n,Point p) // 1:in 0:out -1:on
{
	int ret=0;
	rep(i,1,n)
	{
		int j=i%n+1;
		if (OnSeg(p,poly[i],poly[j])||p==poly[i]||p==poly[j]) return -1;
		if (poly[i].y==poly[j].y) continue;
		int tmp=(poly[i].y>poly[j].y?i:j);
		if (p.y==poly[tmp].y&&p.x<poly[tmp].x) { ret^=1; continue; }
		tmp=(poly[i].y<poly[j].y?i:j);
		if (p.y==poly[tmp].y&&p.x<poly[tmp].x) continue;
		if (SSI(p,p+Vector(1e18,0),poly[i],poly[j])) ret^=1;
	}
	return ret;
}
bool IsConvex(Point *poly,int n)
{
	int now=0,last=0;
	rep(i,1,n)
	{
		int j=i+1,k=i+2;j>n?j-=n:0;k>n?k-=n:0;
		now=dcmp(Cross(poly[k]-poly[j],poly[j]-poly[i]));
		if (now*last<0) return 0;
		last=now;
	}
	return 1;
}
int GetConvex(Point *p,int n,Point *ret) // return the size of the convex
{
	sort(p+1,p+n+1);n=unique(p+1,p+n+1)-p-1;
	int m=0;
	rep(i,1,n)
	{
		while (m>1&&dcmp(Cross(ret[m]-ret[m-1],p[i]-ret[m-1]))<=0) --m;
		ret[++m]=p[i];
	}
	int _m=m;
	drep(i,n-1,1)
	{
		while (m>_m&&dcmp(Cross(ret[m]-ret[m-1],p[i]-ret[m-1]))<=0) --m;
		ret[++m]=p[i];
	}
	if (n>1) --m;
	return m;
}
db RotatingCalipers(Point *p,int n)
{
	db ret=0;
	if (n==1) return ret;
	if (n==2) return Len(p[1]-p[2]);
	int now=1;Point _=p[n+1];p[n+1]=p[1];
	rep(i,1,n)
	{
		while (dcmp(DisL(p[now],Line(p[i],p[i+1]))-DisL(p[now+1],Line(p[i],p[i+1])))<0) now=now%n+1;
		ret=max(ret,max(Len(p[now]-p[i]),Len(p[now]-p[i+1])));
	}
	p[n+1]=_;
	return ret;
}
db MinCircleCover(Point *p,int n,Point &O) // return the minimum radius
{
	O=p[1];db r=0;
	rep(i,2,n) if (dcmp(r-Len(p[i]-O))<0)
	{
		O=p[i],r=0;
		rep(j,1,i-1) if (dcmp(r-Len(p[j]-O))<0)
		{
			O=(p[i]+p[j])/2,r=Len(O-p[j]);
			rep(k,1,j-1) if (dcmp(r-Len(p[k]-O))<0)
			{
				O=Circumcenter(p[i],p[j],p[k]);
				r=Len(O-p[k]);
			}
		}
	}
	return r;
}

int n;
struct hh{db k,b;int id;}a[sz];
inline bool cmp(const hh &x,const hh &y){return x.k==y.k?x.b>y.b:x.k<y.k;}
Line aa[sz];
int top,s[sz];

int main()
{
	file();
	db x,y;
	read(n);
	rep(i,1,n) read(x,y),a[i]=(hh){x,y,i};
	sort(a+1,a+n+1,cmp);
	rep(i,1,n) aa[i].a=Point(0,a[i].b),aa[i].b=Point(1,a[i].k+a[i].b);
	s[top=1]=1;
	rep(i,2,n) if (a[i].k!=a[i-1].k)
	{
		while (top>1&&dcmp(LI(aa[s[top]],aa[s[top-1]]).x-LI(aa[s[top-1]],aa[i]).x)>=0) --top;
		s[++top]=i;
	}
	rep(i,1,top) s[i]=a[s[i]].id;
	sort(s+1,s+top+1);
	rep(i,1,top) printf("%d ",s[i]);
}