自动搬运

查看原文

来自洛谷，原作者为

	George1123 **

搬运于2025-08-24 21:45:55，当前版本为作者最后更新于2020-01-04 12:08:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

${\color{#cc0055}\text{欢迎拜访我这个蒟蒻的博客}}$

P3159 【[CQOI2012]交换棋子】

此题算法:费用流

题目很简洁，做法很恶心的典型。

因为是网络流题，所以模板就不说了，只考虑加边。

大致思路：

简化问题

记录初始和结束状态，把白棋看作没棋。

把开始结束都有黑棋的格子看作没棋。

如果开始结束时黑棋数不等，$-1$ 掉。

加边

1.拆点，每个格子有格子 $x$和格子 $y$。

控制格子交换次数。

2.$s$ 向每个黑棋格 $x$ 连流量 $1$ 费用 $0$ 的边。

表示需匹配状态。

3.每个黑棋格 $y$ 向 $t$ 连流量 $1$ 费用 $0$ 的边。

表示匹配状态。

4.每个格子 $x$ 向对应 $y$ 连流量 $($允许交换数$\div 2)$ 费用 $0$的边。

两次交换只会消耗 $1$ 的流量。

※.如果格子初始或结束时有黑棋并且允许交换数为奇数，在上面那条边上附上 $1$的流量。

不交换本来就要通过的流量。

5.每个格子 $y$ 向八连通的格子 $x$ 连流量 $\inf$ 费用 $1$ 的边。

用来交换。

然后跑模板就好了，网络流的题都差不多。

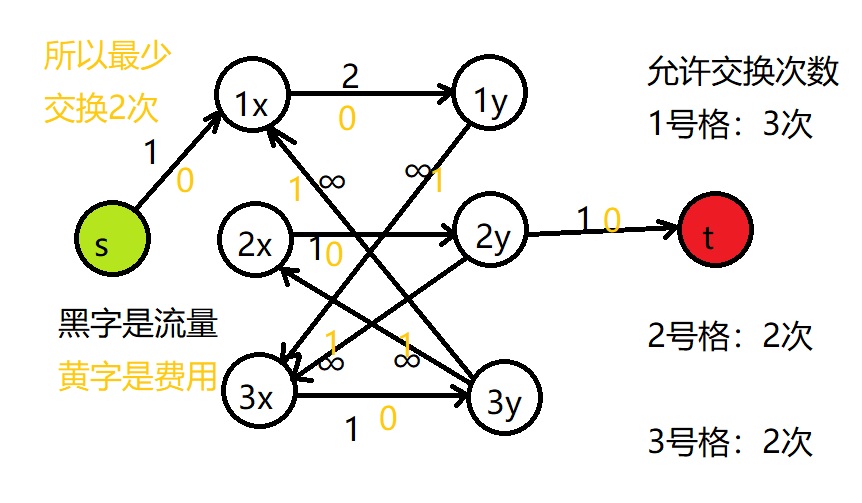
图片仅供参考，以实物为准。

以下是代码 $+$ 注释

#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
const int M=5e4+10;
const int inf=1e8+10;
int p,n,m,s,t,S,T,fans,cans;
struct edge{
	int adj,nex,fw,r;
}e[M];
int g[N],top=1;
void add(int x,int y,int z,int w){
	e[++top]=(edge){y,g[x],z,w};
	g[x]=top;
}
void Add(int x,int y,int z,int w){
	add(x,y,z,w),add(y,x,0,-w);
}
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool spfa(){
	// puts("spfa()");
	for(int i=1;i<=p;i++)
		vis[i]=0,dep[i]=inf,cur[i]=g[i];
	Q.push(s),vis[s]=1,dep[s]=0;
	while(Q.size()){
		int x=Q.front(); Q.pop();
		vis[x]=0;
		for(int i=g[x];i;i=e[i].nex){
			int to=e[i].adj,d=e[i].r;
			if(e[i].fw&&dep[to]>dep[x]+d){
				dep[to]=dep[x]+d;
				if(!vis[to]){
					vis[to]=1;
					Q.push(to);
				}
			}
		}
	}
	return dep[t]!=inf;
}
int dfs(int x,int F){
	// puts("dfs");
	if(!F||x==t)
		return F;
	int flow=0,f;
	vis[x]=1;
	for(int i=cur[x];i;i=e[i].nex){
		int to=e[i].adj; cur[x]=i;
		if(!vis[to]&&dep[x]+e[i].r==dep[to]&&
		(f=dfs(to,min(F,e[i].fw)))>0){
			e[i].fw-=f;
			e[i^1].fw+=f;
			flow+=f,F-=f;
			if(!F){
				vis[x]=0;
				break;
			} 
		}
	}
	return flow;
}
int P(int x,int y){return (x-1)*m+y;} //点序
int tx[]={-1,1,0,0,-1,-1,1,1};
int ty[]={0,0,-1,1,1,-1,1,-1}; //八向
int Ss[25][25],Ts[25][25]; //初始，终局
int main(){
	scanf("%d%d",&n,&m);
	p=t=2*n*m+2,s=t-1;
	char c[25];
	for(int i=1;i<=n;i++){
		scanf("%s",c);
		for(int j=1;j<=m;j++)
			if(c[j-1]=='1')
				Ss[i][j]=1,S++;
				
	}
	for(int i=1;i<=n;i++){
		scanf("%s",c);
		for(int j=1;j<=m;j++)
			if(c[j-1]=='1')
				Ts[i][j]=1,T++;
	}
	if(S!=T) return puts("-1"),0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(Ss[i][j]&&!Ts[i][j])
				Add(s,P(i,j),1,0),fans++; //2
			if(!Ss[i][j]&&Ts[i][j])
				Add(P(i,j)+n*m,t,1,0);   //3
		}
	}
	for(int i=1,x;i<=n;i++){
		scanf("%s",c);
		for(int j=1;j<=m;j++){
			x=c[j-1]-'0';
			Add(P(i,j),P(i,j)+n*m,x>>1,0); //4
			if((Ss[i][j]^Ts[i][j])&&(x&1))
				Add(P(i,j),P(i,j)+n*m,1,0); //※
			for(int k=0;k<8;k++){
				int xt=i+tx[k],yt=j+ty[k];
				if(xt<1||xt>n||yt<1||yt>m)
					continue;
				Add(P(i,j)+n*m,P(xt,yt),inf,1); //5
			}
		}
	}
	while(spfa()){
		int d=dfs(s,inf);
		fans-=d;
		cans+=d*dep[t];
	}
	if(fans) puts("-1");
	else printf("%d\n",cans);
	return 0;
}

图是手画的，写题解不易。

关注博主，为文章点赞是你应该做的。

谢谢大家! !