自动搬运

查看原文

来自洛谷，原作者为

	zundamon WOOOOOOOOO

搬运于2025-08-24 21:44:43，当前版本为作者最后更新于2023-07-05 11:32:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先可以想到，先对于所有的连通块进行计算贡献

运用乘法原理，将每个连通块的贡献相乘

定义一个连通块的贡献为它的可行方案数，下面开始分类讨论

对于存在环的连通块

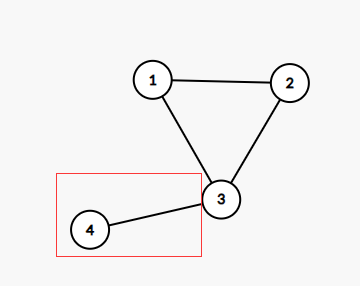
这边发现，右边的环中，每个点都必须收入一条边，有两种可行方案

所以 $4$ 号点所连接的唯一一条边，必须与 $4$ 号点分为一组，有一种可行方案

易得：对于一个连通块，若块中存在环，则贡献为 $2$

对于不存在环的连通块

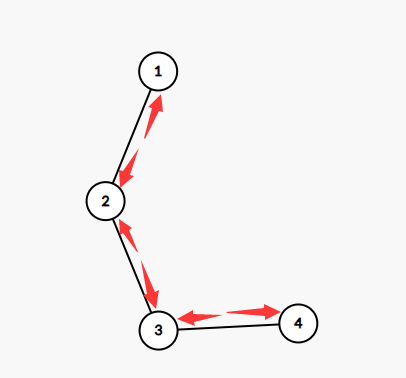
可以发现，这类连通块有 $n$ 个点，$n-1$ 条边

一定存在一个点是没有被分到边的

在 $n$ 个点中选取 $1$ 个没有被分到边的点，贡献为 $C_n^1 = n$

对于边数大于点数的连通块

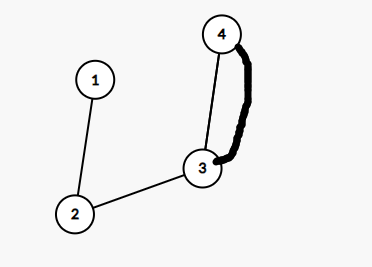
一定存在一个边没有被分配到点，不符合要求，方案为 $0$。

所以遇到这种连通块时，直接全局判 $0$ 即可。

现在问题转化为了：对于每个连通块，判断是否存在环，及点数与边数的关系

对于判环，也可以转化为点数与边数的关系：

随便作一个环，就可以发现，环中的点数 = 边数

而边数可通过 $\text{所有点的出度入度之和} / 2$ 得出

整理得到：

对于每一个连通块：
   点数 > 边数： 为无环，贡献为点数
   点数 = 边数： 为有环，贡献为 2
   点数 < 边数： 不可行，答案为 0
   
最后将每个连通块的贡献相乘即可

代码：

#define loop(i,x,y) for(int i=x;i<=y;i++)
#define doop(i,x,y) for(int i=x;i>=y;i--)
using namespace std;
const int Mod=1000000007;
const long long N=1e6+5;
ll n,m,xx,yy;
ll to[N],hd[N],nxt[N],tot;
void add(ll u,ll v){
	nxt[++tot]=hd[u];
	to[tot]=v;
	hd[u]=tot;
}
ll edg,pts;
void dfs(ll p){
	vis[p]=1,pts++;
	for(int i=hd[p];~i;i=nxt[i],edg++){
		if(!vis[to[i]]) dfs(to[i]);
	}
}
signed main(){
	memset(hd,-1, sizeof hd);
	n=read(),m=read();
	loop(i,1,m){
		xx=read(),yy=read();
		add(xx,yy),add(yy,xx);
	}
	ll ans=1;
	loop(i,1,n){
		
		if(!vis[i]){
			pts=edg=0;
			dfs(i);
			if(pts>edg/2) ans=(ans*pts)%Mod;
			else if(pts==edg/2) ans=(ans*2)%Mod;
			else {ans=0;break;}
		} 
	}
	cout<<ans;
	return 0;
}