自动搬运

查看原文

来自洛谷，原作者为

	泥土笨笨 《算法竞赛实战笔记》作者

搬运于2025-08-24 21:44:40，当前版本为作者最后更新于2020-03-06 15:33:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Farmer John有n个农场，编号为1到n，每个农场在二维平面上，有一个坐标。现在他想按照编号的顺序一次访问每个农场，从1号到2号，再到3号……最后从n号回到1号。每次只能从当前位置走到当前位置的上下左右四个点，每走一步需要花1分钟，每个顶点只能访问一次，问走完一圈回到1点的最短时间是多少。

既然访问顺序是确定的，那么我们可以用单源最短路径算法，比如Dijkstra算法，分别计算从1到2的最短路径，2到3的最短路径……然后全部相加就是答案了。那么问题就转化成了如何求两点间的最短路径，比如我们先考虑按照题目中的样例，从2号到3号点的最短路径是多少。

把样例画成图看一下：

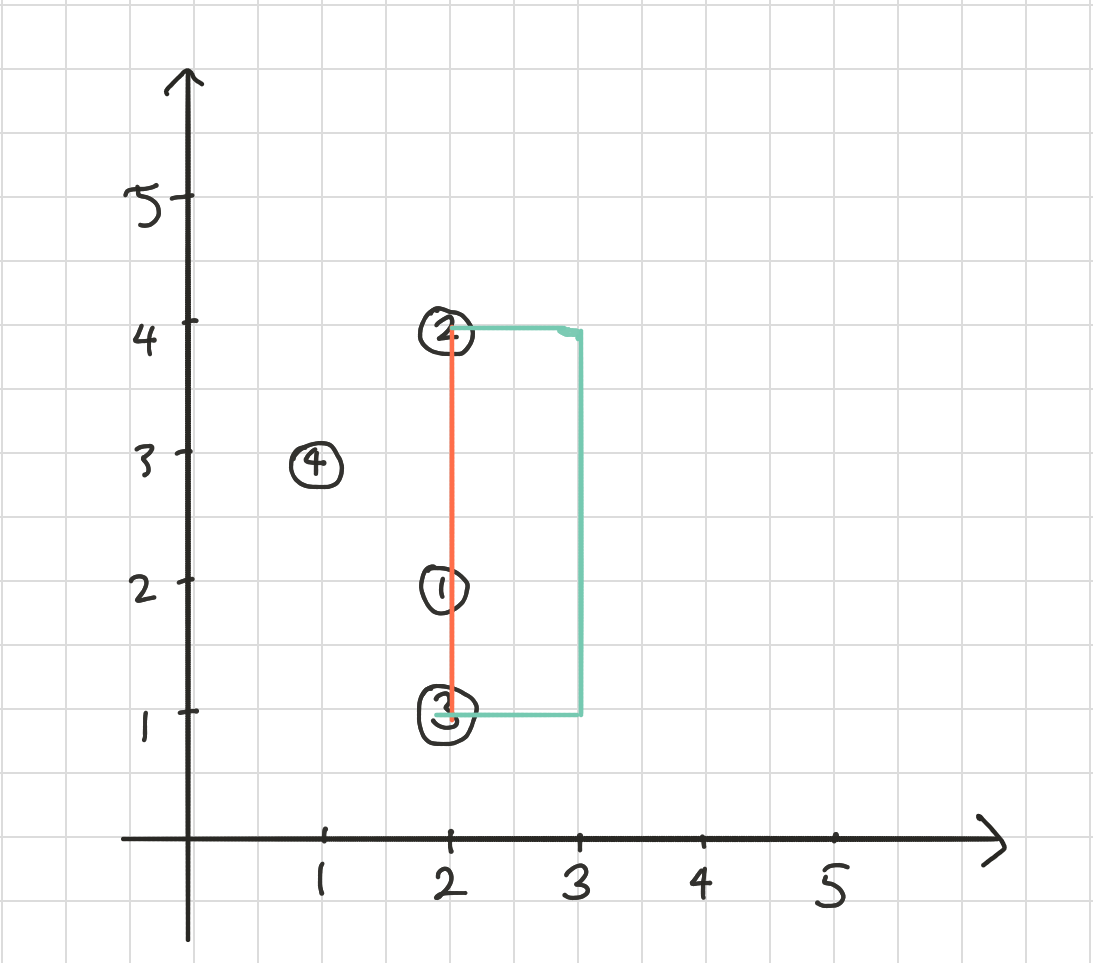
2号点到3号点，直接连下来是最快的，只要3分钟，就是红色的线。但是现在我们要从2号点直接走到3号点，中间不能经过无关的农场1，所以只能走绿色的线，所以从2到3的最短路径是5。

那么如何实现这种不经过农场的最短路径呢？这里有一个小技巧，加虚点。我们在每个点的上下左右，再加4个点。如下图，把虚点都加上：

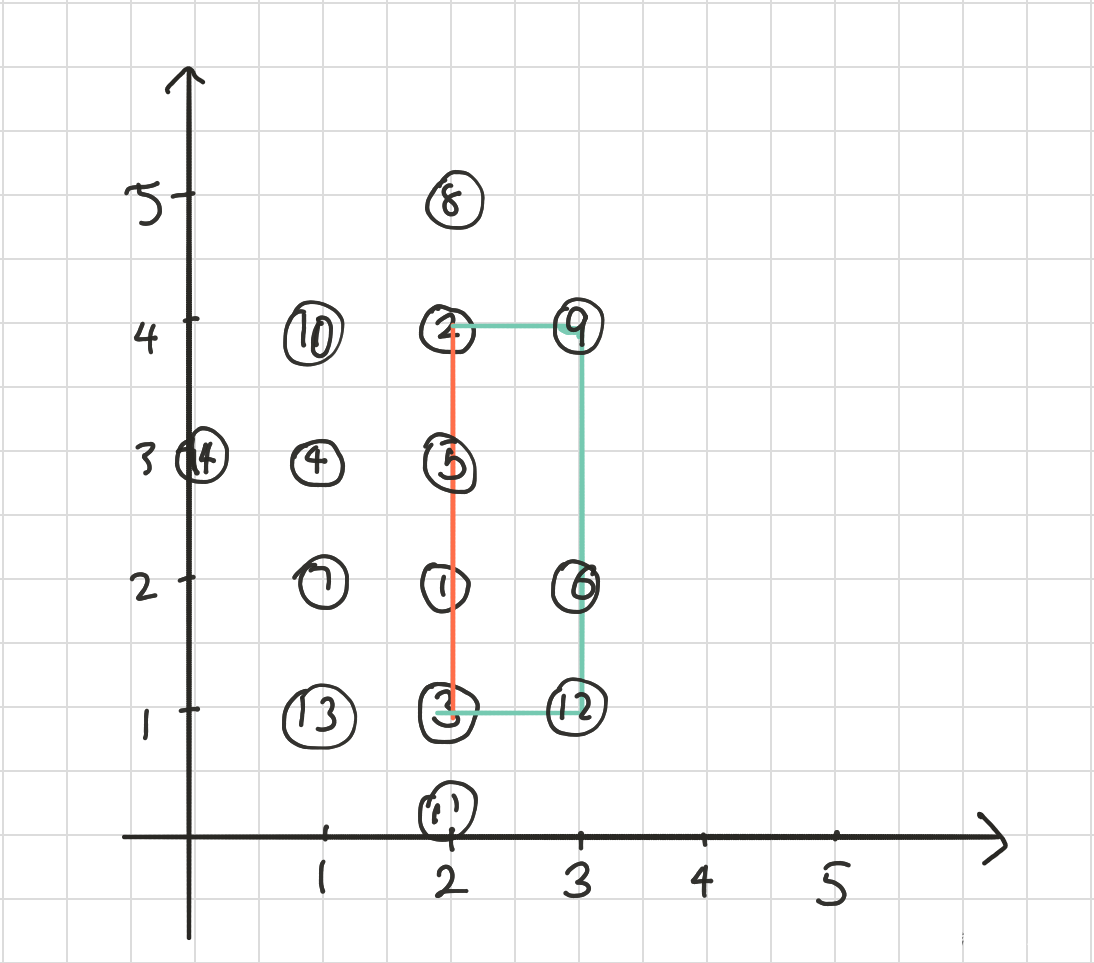
好，那么我们现在有14个点。把每个农场和周围的四个点之间连一条长度为1的边，然后在虚点之间两两连边。比如2到9连一条边，9到6连一条边，6到12连一条边，12到3连一条边。我们要求走最短路径的时候，只能沿着我们连的边走，不能随便乱走。并且走的时候不能碰到别的农场。这样红色的路径2-5-1-3因为碰到了1号而不能走，而2-9-6-12-3这条路径是可以的。

我们这样连边以后跑最短路，一定是比较优秀的，因为如果路线经过了不存在的点，就会”绕远“。比如9号点和12号点的右边没有点了。如果你从9号点向右走，然后下来，然后到12号点的右边，再走回到12号点，你会发现这样绕路了，这样的路是不划算的。

那么是否任意两个虚点之间都连边呢？也不是。我们定义一个概念，”最多拐弯一次的路径“，就是两点之间的路径，要么是直线，要么最多只能有一个直角拐弯，不能有两个或者两个以上。比如图中2号点左边的10号点，和3号点下面的11号点，这两个点之间，就找不到一条路径可以最多拐一个直角弯就能相连。这样10号点和11号点我们就不连边，因为如果要拐超过一个弯，这个路线一定要绕路。事实上，10号到11号点，可以走10-14-7-12-11这条路径，这条路径是不绕路的，所以并不需要在他们之间多连一条绕路的边。

那么只要虚点之间的边都不绕路，那么虚点之间的路径的长度就是他们之间的曼哈顿距离，即两点之间横坐标的差的绝对值，加上纵坐标的差的绝对值。

下一个难点是如何判断两个点之间可以有一条”最多拐弯一次的路径“，而且要求这个路径不能经过农场呢？如果这两个点本来就在同一行或者同一列，问题就退化成了判断农场点在不在线段上，这个好解决。如果两个点不在同一行同一列，那么因为他们最多拐一次弯，所以只有两条路线可以走，如下图：

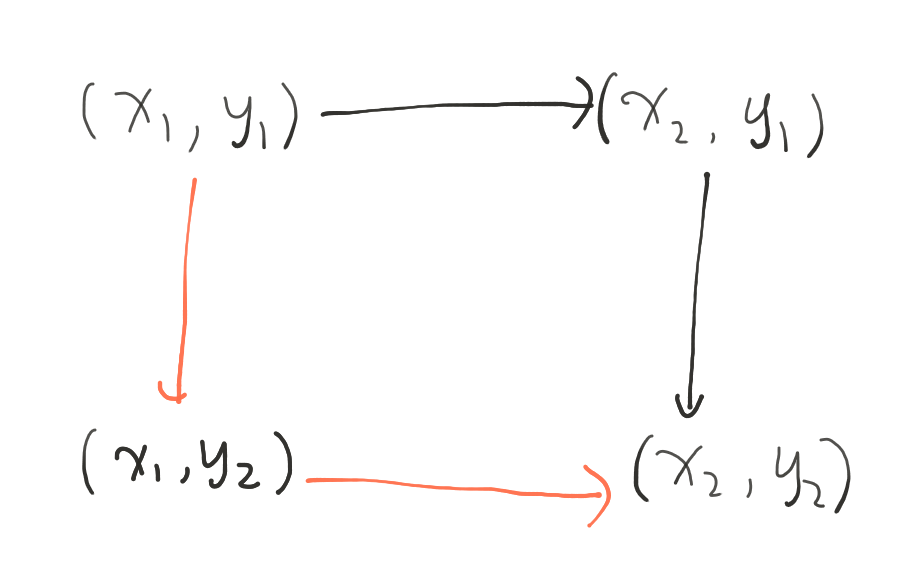
从(x1,y1)点走到(x2，y2)点，要么走黑色路径，要么走红色路径。每条路径可以拆成两个线段，于是又退化为点在线段上的判断。

基本思路讲完了，其他就是代码了：

#include <iostream>
#include <map>
#include <vector>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;
const int MAXN = 505;

struct Point {
    int x, y;

    Point(int x, int y) : x(x), y(y) {}

    bool operator<(const Point &a) const {
        if (x != a.x) return x < a.x;
        return y < a.y;
    }
};

struct Edge {
    int v, w;

    Edge(int v, int w) : v(v), w(w) {}
};

struct Node {
    int u, d;

    Node(int u, int d) : u(u), d(d) {}

    bool operator<(const Node &a) const {
        return d > a.d;
    }
};

int n, x[MAXN], y[MAXN], nn, ans, dis[MAXN], vis[MAXN];//nn表示点的总个数
map<Point, int> dict;//定义一个集合，用来判断某个点是否重复出现过
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
vector<Edge> adj[MAXN];

//判断p点在不在线段(x1,y1),(x2,y2)上
bool inSegment(int p, int x1, int y1, int x2, int y2) {
    if (x1 == x2 && x[p] == x1) {
        if (y1 > y2) swap(y1, y2);
        if (y[p] >= y1 && y[p] <= y2) return true;
    }
    if (y1 == y2 && y[p] == y1) {
        if (x1 > x2) swap(x1, x2);
        if (x1 <= x[p] && x[p] <= x2) return true;
    }
    return false;
}

//判断一条线段是否穿过任何一个农场
bool valid(int x1, int y1, int x2, int y2) {
    for (int i = 1; i <= n; ++i) {
        if (inSegment(i, x1, y1, x2, y2)) return false;
    }
    return true;
}

//判断p1和p2点能否连通，连通的条件是有至少一条最多一个直角的路径，不经过其他农场
bool connect(int p1, int p2) {
    if (x[p1] == x[p2] || y[p1] == y[p2]) {
        return valid(x[p1], y[p1], x[p2], y[p2]);
    }
    if (valid(x[p1], y[p1], x[p2], y[p1]) && valid(x[p2], y[p1], x[p2], y[p2])) return true;
    return valid(x[p1], y[p1], x[p1], y[p2]) && valid(x[p1], y[p2], x[p2], y[p2]);
}

int manhattan(int p, int q) {
    return abs(x[p] - x[q]) + abs(y[p] - y[q]);
}

void dijkstra(int start, int target) {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    dis[start] = 0;
    priority_queue<Node> q;
    q.push(Node(start, 0));
    while (!q.empty()) {
        int u = q.top().u;
        q.pop();
        if (vis[u]) continue;
        vis[u] = 1;
        for (int i = 0; i < adj[u].size(); ++i) {
            int v = adj[u][i].v;
            if (v <= n && v != target) continue;
            int w = adj[u][i].w;
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                q.push(Node(v, dis[v]));
            }
        }
    }
}

int main() {
    //先输入每个点的数据
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> x[i] >> y[i];
        dict[Point(x[i], y[i])] = i;
    }
    nn = n;
    //把每个点上下左右四个点也加进来，重复的就不要了
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j < 4; ++j) {
            int xx = x[i] + dx[j];
            int yy = y[i] + dy[j];
            Point p = Point(xx, yy);
            if (dict.count(p) == 0) {
                ++nn;
                x[nn] = xx;
                y[nn] = yy;
                dict[p] = nn;
            }
            int id = dict[p];
            adj[i].push_back(Edge(id, 1));
            adj[id].push_back(Edge(i, 1));
        }
    }
    //建边
    for (int i = n + 1; i <= nn; ++i) {
        for (int j = i + 1; j <= nn; ++j) {
            if (connect(i, j)) {
                int d = manhattan(i, j);
                adj[i].push_back(Edge(j, d));
                adj[j].push_back(Edge(i, d));
            }
        }
    }
    for (int i = 1; i <= n; ++i) {
        int target = i + 1;
        if (i == n) target = 1;
        dijkstra(i, target);
        if (dis[target] == 0x3f3f3f3f) {
            cout << -1 << endl;
            return 0;
        }
        ans += dis[target];
    }
    cout << ans << endl;
    return 0;
}