自动搬运

查看原文

来自洛谷，原作者为

	Water_Cows 这个人不懒，终于找到了 ta

搬运于2025-08-24 21:44:30，当前版本为作者最后更新于2021-02-12 14:43:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

吐槽一句，题解里面写的都是啥啊。。。威佐夫博弈对于我们这些蒟蒻来说，太难了。

---

$\texttt{UPDATE 2021.2.13}$ 代码添加注释，修改一些 $\LaTeX$。 $\texttt{UPDATE 2021.3.6}$ 修改一些细节。

Part 1 找规律

在模拟赛上看到这种题，第一眼看到的就应该想到找规律。

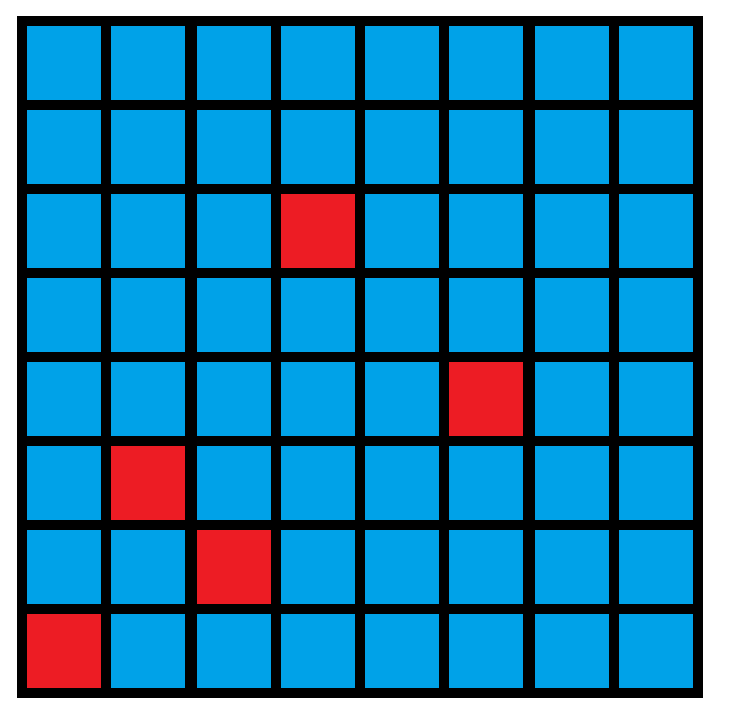
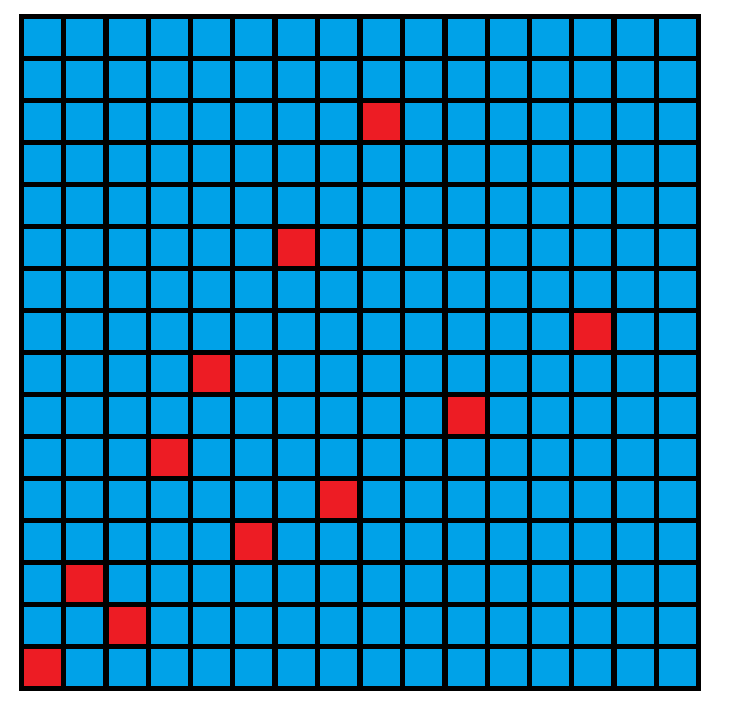
我们首先把胜负的图画出来。注：红色表示 Farmer John 胜，蓝色表示 Bessie 胜。

感觉太少了，没关系，再来！

感觉我的手要断了。

有兴趣的读者可以继续画下去，反正我是不画了。

我们把每个点的坐标写出来：

$$(0, 0), (1, 2), (2, 1), (3, 5), (4, 7), (5, 3), (6, 10), (7, 4), (8, 13), (10, 6), (13, 8) $$

我们发现，哦不，没有发现，这毛玩样有什么（毛个）规律啊？

但是有一点我们可以发现，就是红色的东西是关于 $y=x$ 这条直线对称的（说给初一及以下的同学听，就是关于正方形对角线对称的）。

好，那我们重新写一遍出来：

$$(0, 0), (1, 2), (3, 5), (4, 7), (6, 10), (8, 13)$$

还是没什么规律啊？把一个点横纵坐标做个差看看？

$$0, 1, 2, 3, 4, 5$$

！！！发现了吧，等差数列！！！

Part 2 得出规律

所以可以得出规律：从 $1$ 至 $n$（横坐标的值）每次加上 $k$（$k$ 每次加 $1$），得到的值，为纵坐标的值，这个坐标则 Bessie 一定输的点。

Part 3 发现一个 Bug

还有一个问题：怎么确定横坐标的值，毕竟横坐标并不是从 $1$ 到 $n$ 按顺序的。

考虑在同一行内，至多会有一个红格子 $B$。原因：

• 当这个格子 $A$ 在红格子 $B$ 左边时，一定可以找到从这个格子一步走到另一个红格子 $C$ 的方法，那么 Bessie 从先手变成了后手，而红格子意味着后者会赢，所以这个格子 $A$ 是先手赢。
• 当这个格子 $A$ 在红格子 $B$ 的右边时，一定可以先向左走走到红格子 $B$，那么 Bessie 从先手变成了后手，而红格子意味着后者会赢，所以这个格子 $A$ 是先手赢。

既然我们发现的这个规律，由于 $N$ 和 $M$ 在 $1$ ~ $1000000$ 之间，可以开一个一维数组，下标表示横坐标的值，数组值记录的值为对应的纵坐标的值。之后就执行以下操作：

• 当 $f_i$ 还没有对应纵坐标的值的时候，根据规律计算出 $f_i$ 的值，同时把 $f_{f_i}=i$。因为两个点是关于 $y=x$ 对称的。
• 当 $f_i$ 有对应纵坐标的值的时候，直接跳过，因为这一行已经有红色的点了。

然后就可以 $\mathcal{O(1)}$ 查询了。每次有一个起始坐标 $(x, y)$，则判断 $x$ 对应的纵坐标是否为 $y$，如果是，则 Bessie 输，否则则赢。

Part 4 代码

#include <iostream>
using namespace std;

const int N = 1e6 + 7;

int f[(N<<1)+1], t;
// 记得数组开两倍
// 后面 +1 就是一个习惯，毕竟数组的大小开奇数好像会快一点

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
   // 平时写题可以用用，可以增加 cin 和 cout 速度，但是不能用 scanf 和 printf 了
   // 千万注意考试别用，RE 抱蛋两行泪

	for(int k=0, i=1; i<=(int)1e6; i++)
		if(!f[i]) f[i] = i + (++k), f[f[i]] = i;
		
	cin >> t >> t >> t;
   // 读 3 个 t 就是因为 n 和 m 没用，节省变量，反正会覆盖的
	for(int i=1; i<=t; i++) {
		int x, y;
		cin >> x >> y;
		if(f[x] == y) cout << "Farmer John\n";
		else cout << "Bessie\n";
	}
}

泥们是不是要感谢一下我这个良心题解，没有泥们看不懂的东西，要公式去别的题解看就好了，求赞。