自动搬运

查看原文

来自洛谷，原作者为

	ケロシ Blue Archive

搬运于2025-08-24 21:44:29，当前版本为作者最后更新于2024-11-14 17:04:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

提供一种复杂度正确的算法。

因为穿过一条边的链只有一条，所以考虑 dp 记录这条链的信息，设 $f_{u,k} ~ (k \in subtree(u))$，表示经过 $u$ 以及其父亲的链的底端是点 $k$，不计这条链的最小代价。

不难发现链穿过点 $u$ 的方式有两种，分别是一段连到父亲和不连到父亲：

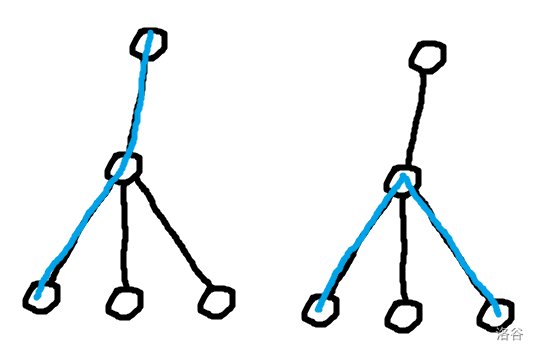
考虑分别进行转移。

考虑在 $u$ 点断掉的链的贡献， 设儿子 $v$ 的贡献为 $g_{v}=\min (f_{v,k}+(d_u-d_k)^2)$，再考虑穿过 $u$ 的链的贡献。

如果穿过点 $u$ 的链连到父亲，其转移：

$f_{u,k}=\sum g + \min_{v\in son(u)} (f_{v,k}-g_v)$

如果穿过点 $u$ 的链不连到父亲，其转移：

$f_{u,u}=\sum g + \min_{v_1,v_2 \in son(u), v_1\ne v_2} (f_{v_1,l}+f_{v_2,r}-g_{v_1}-g_{v_2}+(2d_u-d_l-d_r)^2)$

最后如果根节点度数大于 $1$，则只有 $f_{rt,rt}$ 可以贡献答案，反之 $f_{rt,k}$ 都可以贡献。

这里时间复杂度均摊 $O(n^2)$，考虑优化。

先看 $g_{v}=\min (f_{v,k}+(d_u-d_k)^2)$，如何快速求这个东西。发现贡献是平方形式，考虑各种关于斜率的优化，先把式子拆一下：

$f_{v,k}+(d_u-d_k)^2=f_{v,k}+d_k^2-2d_ud_k+d_u^2$

$(2d_u-d_l-d_r)^2=(2d_u-d_l)^2-2d_r(2d_u-d_l)+d_r^2$

不难想到把 $d_u$ 固定掉，变为一根一次函数，斜率为 $-2d_u$，然后用数据结构查询，比如凸包，这里使用李超线段树。

考虑将所有的 $f_{u,k}$ 插进点 $u$ 的李超树，对于求 $g_u$，直接在李超树查询即可。

对于 $f_{u,k}=\sum g + \min_{v\in son(u)} (f_{v,k}-g_v)$，不难发现就是对 $f_{v,k}$ 里所有函数的截距全部加上 $\sum g - g_v$，整体打个 tag 即可，然后合并到 $f_{u,k}$ 即可。

这里使用启发式合并，将小的合并到大的李超树上去。

对于求 $f_{u,u}$，不难想到在启发式合并的时候顺便遍历小子树，去查询大子树即可。

时间复杂度 $O(n \log^2 n)$。

const int N = 5e4 + 5;
const int M = 3e6 + 5;
const ll LNF = 1e12 + 128;
int n;
int fi[N], ne[N << 1], to[N << 1], ecnt;
int ru[N], d[N];
struct Line {
	ll k, b;
} p[N]; int cnt;
int ls[M], rs[M], F[M], tot;
vector<int> e[N]; int id[N], rt[N];
ll b[N], g[N];
ll sq(ll x) {
	return x * x;
}
ll calc(ll i, ll x) {
	return p[i].k * x + p[i].b;
}
void push(int & u, int l, int r, int x) {
	if(! u) u = ++ tot;
	int mid = l + r >> 1;
	int & y = F[u];
	if(calc(x, mid) < calc(y, mid)) swap(x, y);
	if(l == r) return;
	if(calc(x, l) < calc(y, l)) push(ls[u], l, mid, x);
	if(calc(x, r) < calc(y, r)) push(rs[u], mid + 1, r, x);
}
ll query(ll u, int l, int r, int p) {
	if(! u) return LNF;
	ll res = calc(F[u], p);
	if(l == r) {
		return res;
	}
	int mid = l + r >> 1;
	if(p <= mid) chmin(res, query(ls[u], l, mid, p));
	else chmin(res, query(rs[u], mid + 1, r, p));
	return res;
}
void add(int u, int v) {
	ne[++ecnt] = fi[u];
	to[ecnt] = v;
	fi[u] = ecnt;
}
void dfs(int u, int fa) {
	if(u != 1 && ru[u] == 1) {
		p[u] = {- 2 * d[u], sq(d[u])};
		push(rt[u], 1, n << 1, u);
		e[id[u]].push_back(u);
		return;
	}
	ll res = 0;
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		d[v] = d[u] - 1;
		dfs(v, u);
		g[v] = query(rt[v], 1, n << 1, d[u]) + sq(d[u]) + b[v];
		res += g[v];
	}
	p[u].b = LNF; p[u].k = - 2 * d[u];
	for(int i = fi[u]; i; i = ne[i]) {
		int v = to[i];
		if(v == fa) continue;
		int pos = v;
		b[v] += res - g[v];
		if(SZ(e[id[v]]) > SZ(e[id[u]])) {
			swap(id[u], id[v]);
			swap(rt[u], rt[v]);
			swap(b[u], b[v]);
		}
		for(int x : e[id[v]]) {
			int val = 2 * d[u] - d[x];
			chmin(p[u].b, query(rt[u], 1, n << 1, val) + b[u] + sq(val) - res + p[x].b + b[v] - sq(d[x]));
		}
		for(int x : e[id[v]]) {
			p[x].b += b[v] - b[u];
			push(rt[u], 1, n << 1, x);
			e[id[u]].push_back(x);
		}
	}
	e[id[u]].push_back(u);
	p[u].b -= b[u];
	p[u].b += sq(d[u]);
	push(rt[u], 1, n << 1, u);
}
void solve() {
	cin >> n;
	REP(_, n - 1) {
		int u, v;
		cin >> u >> v;
		add(u, v), add(v, u);
		ru[u] ++, ru[v] ++;
	}
	FOR(i, 1, n) id[i] = i;
	p[0] = {0, LNF};
	d[1] = n;
	dfs(1, 0);
	if(ru[1] == 1) {
		ll ans = LNF;
		FOR(i, 1, n) chmin(ans, p[i].b + p[i].k * d[1] + sq(d[1]) + b[1]);
		cout << ans << endl;
	}
	else {
		cout << p[1].b - sq(d[1]) + b[1] << endl;
	}
}