[USACO10JAN] Shipping Around an Island G

0
15011418730 LV 7 @ 2025-8-24 21:44:00
自动搬运

查看原文

来自洛谷，原作者为

Rigel
苍山负雪，明烛天南。|| 高二现役 OIer。

搬运于2025-08-24 21:44:00，当前版本为作者最后更新于2024-05-23 17:58:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

在一个二维平面上，分布着水（ $\texttt{.}$ ）、大陆（ $\texttt{A}$ ）与小岛（ $\texttt{x}$ ）。现要求一条长度最短的环线路线（起点与终点在同一位置），它应满足：
1. 这条路线经过的每一个格子只能是水（ $\texttt{.}$ ）。
2. 这条环线路线的内部应包括整个大陆（ $\texttt{A}$ ）。
3. 这条环线路线的内部不应包括任一小岛（ $\texttt{x}$ ）。
此外，我们规定这条路线可以多次经过同一个格子。也就是说，路线可以重叠。求这条路线的长度，即这条路线经过格子的个数（数据保证有解）。

例如下图，这条红色的路线是不合法的（路线内部包括了一个小岛 $\texttt{x}$ ）。

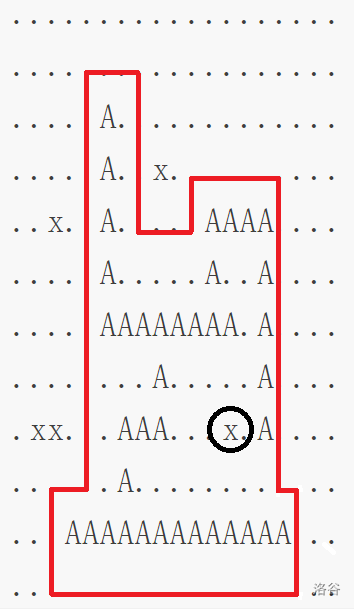
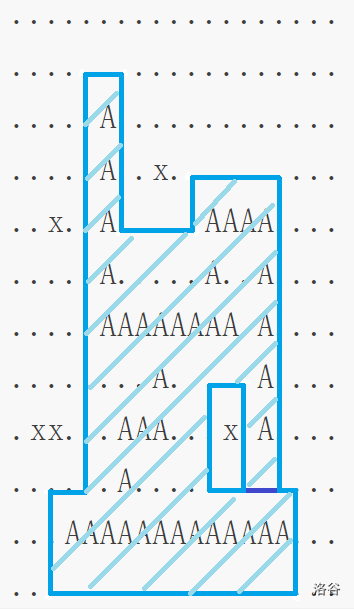
如下图，这条蓝色的路线是合法的（图中深蓝色表示路径重叠部分，阴影部分表示环线路线的内部）。

思路

染色

简而言之，这道题的本质就是染色。

染色在本题中体现为将一些水（ $\texttt{.}$ ）染色成为大陆（ $\texttt{A}$ ）。染色完毕后，只需求出整个大陆的周长即可。于是，如何染色成为了本题的重难点。

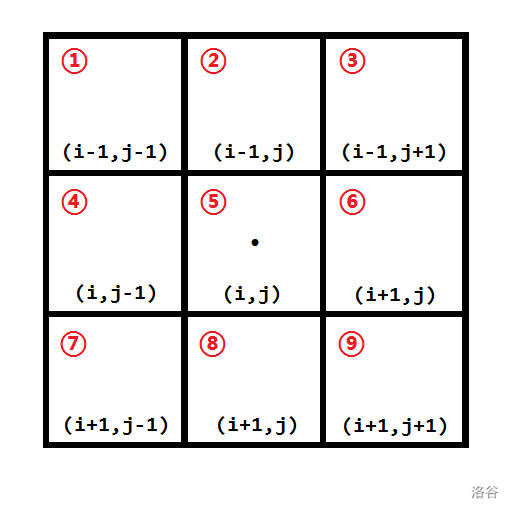
对于每一个水格子（ $\texttt{.}$ ）是否应该被染色，我们从以这个格子为中心的 $3\times 3$ 方格来考虑。为简单起见，我们考虑如下图所示定义以水格子 $(i,j)$ 为中心的 $3\times 3$ 方格：

当 $(i,j)$ 不是水（ $\texttt{.}$ ）时，直接跳过该点；当 $(i,j)$ 是水时，分以下几种情况讨论：
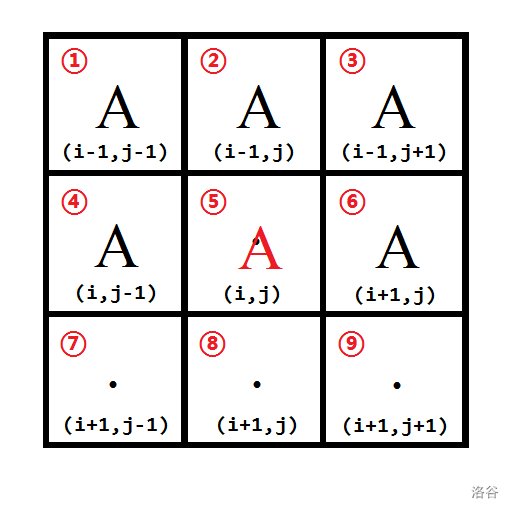
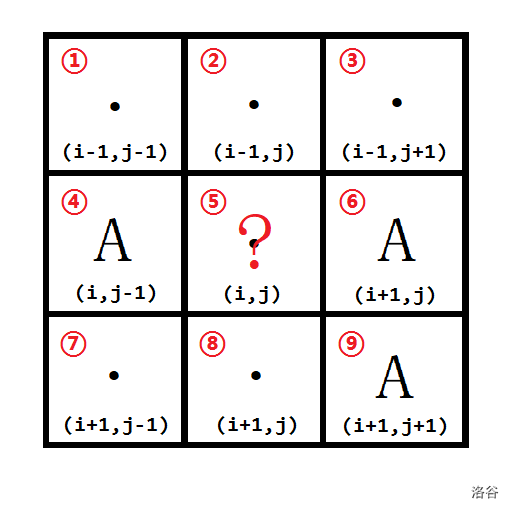
1. 当格子 $2$ 、 $4$ 、 $6$ 、 $8$ 中有大于等于三个格子是大陆（ $\texttt{A}$ ）时，直接将 $(i,j)$ 染色为 $\texttt{A}$ ，因为最短的路不可能走到这里。例如下图，格子 $2$ 、 $4$ 、 $6$ 为 $\texttt{A}$ ，因此格子 $5$ 也被染成 $\texttt{A}$ 。
1. 当格子 $2$ 、 $4$ 、 $6$ 、 $8$ 中恰好有两个格子是大陆（ $\texttt{A}$ ）时，且这两个 $\texttt{A}$ 分别位于格子 $5$ 的两侧，则这个格子暂时不填。例如下图，格子 $4$ 、 $6$ 为 $\texttt{A}$ 。若将格子 $5$ 填上，则格子 $1$ 、 $2$ 、 $3$ 向外延伸的水连通块与格子 $7$ 、 $8$ 向外延伸的水连通块有可能会被互相隔绝。
在下图的情况下，中间的格子是不能被填上的。因为如果填上了，会把里面的 $\texttt{x}$ 与外界隔绝，是不合法的。

在下图的情况下，中间的格子之后会被自下而上地重新搜到而填充上色，因为下面的格子之后会被染色。

因此，我们在将任一格子填充之后，必须重新判断这个格子周围一圈（八个）格子的情况并讨论其是否需要填充上色。
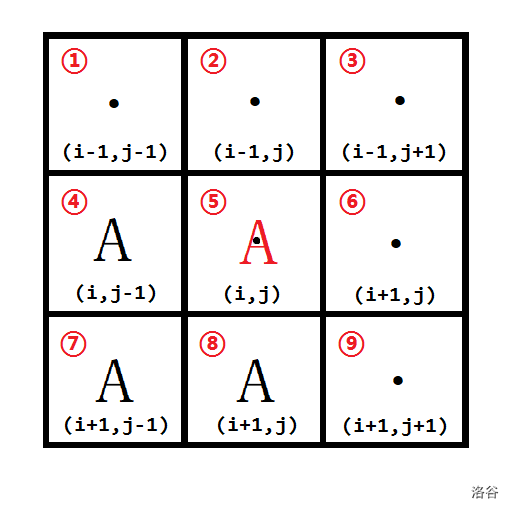
1. 当格子 $2$ 、 $4$ 、 $6$ 、 $8$ 中恰好有两个格子是大陆（ $\texttt{A}$ ）时，且这两个 $\texttt{A}$ 格子的顶点相邻（例如格子 $2$ 、 $4$ 或格子 $4$ 、 $8$ ），则分以下两种情况讨论：
（1）当格子 $5$ 填上后，会把这个 $3\times 3$ 方格中剩余的水格子分割成独立的两块，则这个点暂时不填，理由同第二种情况。例如下图，顶点相邻的格子 $4$ 、 $8$ 为 $\texttt{A}$ ，若将格子 $5$ 填上，则可能会把格子 $1$ 、 $2$ 向外延伸的水连通块与格子 $6$ 、 $9$ 向外延伸的水连通块相互隔绝。

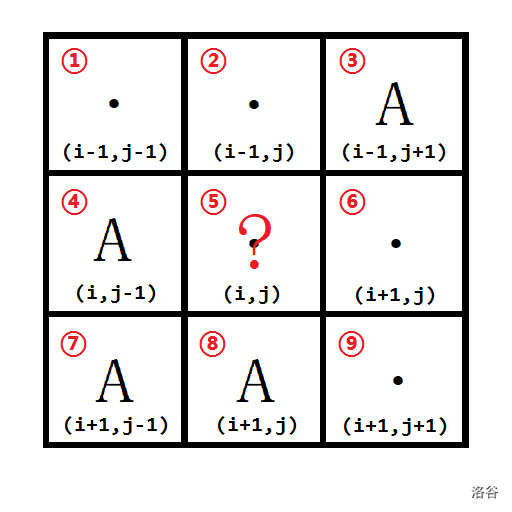
需要注意的是，隔绝水格子的不只是大陆（ $\texttt{A}$ ），也有可能是小岛（ $\texttt{x}$ ）。

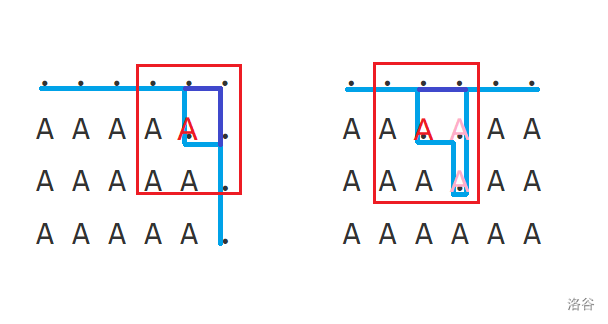
（2）当格子 $5$ 填上后，不会把这个 $3\times 3$ 方格中剩余的水格子分割成独立的两块，则这个点直接填上。例如下图，顶点相邻的格子 $4$ 、 $8$ 为 $\texttt{A}$ ，我们将格子 $5$ 直接填上。

这种类型的格子直接填上的原因是：填上之后只有好处没有坏处。如左下图，填上之后路径长度没有改变；如右下图，填上之后会导致右边两个粉色的格子之后也被填上，最终路径长度缩短。换句话说，填这种类型的格子对路径有截弯取直的作用。
1. 当格子 $2$ 、 $4$ 、 $6$ 、 $8$ 中只有小于等于一个格子是大陆（ $\texttt{A}$ ）时，这个格子暂时不填，同理，如有需要之后会重新搜回来。
按这种方式处理完所有格子之后，我们直接求一遍所得大陆的周长即可得出答案。

如下是样例染色前与染色后的对比。
```
................... 
................... 
.....A............. 
.....A..x.......... 
..x..A.....AAAA.... 
.....A.....A..A.... 
.....AAAAAAAA.A.... 
........A.....A.... 
.xx...AAA...x.A.... 
......A............ 
...AAAAAAAAAAAAA... 
................... 
```
```
...................
...................
....AAA............
....AAA.x..........
..x.AAA...AAAAA....
....AAAAAAAAAAA....
....AAAAAAAAAAA....
....AAAAAAA...A....
.xx.AAAAAAA.x.A....
....AAAAAAA........
...AAAAAAAAAAAAA...
...................
```
求大陆周长

我们采用常规思路：从第一次出现的大陆（ $\texttt{A}$ ）的上面一格为起点开始走出第一步，紧贴大陆顺时针走一圈，并统计走过的格子个数。

假设上一步的方向为向右，则这一步应优先向下，因为我们需要紧贴大陆走一圈；如果无法往下，则应尝试向右；如果还是不行，则应向上（我们规定第一步的上一步方向为向右）。

如下图，分别给出了当上一步（红色）为向右时，这一步（蓝色）分别向右、向上、向下时的情况。

同理，我们可得：若上一步的方向为 $\theta$ （其中 $\theta$ 满足该方向所代表的射线绕原点顺时针旋转 $\theta$ 之后恰与 $x$ 轴正半轴重合），则下一步应优先向 $\theta-90\degree$ （右转），若不行则向 $\theta$ （直行），再不行则向 $\theta+90\degree$ （左转），其中角度按模 $360\degree$ 计。

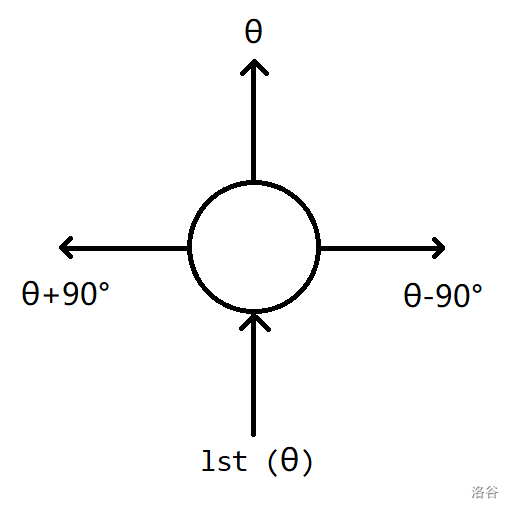
按此方法一直走，并记录经过的格子个数，直到走回起点。

代码实现 & 完整代码

由于这道题考察的主要是思维，且每个人的代码习惯不一，我会给出我的完整代码和注释，而不是每一步的具体实现方法。
```
#include<bits/stdc++.h>
#define int long long
#define maxn 1010
using namespace std;
int n,m,ans;
int d[10][2]={{-1,0},{-1,-1},{0,-1},{1,-1},{1,0},{1,1},{0,1},{-1,1}};
int f[5][2]={{0,1},{1,0},{0,-1},{-1,0}};
char c[maxn][maxn];
inline int read(){
	int ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')ret=ret*10+(ch&15),ch=getchar();
	return ret*f;
}
inline char GC(){
	char ch=getchar();
	while(ch!='.'&&ch!='A'&&ch!='x')ch=getchar();
	return ch;
}
bool check(int x,int y){ // 判断一个点是否在地图范围之内
	return (x>=1&&y>=1&&x<=n&&y<=m);
}
void color(int x,int y){ // 染色函数
	if(c[x][y]!='.')return; // 若当前格子不是水，直接跳过
	int cnt_A=0,cnt_x=0; // 统计该格子周围 A 的数量与 x 的数量
	for(int i=0;i<=3;i++){
		int xx=x+f[i][0],yy=y+f[i][1];
		if(!check(xx,yy))continue;
		cnt_A+=(c[xx][yy]=='A');
	}
	for(int i=0;i<=7;i++){
		int xx=x+d[i][0],yy=y+d[i][1];
		if(!check(xx,yy))continue;
		cnt_x+=(c[xx][yy]=='x');
	}
	int chk=0; 
	for(int i=0;i<=3;i++){
		if(c[x+f[i][0]][y+f[i][1]]=='A'&&c[x+f[(i+1)%4][0]][y+f[(i+1)%4][1]]=='A'&&c[x+f[(i+2)%4][0]][y+f[(i+2)%4][1]]=='.'&&c[x+f[(i+3)%4][0]][y+f[(i+3)%4][1]]=='.'){
            // 情况 3.
			chk=i+1;
			break;
		}
	}
	if((chk==1&&c[x-1][y-1]!='.')||(chk==2&&c[x-1][y+1]!='.')||(chk==3&&c[x+1][y+1]!='.')||(chk==4&&c[x+1][y-1]!='.'))chk=0; 
  	// 情况 3.(1)
	if((chk&&(!cnt_x))||cnt_A>=3){ // 情况 1. 或 3.(2)
		c[x][y]='A';
		for(int i=0;i<=7;i++){
			int xx=x+d[i][0],yy=y+d[i][1];
			if(!check(xx,yy))continue;
			color(xx,yy); // 染色之后要重新判断周围格子的情况
		}
	}
    // 情况 2. 与 4. 均不满足染色条件
}
void calc(int x,int y){ // 计算大陆周长
	int nx=x,ny=y,opt=0; // opt 为上一步方向编号
	do{
		for(int i=5;i>=3;i--){ // 按优先级尝试走每一个方向（i 取 5 至 3 是为了避免下标出现负数）
			int xx=nx+f[(opt+i)%4][0],yy=ny+f[(opt+i)%4][1];
			if(c[xx][yy]=='.'){
				nx=xx,ny=yy;
				opt=(opt+i)%4; // 更新方向编号
				break;
			}
		}
		ans++; // 记录经过的格子总数
	}while(!(nx==x&&ny==y));
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)c[i][j]=GC();
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)color(i,j); // 尝试对每一个格子做染色操作
	int chk=1;
	for(int i=1;i<=n&&chk;i++){
		for(int j=1;j<=m&&chk;j++){
			if(c[i][j]=='A'){
				calc(i-1,j); // 从第一次出现的 A 的上面一格开始计算大陆周长
				chk=0;
			}
		}
	}
	printf("%lld\n",ans);
	return 0;
}
```
本文参考了题解1和题解2。但其年代久远，有些地方没有讲清楚。这篇题解给出了更清楚的解题思路。