自动搬运

查看原文

来自洛谷，原作者为

	QQQfy **

搬运于2025-08-24 21:43:37，当前版本为作者最后更新于2019-02-07 20:33:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

分层图板子题

1.闲聊&写作目的

本蒟蒻的第二篇题解

很久以前就想学分层图了，但一直找不到易于理解的教程（我太弱了）

本文旨在为和我一样弱的蒟蒻们提供良好的体验

与子共食

2.什么是分层图？

嘛，就是形如

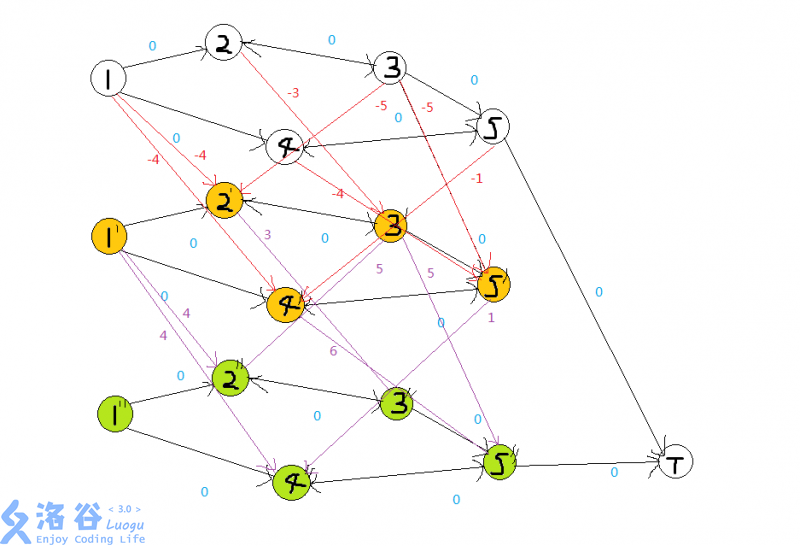
的一个东西。（图自P1073@fy1234567ok的题解，侵删）

啊！好珂怕！

然而它与普通图也并没有什么区别。我们发现，上图的三层图，其形态结构几乎一样，所不同的只是图之间的联系罢了。可以理解为把每一个点拆成多个点变成的多层的图。

好！那么分层图中的边有什么意义吗？

3.分层图的意义？

分层图中的边权可以随着题目的改变而具备不同的意义。在本题中，边权的定义是：

1.当边 <u,v,w> 位于第i层上时，表示已改建了i条道路，且不改建当前道路，由u向v耗费w

2. 当边 <u,v,w> 位于第i层与i+1层时，表示已改建了i条道路，且改建当前道路，由u向v耗费w

在本题中，1中的边与原图的边没有区别，而2中的边权显然为0.

好像很有道理，但它是怎么解决本题的呢？

由于本题求的是1到n的最短路，由于1到n能改建0到k中的任意次道路，再联系定义，得

ans=min（ans，dist[i]），其中i为1到n

dist数组记得开maxk* maxn（因为有k层图鸭）

那么分层图能够解决什么类型的问题呢？

4.分层图的应用范围

并没有

大概是把一张图进行k次修改（本题），或者是改变图的定义使其满足本特点的问题（P1073）

5.代码实现

据说本题卡spfa

数组开大点不然紫一半

#include<bits/stdc++.h>
using namespace std;

const int maxn=100100;
const int maxm=500500;

int nextt[maxm*42],w[maxm*42],to[maxm*42],head[maxn*42],cnt=0;

void add(int u,int v,int cost)
{
	cnt++;
	nextt[cnt]=head[u];
	head[u]=cnt;
	to[cnt]=v;
	w[cnt]=cost;
}

struct node
{
	int u,dis;
	bool operator<(const node x) const
	{
		return dis>x.dis;
	}
};

priority_queue<node> q;
int dist[maxn*21];

void dij(int s)
{
	memset(dist,0x3f,sizeof(dist));
	dist[s]=0;
	q.push((node){s,0});
	while (!q.empty())
	{
		node fr=q.top();q.pop();
		int u=fr.u,dis=fr.dis;
		if (dis!=dist[u]) continue;
		for (int v=head[u];v;v=nextt[v])
			if (dist[to[v]]>dist[u]+w[v])
			{
				dist[to[v]]=dist[u]+w[v];
				q.push((node){to[v],dist[to[v]]});
			}
	}
}

int n,m,k;

int main()
{
	cin>>n>>m>>k;
	for (int i=1;i<=m;i++)
	{
		int u,v,cost;
		cin>>u>>v>>cost;
		add(u,v,cost);add(v,u,cost);
		for (int j=1;j<=k;j++)
		{
			add(n*j+u,n*j+v,cost);add(n*j+v,n*j+u,cost);
			add(n*(j-1)+u,n*j+v,0);add(n*(j-1)+v,n*j+u,0);
		}
	}
	dij(1);
	int ans=dist[n];
	for (int i=1;i<=k;i++)
	{
//		cout<<"### dist["<<i*n+n<<"]: "<<dist[i*n+n]<<endl;
		ans=min(ans,dist[i*n+n]);
	}
	cout<<ans;
	return 0;
}

6. 骗赞

看我妖精军师这么可爱就给点赞呗